第12章 二次根式 复习课件PPT

这是一份第12章 二次根式 复习课件PPT，共15页。

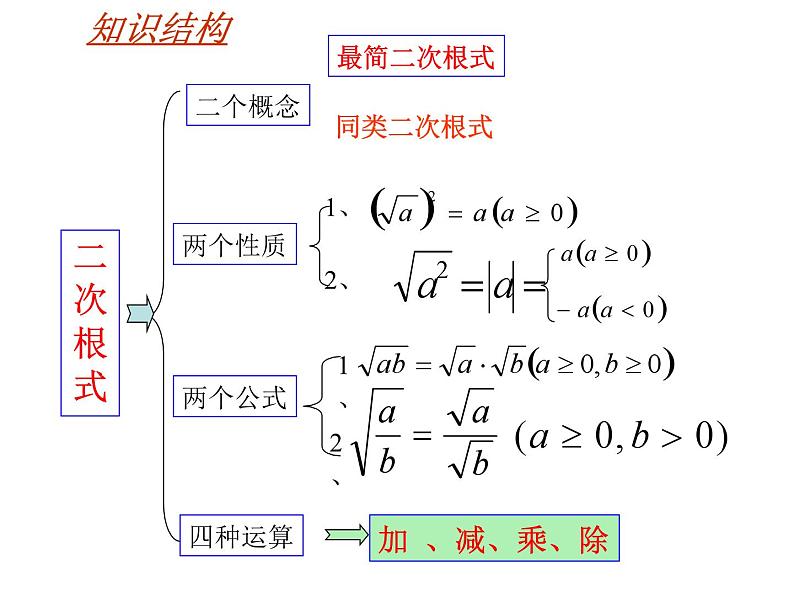
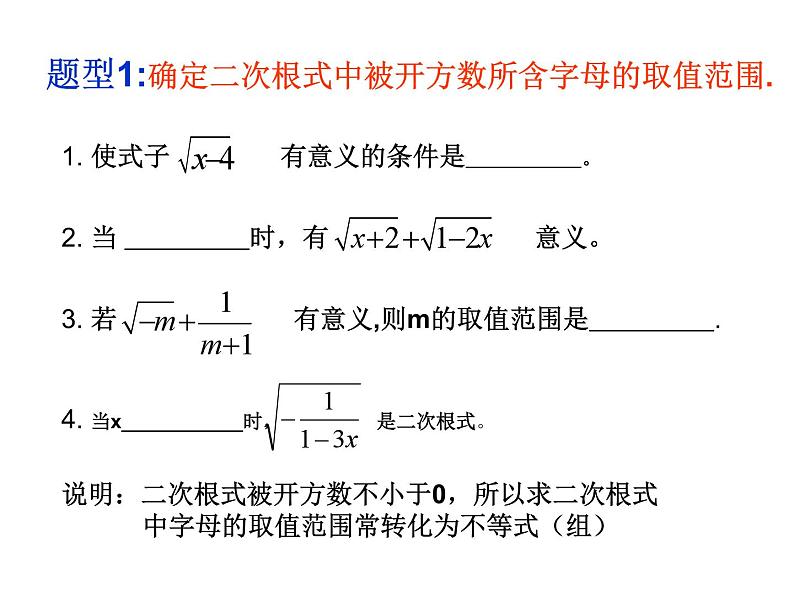
第12章 二次根式 复 习 (一) 学习目标1、能够比较熟练应用二次根式的性质进行 化简.2、能熟练地进行二次根式的运算.3、会运用二次根式的性质及运算解决简单 的实际问题. 二 次 根 式最简二次根式知识结构同类二次根式二次根式的概念形如　　（a　 0）的式叫做二次根式１．二次根式的定义：２．二次根式的识别：（１）被开方数 （２）根指数是２例．下列各式中那些是二次根式？ 那些不是？为什么？⑧⑦⑥⑤④①②③３．二次根式的性质（1）．（2）．（3）．题型1:确定二次根式中被开方数所含字母的取值范围.2. 当 时，有 意义。3. 若 有意义,则m的取值范围是 .4. 当x___________时， 是二次根式。说明：二次根式被开方数不小于0，所以求二次根式 中字母的取值范围常转化为不等式（组） 题型2:二次根式的非负性的应用.4.二次根式性质及运算律（1) · ＝ （a≥0，b≥0），反之 = · （a≥0，b≥0）（2） = （a≥0，b>0），反之 = （a≥0，b>0） (1)二次根式的加减法：5.二次根式的应用通常先把各个二次根式化成最简二次根式，在合并同类二次根式 题型1：化简下列各式(1) +(-3 )2 (2) ÷ · (3) -( -3 )(4)( -3)(2 +1)题型2：计算下列各题，并概括二次 根式运算的一般 步骤 (1) (2) (3) (4) ÷ 三、堂内小结1．本节课复习的五个基本问题是“二次根式”这一章的主要基础知识，同学们要深刻理解并牢固掌握．2．在二次根式的化简、计算及求值的过程中，应注意 利用题中的使二次根式有意义的条件(或题中的隐含 条件)，即被开方数为非负数，以确定被开方数中的 字母或式子的取值范围．3．运用二次根式的基本性质进行二次根式运算时，要 注意论述每一条性质中字母取值范围的条件．4．通过例题的讨论，要学会综合、灵活运用二次根式 的意义、基本性质和法则以及有关多项式的因式分 解，解答有关含二次根式的式子的化简、计算及求 值等问题．