第6章 图形的相似复习课件

这是一份第6章 图形的相似复习课件，共11页。

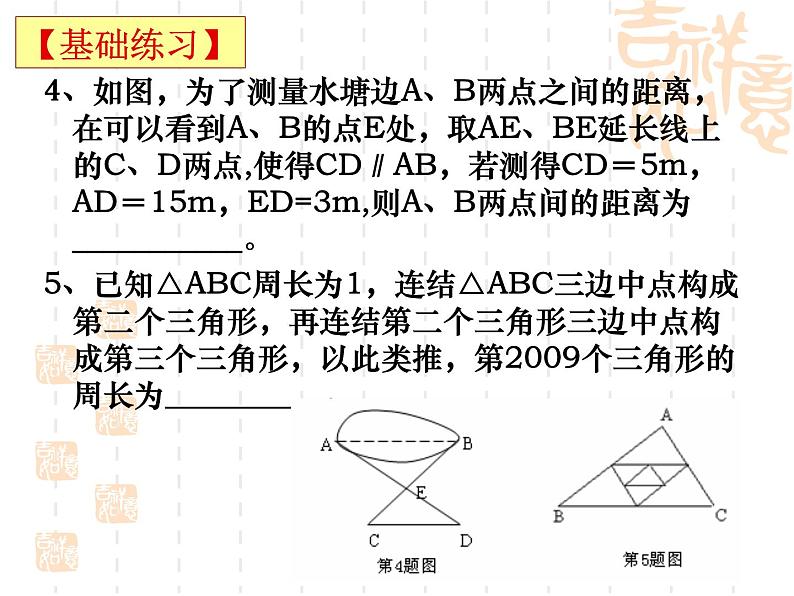
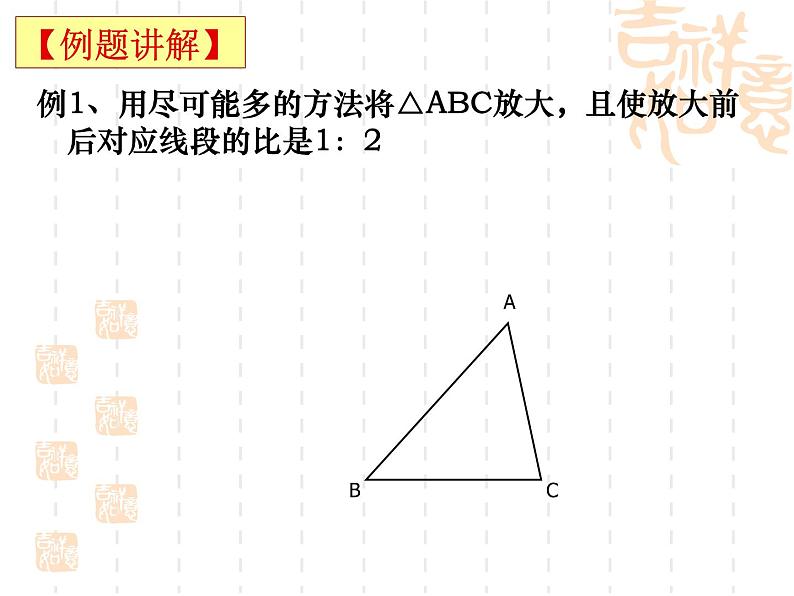
图形的相似复习(2)1、图形的位似，位似变换，平行投影，中心投 影的概念； 2、相似三角形的条件与性质的综合应用。【要点再现】学科网1、用位似图形的方法，可以将一个图形放大或缩小，位似中心的位置可以选在( ) A．原图形的外部 B．原图形的内部 C．原图形的边上 D．任意位置2、图中的两个三角形是位似图形，它们的位似中心是（ ） A.点P B.点O C.点M D.点N3、一棵高3米的小树影长为4米，同时临近它的一座楼房的影长是24米，这座楼房高 米。【基础练习】学科网4、如图，为了测量水塘边A、B两点之间的距离，在可以看到A、B的点E处，取AE、BE延长线上的C、D两点,使得CD∥AB，若测得CD＝5m，AD＝15m，ED=3m,则A、B两点间的距离为___________。5、已知△ABC周长为1，连结△ABC三边中点构成第二个三角形，再连结第二个三角形三边中点构成第三个三角形，以此类推，第2009个三角形的周长为 。 【基础练习】例1、用尽可能多的方法将△ABC放大，且使放大前后对应线段的比是1：2ABC【例题讲解】学科网例2、如图，零件的外径为16cm，要求它的壁厚x，需要先求出内径AB，现用一个交叉钳(AD与BC相等)去量，若测得OA:OD=OB:OC=3:1，CD＝5cm，则零件的壁厚x为 。 【例题讲解】例3、如图，在正△ABC中，已知AB＝BC＝CA＝4cm，AD⊥BC于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x(s)。⑴ 求当x为何值时，PQ⊥AC？当x为何值时，PQ⊥AB？当x为何值时，PQ∥AC？⑵ 设△PQD的面积为y(cm2)，当0＜x＜2时，求y与x的函数关系式；⑶ 当0＜x＜2时，求证：AD平分△PQD的面积。 【例题讲解】1、如图，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷。经过了解，教学楼、水塔的高分别为20m和30m，它们之间的距离为30m，小张身高为1.6m。小张要想看到水塔，他与教学楼的距离至少应有多少m？ 【练习巩固】学科网2、如图，花丛中有一路灯杆AB.在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH＝5米.如果小明的身高为1.7米，求路灯杆AB的高度(精确到0.1米)． 【练习巩固】3、汪老师要装修自己带阁楼的新居，在建造客厅到阁楼的楼梯 AC 时，为避免上楼时墙角F碰头，设计墙角F到楼梯的竖直距离FG为1.75m，他量得客厅高AB= 2.8m，楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.请你帮助汪老师解决下列问题： （1）要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米？（2）在（1）的条件下，为保证上楼时的舒适感，楼梯的每个台阶小于 20cm，每个台阶宽要大于20cm, 问汪老师应该将楼梯建儿个台阶？为什么？ 【练习巩固】4、如图所示，在△ABC中，AB=AC=1，点D、E在直线BC上运动，设BD=x，CE=y．（1）如果∠BAC=30°，∠DAE=105°，试确定y与x之间的函数关系式；（2）如果∠BAC的度数为α，∠DAE的度数为β，当α、β满足怎样的关系式时，（1）中y与x之间的函数关系式还成立，并说明理由。【练习巩固】学科网