高考数学二轮导数专题复习——第二十三节 双变量问题之极值点偏移-原卷版

这是一份高考数学二轮导数专题复习——第二十三节 双变量问题之极值点偏移-原卷版，共1页。试卷主要包含了对数平均不等式等内容，欢迎下载使用。
第二十三节  双变量问题之极值点偏移知识与方法1.设函数在定义域上有极值点，但由于函数在极值点左右两侧的增减速率不对称，造成函数的图象不关于直线对称，那么当时，极值点会偏向或中的某一个，也即或，在给定的函数背景下，证明上面的两个不等式，这类问题称为极值点偏移问题.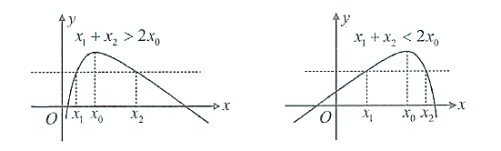2．极值点偏移问题常用的解题方法有三种：（1）构造对称差函数，研究其单调性，证明不等式；（2）通过变形，转化为双变量问题，用齐次换元化归成单变量不等式证明问题；（3）利用对数平均不等式证明.（由于在作答时要先证明此不等式，故一般正式作答时不使用此法）3.对数平均不等式：设，，且，则.典型例题【例1】已知函数（1）求函数的最大值；（2）设，若，证明：.【例2】已知函数，其中.（1）讨论的单调性；（2）若有两个零点，，证明：.强化训练1.已知函数.（1）求的最小值；（2）若关于x的方程有两个不相等的实根，，证明：.2．已知函数.（1）当时，求的单调区间；（2）若的图象与x轴有两个交点，，且，证明：.3.已知函数有两个不同的极值点，（1）求a的取值范围；（2）证明：.