初中华师大版21.3 二次根式的加减教案设计

这是一份初中华师大版21.3 二次根式的加减教案设计，共2页。教案主要包含了知识与技能，过程与方法，情感态度，教学重点，教学难点等内容，欢迎下载使用。
21.3  二次根式的加减※教学目标※【知识与技能】1.知道什么是同类二次根式，会辨别两个根式是否是同类二次根式.2.学会通过合并同类二次根式，进行二次根式的加法与减法运算.3.会进行二次根式的加减混合运算.【过程与方法】1.经历探索二次根式的加减法运算法则过程，培养学生的探究精神和合作交流的习惯.2.体会用类比的思想研究二次根式的加减法运算法则，体验研究数学问题的常用方法：由特殊到一般，由简单到复杂.【情感态度】教学中为学生创造大量的操作、思考和交流的机会，关注学生思考问题的过程，鼓励学生在探索规律的过程中从多个角度进行考虑，品尝成功的喜悦，激发学生应用数学的热情，培养学生主动探索，敢于实践，善于发现的科学精神以及合作精神，树立创新意识.【教学重点】掌握二次根式的加减法运算法则，会用它进行简单的二次根式的加减法运算.【教学难点】经历知识产生的过程，探索新知识及二次根式的混合运算.※教学过程※一、复习引入计算下列各式：二、探索新知1.试计算：教师点拨：（1）如果我们把当成x,不就能转化为上面的问题了吗？（2）把2.通过观察以上两道计算题，你联想到了什么？3.归纳：通过观察，启发我们，类似在整式的加减中合并“同类项”那样，能不能在二次根式的加减中,也合并一种“同类二次根式”呢？（学生讨论类比同类项，得出同类二次根式的概念）4.同类二次根式的特点：①被开方数相同；②二次根式是最简二次根式；③与二次根式前面的“系数”无关.5.怎样判断两个二次根式是不是同类二次根式呢？①先将所给的二次根式化成最简二次根式;②看被开方数是否相同，相同的是同类二次根式，否则不是同类二次根式.【例1】  在下列各组二次根式中，属于同类二次根式的是(    )分析：化简各项可得显然：答案选B.6.二次根式的加减二次根式的加减，与整式的加减相类似，只需对同类二次根式进行合并，合并的方法是：将同类二次根式前面的“系数”进行加减.【例2】  计算：.(先让学生独立完成，教师可适当点拨)解：原式=思考：你会计算：吗？引导学生分析出先将各二次根式化成最简二次根式，再进行加减，最后学生完成解答.【例3】  计算：分析：先化成最简二次根式，再进行加减运算.解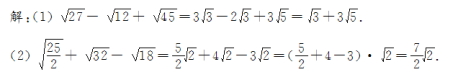：三、巩固练习计算：答案：四、应用拓展【例4】  计算：教师引导学生观察，类比以前的整式乘法的运算，将整式乘法的运算方法迁移到二次根式的运算中来.解：（1）原式=(2)原式=归纳：复杂的二次根式的计算可运用整式乘法的运算法则进行.五、归纳小结1.同类二次根式的特点及判断.2.二次根式的加减的实质就是合并同类二次根式，整式的运算法则在二次根式中仍适用.※课后作业※教材习题21.3第1、2题.选作：教材习题21.3第3题.