第04讲 根据集合之间的关系求参数-2023-2024学年高一数学期末总复习（人教A版必修第一册）

这是一份第04讲 根据集合之间的关系求参数-2023-2024学年高一数学期末总复习（人教A版必修第一册），文件包含第4讲根据集合之间的关系求参数解析版docx、第4讲根据集合之间的关系求参数原卷版docx等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。
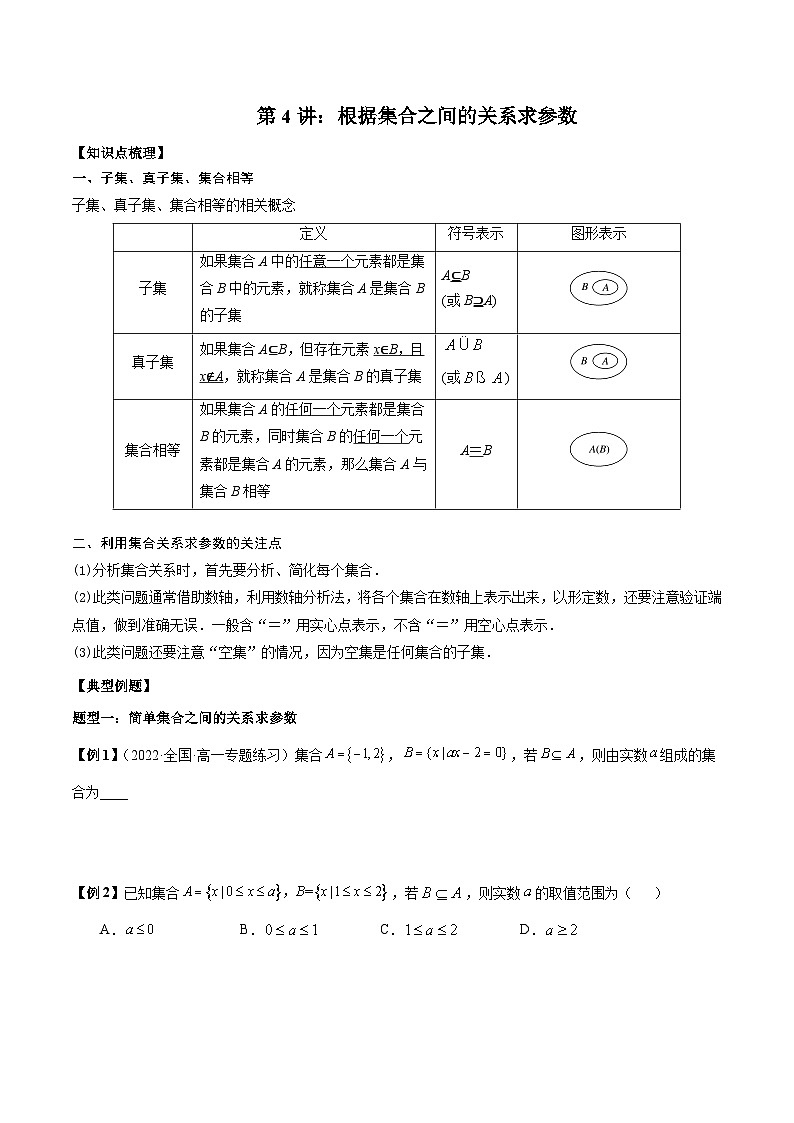
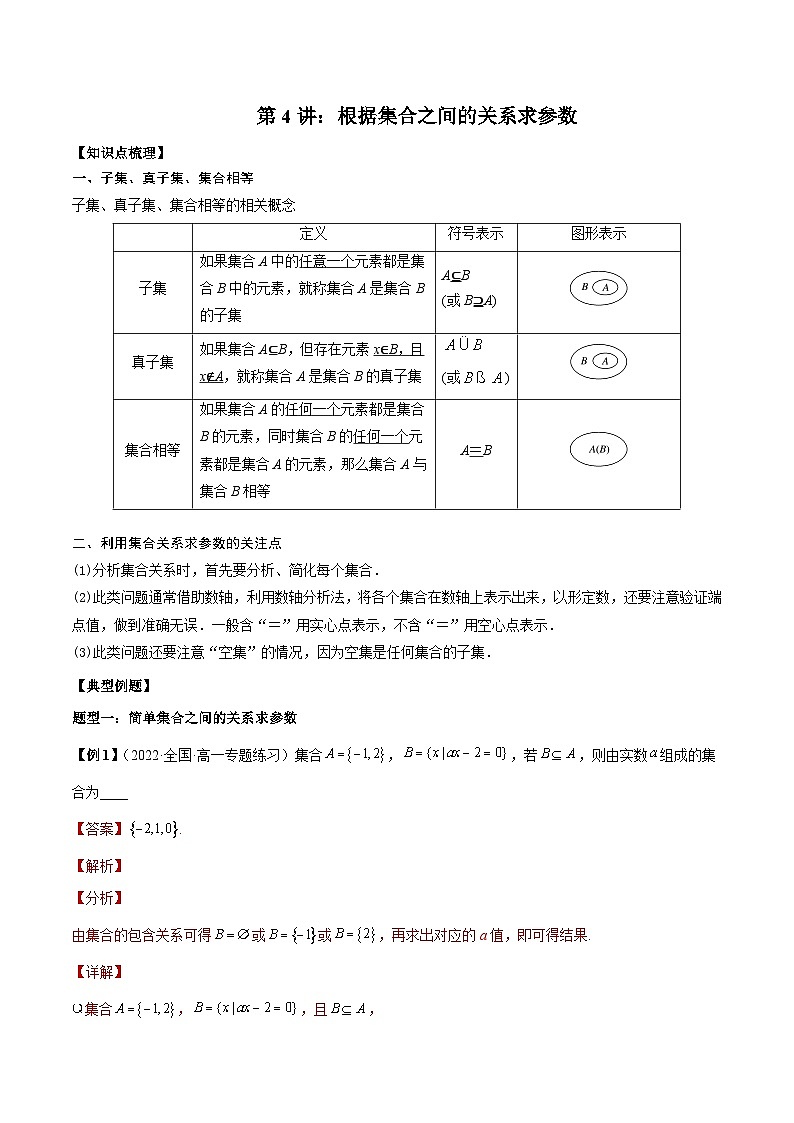
第4讲：根据集合之间的关系求参数
【知识点梳理】
一、子集、真子集、集合相等
子集、真子集、集合相等的相关概念

定义
符号表示
图形表示
子集
如果集合A中的任意一个元素都是集合B中的元素，就称集合A是集合B的子集
A⊆B
(或B⊇A)

真子集
如果集合A⊆B，但存在元素x∈B，且x∉A，就称集合A是集合B的真子集

(或)

集合相等
如果集合A的任何一个元素都是集合B的元素，同时集合B的任何一个元素都是集合A的元素，那么集合A与集合B相等
A＝B


二、利用集合关系求参数的关注点
(1)分析集合关系时，首先要分析、简化每个集合．
(2)此类问题通常借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误．一般含“＝”用实心点表示，不含“＝”用空心点表示．
(3)此类问题还要注意“空集”的情况，因为空集是任何集合的子集．
【典型例题】
题型一：简单集合之间的关系求参数
【例1】（2022·全国·高一专题练习）集合，，若，则由实数组成的集合为____
【答案】.
【解析】
【分析】
由集合的包含关系可得或或，再求出对应的a值，即可得结果.
【详解】
集合，，且，
或或，
．则实数组成的集合为.
故答案为：.
【例2】已知集合，若，则实数的取值范围为（ ）
A． B． C． D．
【答案】D
【详解】
因为集合，，
所以.
故选：D
【例3】已知，，，则范围____________.
【答案】
【详解】
(1)当有，此时，解得，符合题意；
(2) 当要使，只需，解得
综上所述，实数的范围是．
故答案为：．
【题型专练】
1．（2021·江苏省沭阳高级中学高一期中）集合，，若，则的值为__________.
【答案】0
【解析】
【分析】
根据集合的包含关系求解，即由求解．
【详解】
因为，所以，
显然，
若，则与集合元素的互异性矛盾，舍去；
若，则或（舍去），
综上，．
故答案为：0．
2.已知集合，则=（ ）
A．或 B．或3 C．1或 D．1或3
【答案】B
【详解】
因为集合，，且，所以或，
若，则，满足；
若，则或，
当时，，满足；
当时，集合A中元素不满足互异性，舍去，
故选：B.
3.已知集合，，若，则（ ）
A．-3 B．-2 C．3 D．-2或3
【答案】C
【详解】
因为，
若，则，，集合中的元素不满足互异性，舍去；
若，则或-2，因为，所以.
故选C.


4.已知集合.若，则实数的取值范围为_________.
【答案】
【详解】
已知集合，且，
当时，，解得，符合题意；
当时，则，解得，
综上：实数的取值范围为.
故答案为：
5.已知，若，则实数的取值范围（ ）
A． B． C． D．
【答案】D
【详解】
由题意，∵，∴．
故选：D．
6.已知集合，，若，则由实数的所有可能的取值组成的集合为（ ）
A． B． C． D．
【答案】D
【详解】
当时，方程没有实数根，故，显然符合，
当时，由，显然，因此要想，
只有，因此实数的所有可能的取值组成的集合为.
故选：D


题型二：先求集合，在利用集合之间的关系求参数
【例1】已知，，若，则实数取值的集合为（ ）
A． B． C． D．
【答案】A
【详解】
因为，
又，
当时，方程无解，则，此时满足；
当时，，此时，为使，只需或，
解得或，
综上，实数取值的集合为.
故选：A.
【例2】已知集合，集合，若，则实数的值是（ ）
A．0 B． C．0或 D．0或
【答案】C
【详解】
，，
当时，，；当时，，；当时，.
即或或.
故选：C.
【例3】已知集合，，若，则实数的取值范围是（ ）
A． B． C． D．
【答案】A
【详解】
由题知，又，
则，解得
故选：A
【例4】已知集合，，若，则实数________.
【答案】或或
【详解】
，且，.
①若，则；
②若，则，或，解得或.
综上所述，或或.
故答案为：或或.
【例5】已知集合，集合，若，则的取值范围为（ ）
A． B．
C． D．
【答案】D
【详解】
解不等式得，
要使，
当集合时，，解得；
当集合时，，解得.
综上：.
故选：D.

【题型专练】
1.若集合，，且，则实数取值的集合为（ ）
A． B． C． D．
【答案】D
【详解】
因为，，，
若，则方程无解，所以满足题意；
若，则，
因为，所以，则满足题意；
故实数取值的集合为.
故选：D.
2.当两个集合中有一个集合为另一一集合的子集时称这两个集合之间构成“全食”，当两个集合有公共元素，但互不为对方子集时称两集合之间构成“偏食”.对于集合，，若与构成“全食”，或构成“偏食”，则的取值集合为___________.
【答案】
【详解】
解：当时，，符合条件；
当时，
即时，，
此时应构成“全食”或；
解得：或；
综上所述：的取值集合为.
故答案为：.
3.已知集合，且.
（1）求集合；
（2）如果集合，且，求的值组成的集合.
【答案】（1）；（2）.
【详解】
（1）因为，直接将代入方程：得，，
所以，方程为，
即，
解得或，
所以，集合；
（2）因为是的子集，分两类讨论：
①当时，，由于空集是任何集合的子集，
所以，，符合题意；
②当，则或，
代入解得，或，
综合以上讨论得，的取值集合为：.