初中数学24.1.1 圆教学设计

这是一份初中数学24.1.1 圆教学设计，共7页。
圆心角和圆周角的关系（第2课时）
一． 教学任务分析
知识与技能：
1．掌握圆周角定理的2个推论的内容. 
2．会熟练运用推论解决问题.
过程与方法
1．培养学生观察、分析及理解问题的能力.
2．在学生自主探索推论的过程中，经历猜想、推理、验证等环节，获得正确学习方式.
情感态度与价值观：培养学生的探索精神和解决问题的能力.
教学重点：圆周角定理的几个推论的应用.
教学难点：理解几个推论的“题设”和“结论”
二． 教学设计分析
第一环节 课前复习
活动内容：
1.求图中角X的度数：

x= x=

2.求图中角X的度数：
∠ABF=20°，∠FDE=30°
x= x=
第二环节 新课学习（一）
活动内容：
（1）观察图，BC是⊙O的直径，它所对的圆周角有什么特点？你能证明吗？
首先，让学生明确，“它所对的圆周角”指的是哪个角？（∠BAC）
然后，让学生猜想，这个角的特点，并拿量角器实际测量，看看猜测是否准确.（∠BAC是一个直角）
最后，让学生自行考虑进行证明的方法.引导应用圆周角和圆心角关系定理进行证明.
解：直径BC所对的圆周角∠BAC=90°
证明：
∵BC为直径
∴∠BOC=180°
∴（圆周角的度数等于它所对弧上的圆心角的度数的一半）
（2）观察图，圆周角∠BAC=90°，弦BC是直径吗？为什么？
首先，让学生猜想结果；
然后，再让学生尝试进行证明.
解：弦BC是直径.
连接OC、OB
∵∠BAC=90°
∴∠BOC=2∠BAC=180°
（圆周角的度数等于它所对弧上的圆心角的度数的一半）
∴B、O、C三点在同一直线上
∴BC是⊙O的一条直径
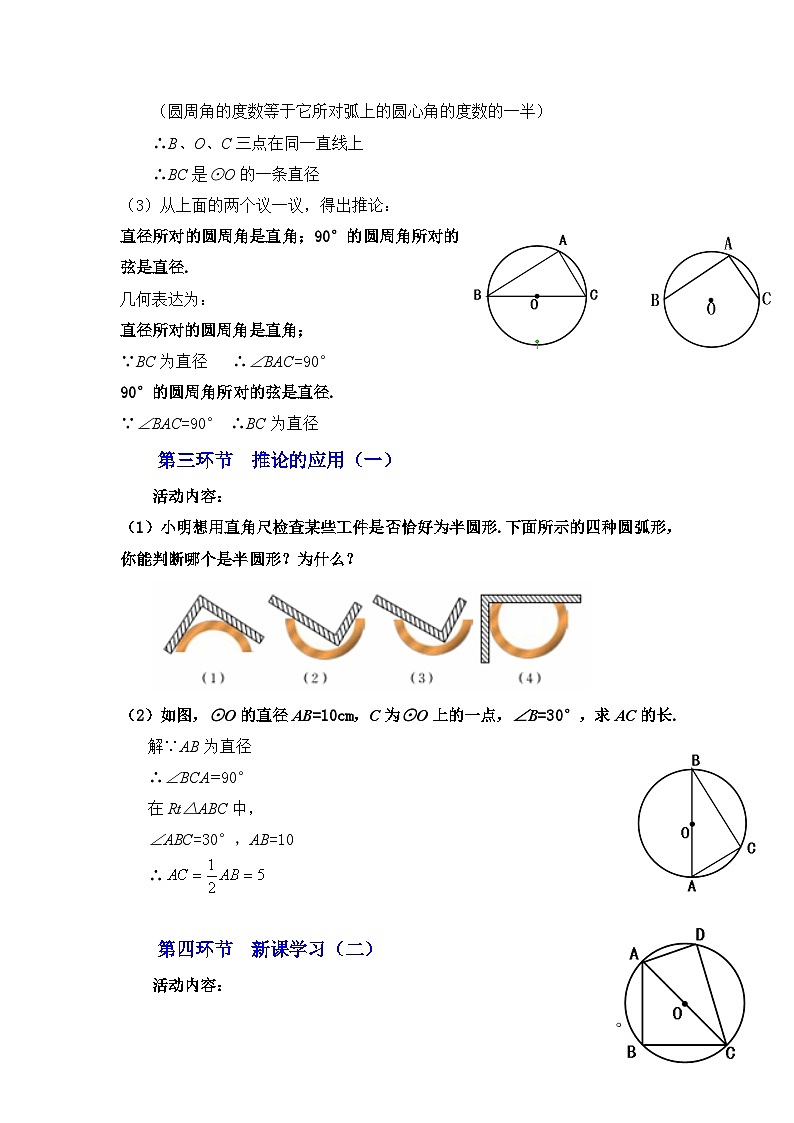
（3）从上面的两个议一议，得出推论：
直径所对的圆周角是直角；90°的圆周角所对的弦是直径.
几何表达为：
直径所对的圆周角是直角；
∵BC为直径 ∴∠BAC=90°
90°的圆周角所对的弦是直径.
∵∠BAC=90° ∴BC为直径
第三环节 推论的应用（一）
活动内容：
（1）小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形，你能判断哪个是半圆形？为什么？

（2）如图，⊙O的直径AB=10cm，C为⊙O上的一点，∠B=30°，求AC的长.
解∵AB为直径
∴∠BCA=90°
在Rt△ABC中，
∠ABC=30°，AB=10
∴

第四环节 新课学习（二）
活动内容：
（一）如图，A，B，C，D是⊙O上的四点，AC为⊙O的直径，请问∠BAD与∠BCD之间有什么关系？为什么？
首先：引导学生进行猜想；
然后：让学生进行证明.
解：∠BAD与∠BCD互补
∵AC为直径
∴∠ABC=90°,∠ABC=90°
∵∠ABC+∠BCD+∠ABC+∠BAD=360°
∴∠BAD+∠BCD=180°
∴∠BAD与∠BCD互补
（二）如图，C点的位置发生了变化，∠BAD与∠BCD之间有的关系还成立吗？为什么？
1
2
首先：让学生猜想结论；
然后：让学生拿出量角器进行度量，实验验证猜想结果；
最后：让学生利用所学知识进行严密证明.
解：∠BAD与∠BCD的关系仍然成立
连接OB，OD
∵,（圆周角的度数等于它所对弧上圆心角的一半）
∵∠1+∠2=360°
∴∠BAD+∠BCD=180°
∴∠BAD与∠BCD互补
（三）圆内接四边形概念与性质探索
如图，两个四边形ABCD有什么共同的特点？
得出定义：四边形ABCD的的四个顶点都在⊙O上，这样的四边形叫做圆内接四边形；
这个圆叫做四边形的外接圆.
通过议一议环节，我们我们发现∠BAD与∠BCD之间有什么关系？
推论：圆内接四边形的对角互补.
几何语言：
∵四边形ABCD为圆内接四边形
∴∠BAD+∠BCD=180°（圆内接四边形的对角互补）
第五环节 推论的应用（二）
活动内容：
如图，∠DCE是圆内接四边形ABCD的一个外角，∠A与∠DCE的大小有什么关系？
让学生自主经历猜想，实验验证，严密证明三个环节
解：∠A=∠CDE
∵四边形ABCD是圆内接四边形
∴∠A+∠BCD=180°（圆内角四边形的对角互补）
∵∠BCD+∠DCE=180°
∴∠A=∠DCE
第六环节 方法小结
活动内容：
议一议：在得出本节结论的过程中，你用到了哪些方法？请举例说明，并与同伴进行交流.
让学生自主总结交流，最后老师再作方法归纳总结.
方法1：解决问题应该经历“猜想——实验验证——严密证明”三个基本环节.
方法2：从特殊到一般的研究方法，对特殊图形进行研究，从而改变特殊性，得出一般图形，总结一般规律.
第七环节 作业布置
随堂练习3.在圆内接四边形ABCD中，∠A与∠C的度数之比为4:5，求∠C的度数.
解：∵四边形ABCD是圆内接四边形
∴∠A+∠C=180°（圆内角四边形的对角互补）
∵∠A:∠C=4:5
∴
即∠C的度数为100°.

习题3.5
1.如图，在⊙O中，∠BOD=80°，求∠A和∠C的度数.
解：∵∠BOD=80°
∴
（圆周角的度数等于它所对弧上的圆心角的度数的一半）
∵四边形ABCD是圆内接四边形
∴∠DAB+∠BCD=180°
∴∠BCD=180°-40°=140°
（圆内接四边形的对角互补）

2.如图，AB是⊙O的直径，∠C=15°，求∠BAD的度数.
（方法一）解：连接BC
∵AB为直径
∴∠BCA=90°
（直径所对的圆周角为直角）
∴∠BCD+∠DCA=90°，∠ACD=15°
∴∠BCD=90°-15°=75°
∴∠BAD=∠BCD=75°（同弧所对的圆周角相等）
（方法二）解：连接OD
∵∠ACD=15°
∴∠AOD=2∠ACD=30°
（圆周角的度数等于它所对弧上的圆心角的度数的一半）
∵OA=OD
∴∠OAD=∠ODA
又∵∠AOD+∠OAD+∠ODA=180°
∴∠BAD=75°

3.如图，分别延长圆内接四边形ABCD的两组对边相交于点E，F，若∠E=40°，∠F=60°,求∠A的度数.
解：∵四边形ABCD是圆内接四边形∴∠ADC+∠CBA=180°
（圆内接四边形的对角互补）
∵∠EDC+∠ADC=180°，
∠EBF+∠ABE=180°
∴∠EDC+ ∠EBF=180°
∵∠EDC=∠F+∠A,∠EBF=∠E+∠A
∴∠F+∠A+∠E+∠A=180°
∴∠A=40°

4.如图，⊙O1与⊙O2都经过A，B两点，且点O2在⊙O1上，点C是弧AO2B上的一点（点C不与A，B重合），AC的延长线交⊙O2于点P，连接AB，BC，BP.
（1）根据题意将图形补充完整；
（2）当点C在弧AO2B上运动时，图中大小不变的角有哪些？（将符合要求的角都写出来）
解：大小不变的角有：
∠ACB
∠APB
∠BCP