





- 3.2 函数的奇偶性与单调性综合习题课课件PPT 课件 1 次下载
- 3.2.1 单调性与最大(小)值1课件PPT 课件 2 次下载
- 3.2.2 函数的奇偶性(1)课件PPT 课件 2 次下载
- 3.2.2 函数的奇偶性(2)课件PPT 课件 1 次下载
- 3.3 幂函数课件PPT 课件 1 次下载
高中人教A版 (2019)第三章 函数概念与性质3.2 函数的基本性质课文配套ppt课件
展开一般地,函数f(x)的定义域为I:
函数的单调性是函数的“局部性质”,它与区间密切相关
特别的,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数
特别的,当函数f(x)在它的定义域上单调递减时,我们就称它是减函数
画出下列函数的草图,并根据图象解答下列问题:
1 说出y=f(x)的单调区间,以及在各单调区间上的单调性;2 指出图象的最高点或最低点,并说明它能体现函数的什么特征?
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值
(1)对于任意的x∈I,都有f(x)≥M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值
2、函数最大(小)值应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M).
1、函数最大(小)值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;
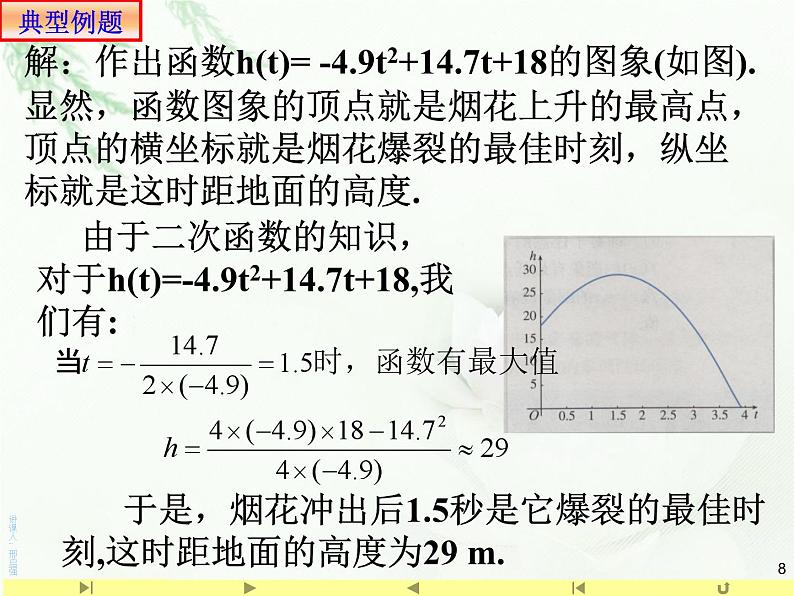
例1、“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂. 如果在距地面高度h m与时间t s之间的关系为:h(t)= -4.9t2+14.7t+18 ,那么烟花冲出后什么时候是它的爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)
解:作出函数h(t)= -4.9t2+14.7t+18的图象(如图).显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由于二次函数的知识,对于h(t)=-4.9t2+14.7t+18,我们有:
于是,烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
解:设x1,x2是区间[2,6]上的任意两个实数,且x1
1.利用二次函数的性质(配方法)求函数的最大(小)值
2. 利用图象求函数的最大(小)值
3.利用函数单调性的判断函数的最大(小)值
如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b) ;
如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b);
求函数的最大(小)值的方法总结:
1、函数f(x)=x2+4ax+2在区间(-∞,6]内递减,则a的取值范围是( )A、a≥3 B、a≤3C、a≥-3 D、a≤-3
2、在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域_______.3、课本第81页第3题
3、课本第81页第3题
例4. 函数y=|x-1|+|x+2|的最小值为 .
练习:课本第86页第4题
人教A版 (2019)必修 第一册3.2 函数的基本性质教案配套课件ppt: 这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质教案配套课件ppt,共19页。PPT课件主要包含了函数单调性的概念,在某区间上,看图说话,4作结论,A单调递减,B单调递增,C一定不单调,D不确定,A1+∞,B-∞1等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文课件ppt,共17页。PPT课件主要包含了单调性,fx1,fx2,fxx2,-∞0,单调性与单调区间,0+∞,几点注意事项,单调性的证明,求单调区间等内容,欢迎下载使用。
人教A版 (2019)必修 第一册2.2 基本不等式背景图课件ppt: 这是一份人教A版 (2019)必修 第一册2.2 基本不等式背景图课件ppt,共42页。PPT课件主要包含了目标认知,上升的,下降的,单调性,单调区间,图3-2-2,图3-2-3等内容,欢迎下载使用。













