北师大版数学 九上 第四章单元测试卷B卷

这是一份北师大版数学 九上 第四章单元测试卷B卷，文件包含答案2docx、原卷docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
北师大版数学 九上 第四章 图形的相似 单元测试卷B卷一．选择题（共36分）1.如图，已知在△ABC纸板中，AC＝4，BC＝8，AB＝11，P是BC上一点，沿过点P的直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么CP长的取值范围是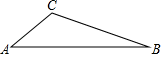（　　）A．0＜CP≤1 B．0＜CP≤2 C．1≤CP＜8 D．2≤CP＜82．如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线于点F，若S△DEC=9，则S△BCF=（　　）A．6 B．8 C．10 D．123.与的相似比为1:3，则与的面积比为（       ）A．1：3 B．1：4 C．1：9 D．1：16 4.如图所示，AB=AC，∠A=36°，AB的中垂线交AC于D，则下列结论：①∠C=72°；②BD平分∠ABC；③△ABD是等腰三角形；④△CBD∽△CAB．正确的个数是（　　）A．1个 B．2个 C．3个 D．4个5．古希腊人认为，最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是（≈0.618，称为黄金分割比例），著名的“断臂维纳斯”雕像便是如此．若某人身材A．160 cm B．170 cm C．180 cm D．190 cm6．已知两个直角三角形的三边长分别为3，4，和6，8，，且这两个直角三角形不相似，则的值为（       ）A．或 B．15 C． D．7．如图，菱形ABCD中，∠BAD=60°，AC、BD交于点O，E为CD延长线上的一点，且CD=DE，连接BE分别交AC，AD于点F、G，连结OG、AE．则下列结论：①OG=AB； ②四边形ABDE是菱形；③；其中正确的是（       ）A．①② B．①③ C．②③ D．①②③8．如图，在正方形中，在边上，在边上，且，过点作，交于点，若，，则的长为（   ）A．10 B．11 C．12 D．139.如图，是的中线，点在上，，连接并延长交于点，则：的值是（    ）A．： B．： C．： D．：10．如图，，且过△ABC的重心，分别与AB，AC交于点D，点E，点F是线段DE上一点，CF的延长线交AB于点G，若DF＝4EF，则S△DFG:S△EFC＝（　　）A．34：9 B．35：8 C．36：7 D．32：711.如图，以点O为位似中心，把△ABC放大为原图形的2倍得到，以下说法中错误的是（       ）A． B．点C，O，在同一直线上C． D．12．如图，在中，，E、F分别是、的中点，延长至D，使，连接、，给出下列结论：①与互相平分，②③，④，⑤平分．正确的有（    ）A．①②③ B．①②④ C．①②③④ D．①②③④⑤二．填空题（共24分） 若，则________．14．如图，△ABC与△是位似图形，点是位似中心，若，，则=________．15.如图，在等边△ABC中，BC＝10，点D是边AB上一点，且BD＝3，点P是边BC上一动点，作∠DPE＝60°，PE交边AC于点E，当CE＝  时，满足条件的点P有且只有一个． 16.如图，将缩小为原来的一半，操作方法如下：任意取一点，连接，取的中点，再连接，，取它们的中点，得到，则与的面积之比是        ．17.如图，在△ABC中，∠C＝90°，BC＝8cm，AB＝10cm，点P从点B出发沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，P，Q两点同时出发，同时停止，经过 _____秒，以C，P，Q为顶点的三角形恰与△ABC相似．18．英国数学家莫雷在1904年发现莫雷角三等分线定理：如图，将任意△ABC的三个内角三等分，每两个内角相邻的三等分线交点D，E，F恰好构成一个正三角形．若△ABC为等腰直角三角形，其中∠BAC=90°，且△ADE的面积为6，则△FBC的面积为________．三．解答题（共60分）19.（8分）如图,在△ABC中,AB=AC，点P在BC上．(1)求作:△PCD,使点D在AC上，且△PCD∽△ABP；(要求:尺规作图，保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC，求证:PD//AB．  20.（8分）如图1，在△ABC中，AB＝BC＝20，cosA＝，点D为AC边上的动点（点D不与点A，C重合），以D为顶点作∠BDF＝∠A，射线DE交BC边于点E，过点B作BF⊥BD交射线DE于点F，连接CF．（1）求证：△ABD∽△CDE；（2）当DE∥AB时（如图2），求AD的长；（3）点D在AC边上运动的过程中，若DF＝CF，则CD＝　 　． 21.（8分）．如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．(1)求证：；(2)如图2，连接AC交BD于O，连接OE，若CE⊥BC，求证：△POC∽△AEC． 22.（8分）如图，在△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE．点M，N分别是BD，CE的中点，连接AM，AN，MN．（1）求证：△CAE≌△BAD；（2）求证：△AMN∽△ABC；（3）若AC＝6，AE＝4，∠EAC＝60°，求AN的长． 23.（8分）（1）发现：如图①所示，在正方形ABCD中，E为AD边上一点，将△AEB沿BE翻折到△BEF处，延长EF交CD边于G点，求证：△BFG≌△BCG．（2）探究：如图②，在矩形ABCD中，E为AD边上一点，且AD＝8，AB＝6．将△AEB沿BE翻折到△BEF处，延长EF交BC边于G点，延长BF交CD边于点H，且FH＝CH，直接写出AE的长． 24.（8分）如图，在△ABC中，点D为BC边的任意一点，以点D为顶点的∠EDF的两边分别与边AB，AC交于点E、F，且∠EDF与∠A互补．（1）如图1，若AB=AC，D为BC的中点时，则线段DE与DF有何数量关系？请直接写出结论；（2）如图2，若AB=kAC，D为BC的中点时，那么（1）中的结论是否还成立？若成立，请给出证明；若不成立，请写出DE与DF的关系并说明理由；（3）如图3，若=a，且=b，直接写出=　 　．   25.（12分）如图（1），等腰三角形中，，．点，分别在，上，．(1)    操作发现：将图（1）中的绕点逆时针旋转，当点落在边上时，交于点，如图（2）．发现：．请证明这个结论．(2)    实践探究：将图（1）中的绕点顺时针旋转（），当，，三点在同一条直线上时，连接，如图（3）．请解答以下问题：①求证：；②探究线段，，之间的数量关系，并说明理由．