4.3 等可能条件下的概率（二）-2023-2024学年九年级数学上册教材配套教学课件（苏科版）

这是一份4.3 等可能条件下的概率（二）-2023-2024学年九年级数学上册教材配套教学课件（苏科版），共19页。

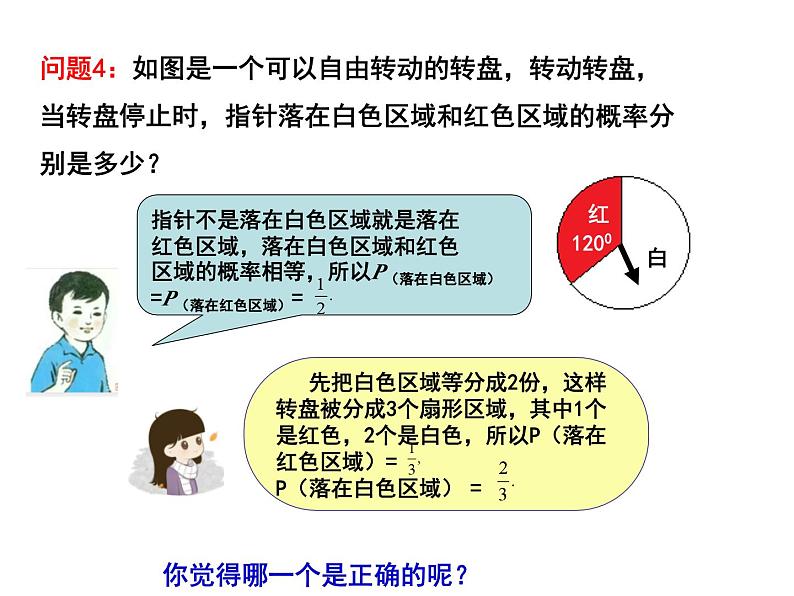
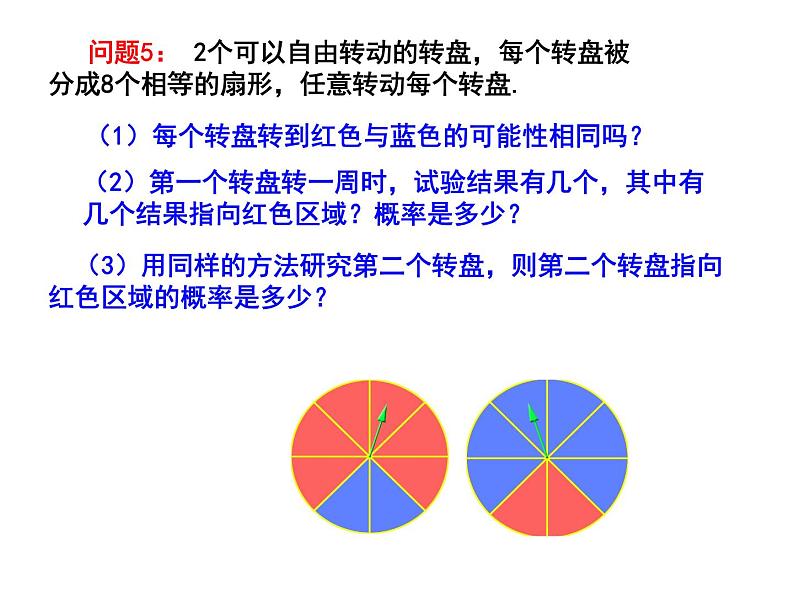
4.3 等可能条件下的概率（二） 小颖为学校联欢会设计一个“配紫色”游戏：如下图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形.小明同时转动两个转盘，如果转盘A转出红色，转盘B转出了蓝色，那么他就赢了，因为红色和蓝色在一起配成了紫色.A盘B盘情境引入问题：你能求出小明获胜的概率吗？ 问题1：出示一个带指针的转盘，任意转动这个转盘，如果在某个时刻观察指针的位置 . （1）这时所有可能结果有多少个？（2）每次观察有几个结果？有无第二个结果？ （3）每个结果出现的机会是均等的吗？新课讲解（2）怎样求指针指向每一个扇形区域的概率呢？（1）当转盘停止时，指针指向每一个扇形区域的机会均等吗？ 问题2：现将转盘被分成8个面积相等的扇形，并标上1、2、3……8，若每个扇形面积为单位1，转动转盘，转盘的指针的位置在不断地改变.问题3：现将转盘涂色，颜色为红、蓝、白三种颜色．（1）转动转盘的试验所有等可能出现的结果数？（2）事件指针指向红色区域可能发生的结果数？（3）怎样计算指针指向红色区域的概率？（4）你能计算出指针指向白色区域的概率吗？问题4：如图是一个可以自由转动的转盘，转动转盘，当转盘停止时，指针落在白色区域和红色区域的概率分别是多少？指针不是落在白色区域就是落在红色区域，落在白色区域和红色区域的概率相等，所以P（落在白色区域）=P（落在红色区域）=你觉得哪一个是正确的呢？ （1）每个转盘转到红色与蓝色的可能性相同吗？ 问题5： 2个可以自由转动的转盘，每个转盘被分成8个相等的扇形，任意转动每个转盘. （2）第一个转盘转一周时，试验结果有几个，其中有几个结果指向红色区域？概率是多少？ （3）用同样的方法研究第二个转盘，则第二个转盘指向红色区域的概率是多少？ （5）根据上面求概率的方法若要改变这两个转盘指针指向红色区域的概率，需要改变什么？（4）哪一个转盘指向红色区域概率大？你认为概率大小与什么因素有直接关系？ 小颖为学校联欢会设计一个“配紫色”游戏：如下图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形.小明同时转动两个转盘，如果转盘A转出红色，转盘B转出了蓝色，那么他就赢了，因为红色和蓝色在一起配成了紫色.求小明获胜的概率．A盘B盘回归情境如何利用画树状图或列表的方法表示游戏可能出现的结果？.树状图画树状图如图所示：列表法小明获胜的概率是　例1：某商场制作了一个可以自由转动的转盘（如图），转盘分为24个相同的扇形，其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个．商场规定：顾客每购满1000元的商品，可获得一次转动转盘的机会．当转盘停止转动时，指针指向红、蓝、黄区域，顾客可分别获得500元、100元、50元的礼品．某顾客购物1400元，他获得礼品的概率是多少？获得500元、100元、50元礼品的概率各是多少？例题精讲例2　　在4m 远外向地毯扔沙包，地毯中每一块小正方形除颜色外完全相同，假定沙包击中每一块小正方形是等可能的，扔沙包１次，击中红色区域的概率多大？解：地毯由64块小正方形构成，其中红色小正方形有20块，这些正方形除颜色外都相同.因为扔沙包1次，击中每一块小正方形的可能性都相同，所以P（击中红色区域）= =1.一儿童行走在如图所示的地板上，当他随意停下时， 最终停在地板上阴影部分的概率是(　　)A课堂练习DC4.一只蚂蚁在如图所示的方格地板上随机爬行，每个小方格形状大小完全相同，当蚂蚁停下时，停在地板中阴影部分的概率为_______.5.如果小明将飞镖任意投中如图所示的正方形木板，那么飞镖落在阴影部分的概率是多少？ 小明与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．（1）不考虑其他因素，你认为这个游戏公平吗？说明理由．（2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．拓展延伸1.等可能条件下的几何概型（转盘、方格）的概率 .2.把等可能条件下,实验结果无限个的几何概型通过等积分割转化为古典概型. 课堂小结谈谈这一节课你有哪些收获？