2022-2023学年河南省驻马店市汝南县七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年河南省驻马店市汝南县七年级（下）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题，六小组的频数和为等内容，欢迎下载使用。

2022-2023学年河南省驻马店市汝南县七年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列各数是无理数的是(    )
A. 13 B. 0.201 C. π D. 9
2. 以下调查中，适宜全面调查的是(    )
A. 了解全班同学每周体育锻炼的时间 B. 调查某批次汽车的抗撞击能力
C. 调查春节联欢晚会的收视率 D. 鞋厂检测生产的鞋底能承受的弯折次数
3. 如果a>b，那么下列结论一定正确的是(    )
A. a−3b2 C. a+3−3b
4. 如图，能判定AB//EF的条件是(    )
A. ∠ABD=∠FEC
B. ∠ABC=∠FEC
C. ∠DBC=∠FEB
D. ∠DBC=∠FEC
5. 平面直角坐标系内，点A(−2,−3)在(    )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. 若a=37，b= 5，c=2，则a，b，c的大小关系为(    )
A. b 7. 能作为反例说明命题“若a>−2，则a2>4”是假命题的a的值可以为(    )
A. a=3 B. a=0 C. a=−3 D. a=−2
8. 在如图所示的平面直角坐标系内，画在透明胶片上的▱ABCD，点A的坐标是(0,2).现将这张胶片平移，使点A落在点A′(5,−1)处，则此平移可以是(    )
A. 先向右平移5个单位，再向下平移1个单位
B. 先向右平移5个单位，再向下平移3个单位
C. 先向右平移4个单位，再向下平移1个单位
D. 先向右平移4个单位，再向下平移3个单位

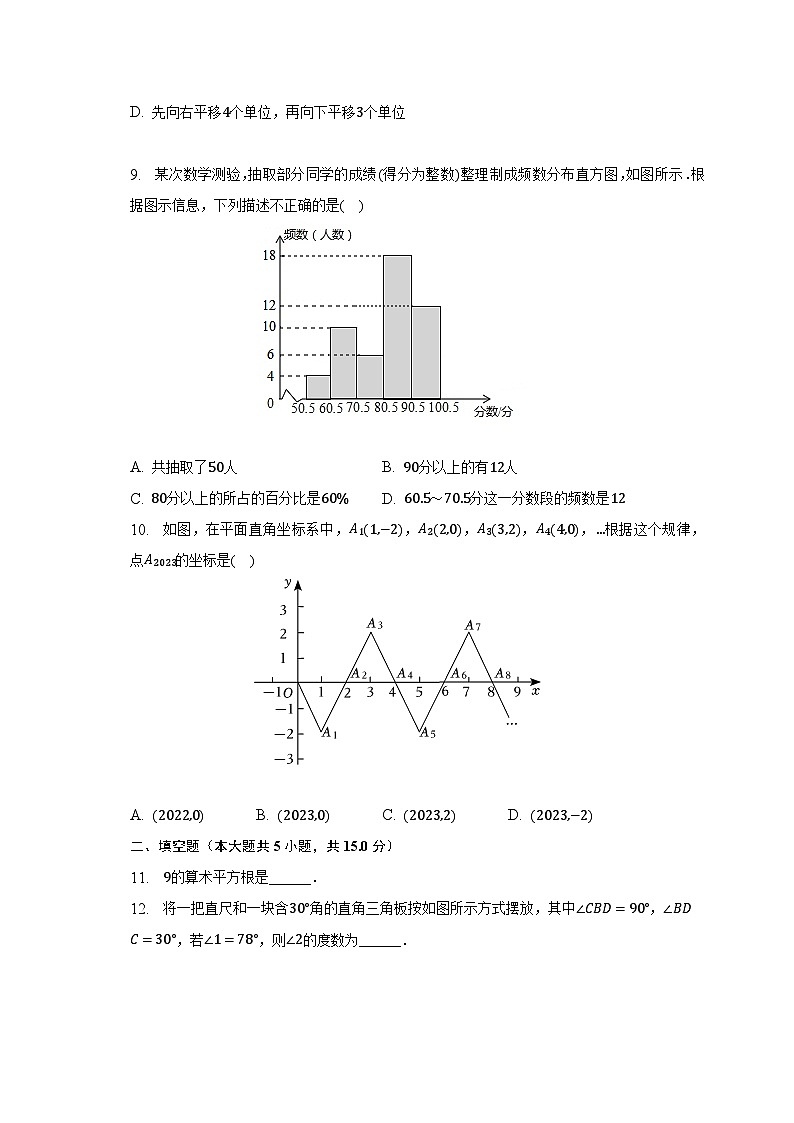
9. 某次数学测验，抽取部分同学的成绩(得分为整数)整理制成频数分布直方图，如图所示．根据图示信息，下列描述不正确的是(    )

A. 共抽取了50人 B. 90分以上的有12人
C. 80分以上的所占的百分比是60% D. 60.5～70.5分这一分数段的频数是12
10. 如图，在平面直角坐标系中，A1(1,−2)，A2(2,0)，A3(3,2)，A4(4,0)，…根据这个规律，点A2023的坐标是(    )

A. (2022,0) B. (2023,0) C. (2023,2) D. (2023,−2)
二、填空题（本大题共5小题，共15.0分）
11. 9的算术平方根是______．
12. 将一把直尺和一块含30°角的直角三角板按如图所示方式摆放，其中∠CBD=90°，∠BDC=30°，若∠1=78°，则∠2的度数为______．

13. 2021年4月28日，某校九年级学生进行了中考体育测试，该校抽取了部分学生的一分钟跳绳测试成绩，并将测试成绩整理后作出如图的直方图.甲同学计算出前两组的总数和为18，乙同学计算出第一组的人数是抽取总人数的4%，丙同学计算出从左至右第二、三、四组的频数比为4：17：15，若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是______ ．

14. 如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面，其中三块横放的墙砖比两块竖放的墙砖低30cm，两块竖放的墙砖比两块横放的墙砖高50cm，则每块墙砖的截面面积是______cm2．


15. 已知点A(3,4)，B(−1,−2)，将线段AB平移到线段CD，点A平移到点C，若平移后点C、D恰好都在坐标轴上，则点C的坐标为______．
三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题8.0分)
(1)计算：3−27+| 3−2|− 94；
(2)已知2a−1的一个平方根是3，3a+6b的立方根是3，求a+b的平方根．
17. (本小题10.0分)
(1)解方程组：3x−y=−4x−2y=−3；
(2)解不等式组：3x+2<4(x+1)x3≥x−32+1，并将其解集表示在如图所示的数轴上．


18. (本小题8.0分)
发现：如图，∠AOB内有一点P：过点P画PC//OB交OA于点C，画PD//OA交OB于点D；根据所画图形试说明：∠O与∠CPD的数量关系；
验证：完善下面的解答过程，并填写理由或数学式：
∵PC//OB
∴∠O=______(______)
∵PD//OA
∴∠CPD=______∴∠O=∠CPD
探究：某数学兴趣小组通过以上练习发现了命题“两边分别平行的两个角相等”，甲同学认为该命题是真命题并画了图1进行验证，乙同学对甲同学的判断提出质疑，认为该命题不一定成立，是假命题，并作图如图2所示，题设与甲同学相同，得到∠B≠∠D，根据乙同学的作图，试判断此时∠B与∠D的数量关系，并说明理由．
归纳：综合甲乙两同学的证明得到结论：两边分别平行的两个角______．



19. (本小题8.0分)
如图，在平面直角坐标系中，三角形ABC的顶点都在网格点上，点A的坐标是(−1,3)．
(1)将三角形ABC先向右平移4个单位长度，再向下平移3个单位长度，得到三角形A′B′C′，画出平移后的三角形A′B′C′，并求出它的面积；
(2)若x轴上有一动点E，当三角形AA′E的面积为12时，请直接写出点E的坐标．

20. (本小题9.0分)
学史明理，学史增信，学史崇德，学史力行，在建党101周年之际，某校对全校学生进行了一次党史知识测试，成绩评定共分为A、B、C、D四个等级，随机抽取了部分学生的成绩进行调查，将获得的数据整理绘制成两幅不完整的统计图.根据统计图提供的信息，解答下列问题：

(1)在这次调查中一共抽取了多少名学生？
(2)B等级的学生有多少人？补全条形统计图；
(3)求D等级所在扇形对应的圆心角度数；
(4)若该校有3000名学生，估计成绩为C等级的有多少人？
21. (本小题10.0分)
“冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物．自2019年正式亮相后，相关特许商品投放市场，持续热销．某冬奥官方特许商品零售店购进了一批同一型号的“冰墩墩”和“雪容融”玩具，连续两个月的销售情况如表：
月份
销售量/件
销售额/元
冰墩墩
雪容融
第1个月
100
40
14800
第2个月
160
60
23380
(1)求此款“冰墩墩”和“雪容融”玩具的零售价格；
(2)某单位欲购买这两款玩具作为冬奥知识竞赛活动的奖品，要求“雪容融”的数量恰好等于“冰墩墩”的数量的2倍，且购买总资金不得超过9000元，请根据要求确定该单位购买“冰墩墩”玩具的最大数量．

22. (本小题10.0分)
定义：把ax+y=b(其中a，b是常数，x，y是未知数)这样的方程称为“优美二元一次方程”.当y=2x时，“优美二元一次方程ax+y=b”中x的值称为“优美二元一次方程”的“优美值”.例如：当y=2x时，“优美二元一次方程”3x−y=4化为3x−2x=4，解得：x=4，故其“优美值”为4．
(1)求“优美二元一次方程”5x−y=1的“优美值”；
(2)若“优美二元一次方程”13x+y=m的“优美值”是−3，求m的值；
(3)是否存在n，使得优美二元一次方程52x+y=n与优美二元一次方程4x−y=n−2的“优美值”相同？若存在，请求出n的值及此时的“优美值”；若不存在，请说明理由．
23. (本小题12.0分)
问题情景：
如图，AB//CD，直线EF与直线CD、直线AB分别交于点P点Q，构成“三线八角”．
探究：(1)在图中，作“三线八角”中任意两个角的角平分线，试判断这两条角平分线的位置关系.请你画出其中四种不同情况的图形，并选择一种进行证明；
发现：(2)把你的发现用一句话概括出来；
拓展：(3)在备用图中，请你在直线EF的右侧平面内任取一点M，连结MP，MQ，探究∠MPD，∠MQB，
∠PMQ之间的关系.请你画出所有不同的情况对应的图形，并直接写出结论．


答案和解析

1.【答案】C 
【解析】解：A、B、D为有理数，不符合题意；
C、π是无限不循环小数，是无理数，符合题意．
故选：C．
根据无理数的概念：无限不循环小数进行选择即可．
本题考查无理数概念，熟记无理数的概念是解题的关键．

2.【答案】A 
【解析】解：A.了解全班同学每周体育锻炼的时间，适合全面调查，故选项A符合题意；
B.调查某批次汽车的抗撞击能力，适合抽样调查，故选项B不符合题意；
C.调查春节联欢晚会的收视率，适合抽样调查，故选项C不符合题意；
D.鞋厂检测生产的鞋底能承受的弯折次数，适合抽样调查，故选项D不符合题意；
故选：A．
根据全面调查得到的调查结果比较准确，但所费人力、物力和时间较多，抽样调查得到的调查结果比较近似进行解答．
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

3.【答案】B 
【解析】解：A.∵a>b，
∴a−3>b−3，故本选项不符合题意；
B.∵a>b，
∴a2>b2，故本选项符合题意；
C.∵a>b，
∴a+3>b+3，故本选项不符合题意；
D.∵a>b，
∴−3a<−3b，故本选项不符合题意，
故选：B．
根据不等式的性质逐个判断即可．
本题考查了不等式的性质，能熟记不等式的性质是解此题的关键，①不等式的性质1：不等式的两边都加(或减)同一个数(或式子)，不等号的方向不变；②不等式的性质2：不等式的两边都乘(或除以)同一个正数，不等号的方向不变；③不等式的性质3：不等式的两边都乘(或除以)同一个负数，不等号的方向改变．

4.【答案】B 
【解析】解：A、当∠ABD=∠FEC，无法判定AB//EF，故选项错误；
B、当∠ABC=∠FEC时，AB//EF，故选项正确；
C、当∠DBC=∠FEB时，无法判定AB//EF，故选项错误；
D、当∠DBC=∠FEC时，BD//EF，故选项错误．
故选：B．
根据平行线的判定定理分别进行判断即可．
本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．

5.【答案】C 
【解析】解：因为点A(−2,−3)的横坐标为负数，纵坐标是负数，
所以点A(−2,−3)在第三象限．
故选：C．
根据各象限内点的坐标特征解答即可．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．

6.【答案】C 
【解析】
【分析】
本题考查实数的大小比较，理解算术平方根、立方根的意义是正确判断的前提．
根据算术平方根、立方根的意义估算出a、b的范围，再进行比较即可．
【解答】
解：∵31<37<38，
∴1<37<2，
即1 又∵2< 5<3，
∴2 ∴a 故选C．  
7.【答案】B 
【解析】解：能作为反例说明命题“若a>−2，则a2>4”是假命题的a的值可以为0，
∵a=0，
∴a2<4，
故此时“若a>−2，则a2>4”是假命题．
故选：B．
根据要证明一个命题结论不成立，可以通过举反例的方法来证明一个命题是假命题．
此题主要考查了利用举例法证明一个命题错误，要说明数学命题的错误，只需举出一个反例即可，这是数学中常用的一种方法．

8.【答案】B 
【解析】解：根据A的坐标是(0,2)，点A′(5,−1)，
横坐标加5，纵坐标减3得出，故先向右平移5个单位，再向下平移3个单位，
故选：B．
利用平面坐标系中点的坐标平移方法，利用点A的坐标是(0,2)，点A′(5,−1)得出横纵坐标的变化规律，即可得出平移特点．
此题主要考查了平面坐标系中点的平移，用到的知识点为：左右移动横坐标，左减，右加，上下移动，纵坐标上加下减．

9.【答案】D 
【解析】解：A.一共调查了4+10+6+18+12=50(人)，因此选项A不符合题意；
B.90分以上的有12人，因此选项B不符合题意；
C.80分以上的所占的百分比为18+1250×100%=60%，因此选项C不符合题意；
D.60.5～70.5分这一分数段的频数为10，不是12，因此选项D符合题意；
故选：D．
根据频数分布直方图中所反映的数据，利用频率=频数总数进行判断即可．
本题考查频数分布直方图，掌握频率=频数总数是正确判断的关键．

10.【答案】C 
【解析】解：观察图形可知，
点的横坐标依次是1、2、3、4、…、n，纵坐标依次是−2、0、2、0、−2、0、2、…，四个一循环，
2023÷4=505……3，
所以点A2023坐标是(2023,2)．
故选：C．
由图形得出点的横坐标依次是1、2、3、4、…、n，纵坐标依次是−2、0、2、0、−2、0、2、…，四个一循环，继而求得答案．
本题考查了规律型：点的坐标，学生的观察图形的能力和理解能力，解题的关键是根据图形得出规律．

11.【答案】3 
【解析】解：因为32=9，
所以9的算术平方根是3．
故答案为：3．
根据算术平方根的定义解答即可．
本题考查了数的算术平方根，解题的关键是牢记算术平方根为非负数．

12.【答案】18° 
【解析】解：∵∠CBD=90°，∠1=78°，
∴∠DBE=180°−∠CBD−∠1=180°−90°−78°=12°，
∵直尺的两边平行，即EA//GH，
∴∠BDF=∠DBE=12°，
∵∠BDC=30°，
∴∠2=∠BDC−∠BDF=30°−12°=18°．
故答案为：18°．
先根据邻补角的定义求出∠DBE的度数，再根据平行线的性质得出∠BDF=∠DBE，最后根据∠BDC=30°求出∠2即可求出答案．
本题主要考查了平行线的性质，能灵活运用平行线的性质定理进行推理是解此题的关键．

13.【答案】24% 
【解析】解：∵前两组的频数和是18，第一组的人数是抽取总人数的4%，
∴抽取的总人数=(18−12)÷4%=150(人)，
∵第二、三、四组的频数比为：4：17：15，第二小组的频数为12，
∴第三、四组的频数分别为：51、45，
∴第五、六小组的频数和为：150−(6+12+51+54)=36(人)，
∴这次测试成绩的优秀率为：36150×100%=24%；
故答案为：24%．
利用频数=总数×频率，可得抽调的总人数，再计算出前四小组的总人数即可求解；
本题主要考查频数分布直方图的能力和利用统计图获取信息的能力，利用统计图获取信息进行求解是解题的关键．

14.【答案】900 
【解析】解：设每块墙砖的长为x cm，宽为y cm，
依题意得：2x−3y=302x−2y=50，
解得：x=45y=20，
∴xy=45×20=900(cm2).
故答案为：900．
设每块墙砖的长为x cm，宽为y cm，根据“三块横放的墙砖比两块竖放的墙砖低30cm，两块竖放的墙砖比两块横放的墙砖高50cm”，即可得出关于x，y的二元一次方程组，解之即可得出x，y的值，再将其代入xy中即可求出结论．
本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．

15.【答案】(0,6)或(4,0) 
【解析】解：∵A(3,4)，B(−1,−2)，将线段AB平移到CD，且C，D在坐标轴上，
∴线段AB向右平移1个单位，再向下平移4个单位或向上平移2个单位，再向左3个单位，
∴C点坐标为：(0,6)或(4,0)．
故答案为：(0,6)或(4,0)．
首先根据题意画出图形，然后再根据题意进行平移即可．
此题主要考查了坐标与图形的变化，关键是画出坐标系，可以直观的得到答案．

16.【答案】解：(1)3−27+| 3−2|− 94
=−3+2− 3−32
=−52− 3；
(2)∵2a−1的一个平方根是3，3a+6b的立方根是3，
∴2a−1=32，3a+6b=27，
解得：a=5，b=2，
∴a+b=7，
∴a+b的平方根为：± 7． 
【解析】(1)先利用立方根，平方根，绝对值对式子进行化简，然后再进行运算即可；
(2)由题意可得：2a−1=32，3a+6b=27，从而可求得a，b的值，再代入运算即可．
本题主要考查考查实数的运算，平方根，立方根，解答的关键是理解清楚题意，特别是第(2)题，比较容易出错．

17.【答案】解：(1)3x−y=−4①x−2y=−3②，
②×3得：3x−6y=−9③，
③−①得：5y=5，
解得：y=1，
把y=1代入①得：3x−1=−4
解得：x=−1，
∴原方程组的解为：x=−1y=1；
(2)3x+2<4(x+1)①x3≥x−32+1②，
解不等式①得：x>−2，
解不等式②得：x≤3，
∴原不等式组的解集为：−2 ∴该不等式组的解集在数轴上表示如图所示：
 
【解析】(1)利用加减消元法进行计算，即可解答；
(2)按照解一元一次不等式组的步骤，进行计算即可解答．
本题考查了解一元一次不等式组，解二元一次方程组，在数轴上表示不等式的解集，准确熟练地进行计算是解题的关键．

18.【答案】ACP  两直线平行，同位角相等  ∠ACP  相等或互补 
【解析】解：验证：如图，

∵PC//OB，
∴∠O=∠ACP(两直线平行，同位角相等)，
∵PD//OA，
∴∠CPD=∠ACP(两直线平行，内错角相等)，
∴∠O=∠CPD．
故答案为：∠ACP；两直线平行，同位角相等；∠ACP；
探究：两边分别平行的两个角相等或互补，理由：
如图1，
∵DF//BC，
∴∠D=∠CGE．
∵DE//BA，
∴∠B=∠CGE，
∴∠D=∠B．
∴两边分别平行的两个角相等；
如图2，
∵DF//BC，
∴∠D=∠DGB．
∵DE//BA，
∴∠B+∠DGB=180°，
∴∠D+∠B=180°．
∴两边分别平行的两个角互补，
综上，两边分别平行的两个角相等或互补．
故答案为：相等或互补．
验证：利用平行线的性质和等量代换进行填空即可；
探究：结合图1和图2，利用平行线的性质解答即可．
本题主要考查了平行线的性质，对顶角相等，分类讨论是思想方法，等量代换，熟练掌握平行线的性质是解题的关键．

19.【答案】解：(1)如图，三角形A′B′C′为所画的三角形．

S△A′B′C′=12×5×4=10；

(2)设E(m,0).则有12×|m−3|×3=12，
解得m=11或−5，
∴E(11,0)或E(−5,0)． 
【解析】(1)利用平移变换的性质分别作出A，B，C的对应点A′，B′，C′即可；
(2)设E(m,0)，构建方程求解即可．
本题考查作图−平移变换，三角形的面积等知识，解题的关键是掌握平移变换的性质，学会用分割法求三角形面积．

20.【答案】解：(1)32÷40%=80(名)，
(2)B等级的学生为80×20%=16(人)
补全条形统计图如下：

(3)D等级所对应的扇形圆心角的度数为：360°×880=36°；
(4)3000×2480=900(人)．
答：估计该校3000学生中有900名学生的成绩评定为C等级． 
【解析】(1)根据A等级的人数以及所占的百分比即可求出本次调查中共抽取的学生数；
(2)根据(1)中的结果和扇形统计图中的数据，可以计算出B等级的人数，然后即可将条形统计图补充完整；
(3)根据D等级的人数以及抽取的学生数计算出D等级所对应的扇形圆心角的度数；
(4)求出C等级所占整体的百分比即可求出相应的人数．
本题考查扇形统计图、条形统计图，理解两个统计图中数量关系是解决问题的关键．

21.【答案】解：(1)设“冰墩墩”和“雪容融”玩具的单价分别为x、y元，
则100x+40y=14800160x+60y=23380，
解方程组得：
x=118y=75，
答：“冰墩墩”和“雪容融”玩具的单价分别为118、75元．
(2)设“冰墩墩”玩具的数量为m个，则“雪容融”玩具为2m个．
则118m+75⋅2m≤9000，
解得：m≤225067≈33.58，
正整数m最大为33，
答：该单位购买“冰墩墩”玩具的最大数量为33． 
【解析】(1)分别设出冰墩墩和雪容融的单价，根据题中的等量关系列出方程组，解方程组，最后作答．
(2)设出冰墩墩玩具为m个，列出不等式，取最大整数解即可．
本题主要考查了二元一次方程组和一元一次不等式的应用，读懂题意，列出对应的方程组或不等式是解题的关键．

22.【答案】解：(1)令y=2x，则“优美二元一次方程”5x−y=1化为：5x−2x=1，x=13，
其“优美值”为13．
(2)令y=2x，则“优美二元一次方程”13x+y=m化为：13x+2x=m，
把x=−3代入，得m=−7．
(3)令y=2x，则“优美二元一次方程”52x+y=n化为：52x+2x=n，x=2n9，
其“优美值”为2n9．
令y=2x，则“优美二元一次方程”4x−y=n−2化为：4x−2x=n−2，x=n−22，
其“优美值”为n−22．
假设“优美值”相同，
∴2n9=n−22，
∴n=185，
∴x=45即“优美值”为45． 
【解析】(1)令y=2x，则“优美二元一次方程”5x−y=1化为：5x−2x=1，解方程即可求解；
(2)令y=2x，则“优美二元一次方程”13x+y=m化为：13x+2x=m，将把x=−3代入，即可求解；
(3)令y=2x，则“优美二元一次方程”52x+y=n化为：52x+2x=n，令y=2x，则“优美二元一次方程”4x−y=n−2化为：4x−2x=n−2，根据“优美值”相同，列出关于n的一元一次方程，解方程即可求解．
本题考查二元一次方程的解，理解新定义，熟练掌握一元一次方程的解法是解题的关键．

23.【答案】解：(1)


证明
(第3个图形)
已知：AB//CD，PG，QH分别平分∠CPF，∠EQB，求证：PG//QH．
证明：∵PG，QH分别平分∠CPF，∠EQB，
∴∠QPF=12∠CPF，∠PQH=12∠PQB，
∵AB//CD，
∴∠CPF=∠PQB，
∴∠QPF=∠PQH，
∴PG//QH；
(第1个图形)
已知：AB//CD，PG，PH分别平分∠CPQ，∠EPD，求证：P，Q，H三点共线．
证明：∵PG，PH分别平分∠CPQ，∠EPD，
∴∠QPF=12∠CPF，∠EPH=12∠EPD，
∵∠CPF=∠EPD，
∴∠QPF=∠EPH，
∴∠EPH+∠EPG=∠QPG+∠EPG=180°，
∴P，Q，H三点共线．
(第2个图形)
已知：AB//CD，GQ，QH分别平分∠AQP，∠EQB，求证：QG⊥QH．
证明：∵QG，PH分别平分∠AQP，∠EQB，
∴∠GQP=12∠AQP，∠EQH=12∠EQB，
∵∠AQP+∠EQB=180°，
∴∠GQP+∠EQH=90°，
即：∠GQH=90°，
∴QG⊥QH．
(第4个图形)
已知：AB//CD，PN，QM分别平分∠CPQ，∠AQP，求证：QM⊥PN．
证明：∵PN，QM分别平分∠CPQ，∠AQP，
∴∠NPF=12∠CPF，∠MQE=12∠PQA，
∵AB//CD，
∴∠CPF+∠AQE=180°，
∴∠NPF+∠MQE=90°
∴∠PIQ=90°，
∴QM⊥PN.；

(2)对顶角的角平分线在一条直线上；
邻补角的角平分线互相垂直；
两平行线构成的同位角的角平分线平行；
两平行线构成的内错角的角平分线平行；
两平行线构成的同旁内角的角平分线垂直；
(3)


对顶角的角平分线在一条直线上；
邻补角的角平分线互相垂直；
两平行线构成的同位角的角平分线平行；
两平行线构成的内错角的角平分线平行；
两平行线构成的同旁内角的角平分线垂直； 
【解析】(1)利用平行线的性质及判定求解；
(2)语言通顺即可；
(3)利用平行线的性质求解．
本题考查了平行线性质和判定，分类讨论是解题的关键．