2022-2023学年湖北省十堰市郧阳区七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年湖北省十堰市郧阳区七年级（下）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

2022-2023学年湖北省十堰市郧阳区七年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 在平面直角坐标系中，点A(−2,−3)位于(    )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 4的算术平方根是(    )
A. ±2 B. −2 C. 2 D. 2
3. 下列调查中，适宜抽样调查的是(    )
A. 了解七(1)班学生校服的尺码情况 B. 了解某班学生对“创文知识”的知晓率
C. 对“神舟十六号”零部件的检查 D. 调查某批次汽车的抗撞击能力
4. 如图，直线a/​/b，三角板的直角顶点放在直线b上，两直角边与直线a相交，如果∠2=27°，那么∠1等于(    )


A. 53° B. 63° C. 27° D. 37°
5. 某个关于x的一元一次不等式组的解集在数轴上表示如图，则该解集是(    )

A. −2 6. 已知x=−2y=a是方程2x+3y=5的解，则a的值为(    )
A. 3 B. −3 C. 13 D. −13
7. 已知方程组3x+y=k+1x+3y=3的解满足x+y<1，则k的取值范围是(    )
A. k<−3 B. k>−3 C. k<0 D. k>0
8. 我国古代数学名著《算法统宗》中记载：“今有绫七尺，罗九尺，共价适等；只云罗每尺价比绫每尺少钱三十六文，问各钱价若干？”意思是：现在有一匹7尺长的绫布和一匹9尺长的罗布恰好一样贵，只知道每尺罗布比绫布便宜36文，问两种布每尺各多少钱？设绫布每尺x文，罗布每尺y文，那么可列方程组为(    )
A. x7=y9x−y=36 B. x7=y9y−x=36 C. 7x=9yx−y=36 D. 7x=9yy−x=36
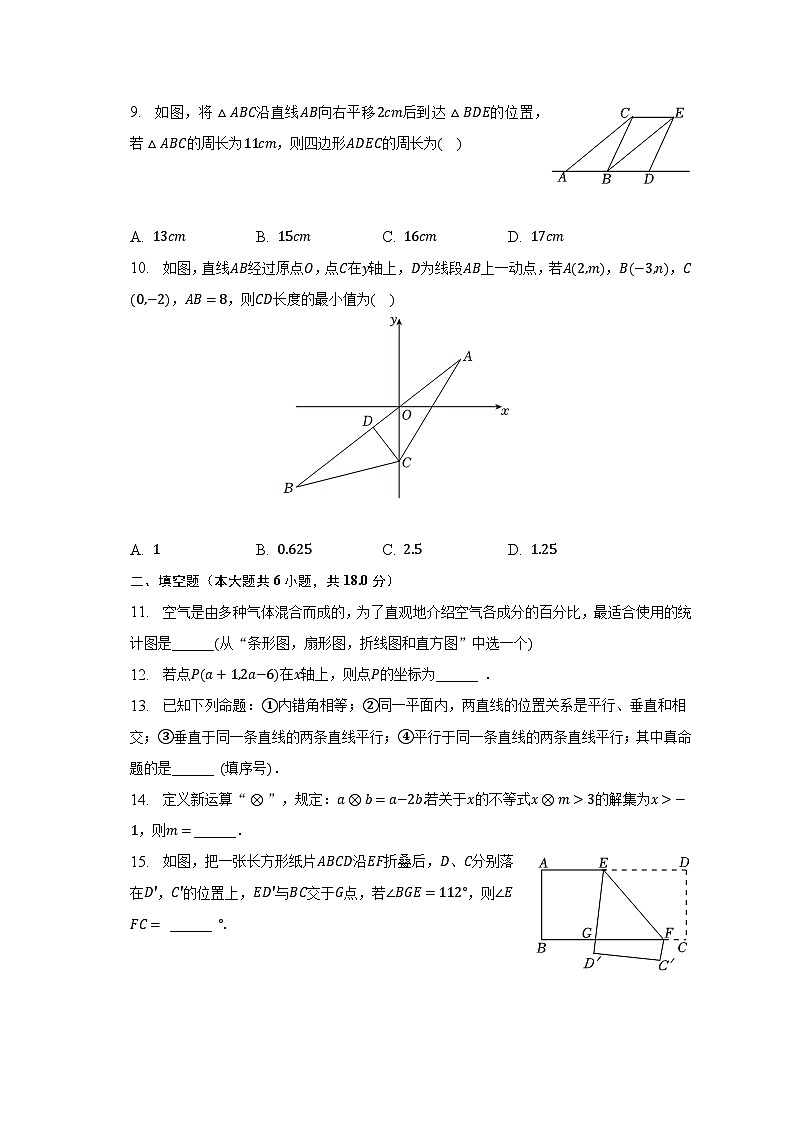
9. 如图，将△ABC沿直线AB向右平移2cm后到达△BDE的位置，若△ABC的周长为11cm，则四边形ADEC的周长为(    )


A. 13cm B. 15cm C. 16cm D. 17cm
10. 如图，直线AB经过原点O，点C在y轴上，D为线段AB上一动点，若A(2,m)，B(−3,n)，C(0,−2)，AB=8，则CD长度的最小值为(    )

A. 1 B. 0.625 C. 2.5 D. 1.25
二、填空题（本大题共6小题，共18.0分）
11. 空气是由多种气体混合而成的，为了直观地介绍空气各成分的百分比，最适合使用的统计图是______(从“条形图，扇形图，折线图和直方图”中选一个)
12. 若点P(a+1,2a−6)在x轴上，则点P的坐标为______ ．
13. 已知下列命题：①内错角相等；②同一平面内，两直线的位置关系是平行、垂直和相交；③垂直于同一条直线的两条直线平行；④平行于同一条直线的两条直线平行；其中真命题的是______ (填序号)．
14. 定义新运算“⊗”，规定：a⊗b=a−2b.若关于x的不等式x⊗m>3的解集为x>−1，则m=______．
15. 如图，把一张长方形纸片ABCD沿EF折叠后，D、C分别落在D′，C′的位置上，ED′与BC交于G点，若∠BGE=112°，则∠EFC= ______ °.


16. 如图，在平面直角坐标系xOy中，动点P按图中箭头所示方向依次运动，第1次从点(−1,0)运动到点(0,1)，第2次运动到点(1,0)，第3次运动到点(2,−2)，…按这样的运动规律，动点P第2023次运动后的点坐标为______ ．


三、计算题（本大题共2小题，共13.0分）
17. 解方程组：
(1)y=2x−33x+2y=8；
(2)5x+2y=253x+4y=15．
18. 解不等式组3(x−1)<5x+14x−13≥2x−1，并把解集在数轴上表示出来．
四、解答题（本大题共7小题，共59.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题6.0分)
计算下列各式的值：
(1) 16−3−1+|2− 3|．
(2) 7( 7+1 7)−38．
20. (本小题7.0分)
如图所示，点E在直线CD上，∠BAE+∠AED=180°，在AB、CD之间的点M、N分别在线段AE的两侧(点M在点N右侧)，且∠M=∠N，标记∠BAM为∠1，∠NEC为∠2，求证：∠1=∠2．
证明：∵∠M=∠N(已知)，
∴______(______).
∴∠MAE=______(______).
∵______(已知)，
∴AB/​/CD(______).
∴______=∠AEC(两直线平行，内错角相等)．
∴______=∠2+∠AEN．
∴∠1=∠2(等式的性质)．

21. (本小题8.0分)
目前“微信”“支付宝”“共享单车”和“网购”给我们的生活带来了很多便利，某校七年级数学小组在校内对“你最认可的新生事物”进行调查，随机调查了m名学生(每名学生必选一种且只能从这四种中选择一种)，并将调查结果绘制成如图所示不完整的统计图．
(1)根据图中信息，求出m= ______ ，n= ______ ；
(2)请把条形统计图补充完整；
(3)根据抽样调查的结果，请估算在全校2000名学生中，最认可“微信”和“支付宝”这两样新生事物的学生共有多少名？


22. (本小题8.0分)
平面直角坐标系内，已知A(2,1)，B(4,2)，C(−1,4)，平移线段BC得到对应线段AD(点B与点A对应)．
(1)画出平移后的线段AD，并写出D点坐标；
(2)求四边形ABCD的面积；
(3)若线段AD交y轴于点P，请直接写出点P的坐标．

23. (本小题8.0分)
如图，已知∠1=∠BDC，∠2+∠3=180°，
(1)问AD与EC平行吗？试说明理由；
(2)若DA平分∠BDC，CE⊥AE于E，∠1=70°，试求∠FAB的度数．

24. (本小题10.0分)
茶叶是郧阳区的支柱产业之一，某茶叶店准备从茶农处采购甲、乙两种不同品质的茶叶，已知采购2斤甲型茶叶和1斤乙型茶叶共需要550元，采购3斤甲型茶叶和2斤乙型茶叶共需要900元．
(1)采购甲、乙两种型号的茶叶每斤分别多少元？
(2)该茶叶店准备用不超过3500元的资金采购甲、乙两种型号的茶叶共20斤，其中购进甲种型号的茶叶的斤数不少于购进乙种茶叶的23，采购的斤数需为整数，那么该茶店有哪几种采购方案？
(3)在(2)的条件下，已知该茶叶店销售甲型茶叶1斤可获利3m(m>0)元，销售乙型茶叶1斤可获利4m元，若20斤茶叶全部售出的最大利润为936元，请直接写出m的值______ ．
25. (本小题12.0分)
在平面直角坐标系中，A(a,0)，C(0,c)，且a，c满足 a−2+(c−3)2=0．
(1)直接写出a，c的值．
(2)如图1，点B(4,4)，在第二象限内有一点P(m,12)，若S四边形ACPO>12S△ABC，求m的取值范围．
(3)如图2，若∠DOA=∠DAO，点G是第二象限内一点，并且y轴平分∠GOD.点E是线段OC上一动点，连接AE交OD于点H，当点E在OC上运动时，∠OHA−∠CAE∠OEA−∠OCA的值是否发生变化？若变化，请说明理由；若不变，请求出其值．


答案和解析

1.【答案】C 
【解析】解：由−2<0，−3<0得点A(−2,−3)在第三象限．
故选：C．
根据各象限内点的坐标特征解答．第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．

2.【答案】C 
【解析】解：4的算术平方根是： 4=2，
故选：C．
根据算术平方根的概念：一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根，记为 a，求出4的算术平方根即可．
本题考查了算术平方根的性质和应用，熟练掌握算术平方根的含义是解题的关键．

3.【答案】D 
【解析】解：A、了解七(1)班学生校服的尺码情况，适合普查，故本选项不符合题意；
B、了解某班学生对“创文知识”的知晓率，适合普查，故本选项不符合题意；
C、对“神舟十六号”零部件的检查，适合普查，故本选项不符合题意；
D、调查某批次汽车的抗撞击能力，适宜采用抽样调查，故本选项符合题意．
故选：D．
由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
本题考查了抽样调查和全面调查，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

4.【答案】B 
【解析】解：如图所示：

∵a/​/b
∴∠1=∠3，且∠4=90°，
∴∠2+∠3=90°，
∴∠3=90°−∠2=63°，
∴∠1=63°，
故选：B．
由平行可得∠1=∠3，又结合直角定义可得出∠3+∠2=90°，可求得答案．
本题主要考查平行线的性质，掌握平行线的判定和性质是解题的关键，即①同位角相等⇔两直线平行，②内错角相等⇔两直线平行，③同旁内角互补⇔两直线平行．

5.【答案】B 
【解析】解：表示的解集是：−2 故选B．
根据数轴可知解集表示−2和3之间(包括3)的点表示的部分，据此即可求解．
本题考查了用数轴表示不等式的解集时，要注意“两定”：一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点；二是定方向，定方向的原则是：“小于向左，大于向右”．

6.【答案】A 
【解析】解：把x=−2y=a代入方程2x+3y=5，得：
−4+3a=5，
解得a=3．
故选：A．
把x=−2y=a代入方程计算即可求出a的值．
此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．

7.【答案】C 
【解析】解：3x+y=k+1①x+3y②，
①+②，得
4x+4y=k+4，
∴x+y=k+44，
∵x+y<1，
∴k+44<1，
解得
k<0．
故选：C．
用①+②求出x+y=k+44，然后根据x+y<1列不等式求解即可．
本题考查了二元一次方程组的解法，一元一次不等式的解法，求出x+y=k+44是解答本题的关键．

8.【答案】C 
【解析】解：∵一匹7尺长的绫布和一匹9尺长的罗布恰好一样贵，
∴7x=9y；
∵每尺罗布比绫布便宜36文，
∴x−y=36．
∴根据题意可列出方程组7x=9yx−y=36．
故选：C．
根据“一匹7尺长的绫布和一匹9尺长的罗布恰好一样贵，且每尺罗布比绫布便宜36文”，即可得出关于x，y的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组以及数学常识，找准等量关系，正确列出二元一次方程组是解题的关键．

9.【答案】B 
【解析】解：由平移的性质可知，AB=BD=CE=2cm，
∵△ABC的周长为11cm，即AB+BC+AC=11cm，
∴四边形ADEC的周长为AC+AB+BD+DE+CE=11+2+2=15(cm)，
故选：B．
根据平移的性质得到AB=BD=CE=2cm，再根据周长的定义进行计算即可．
本题考查平移的性质，理解平移的定义，掌握平移的性质是正确解答的关键．

10.【答案】D 
【解析】解：如图：分别过点A、B作y轴的垂线，垂足分别为点E、点F，设△ABC的边AB上的高为x，

∵A(2,m)，B(−3,n)，C(0,−2)．
∴AE=2，BF=3，OC=2；
设三角形ABC中AB边上的高为x，
由S△ABC=S△AOC+S△BOC，
得12×AB×x=12×2×2+12×2×3，
解得：AB×x=10，
∵AB=8，
∴x=1.25
当CD⊥AB时，CD有最小值为x，
∴CD长度的最小值为1.25，
故选：D．
分别过点A、B作y轴的垂线，垂足分别为点D点F，得出AE=2，BF=3，OC=2最后利用三角形的面积解决问题．
本题考查了坐标与图形性质及三角形的面积，掌握：三角形的面积等于底边长与高线乘积的一半，即S=12×底×高是解题的关键．

11.【答案】扇形图 
【解析】解：根据题意，得：直观地介绍空气各成分的百分比，最适合使用的统计图是扇形统计图．
故答案为：扇形统计图．
扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；
折线统计图表示的是事物的变化情况；
条形统计图能清楚地表示出每个项目的具体数目；
频数分布直方图，清楚显示在各个不同区间内取值，各组频数分布情况，易于显示各组之间频数的差别．
此题考查扇形统计图、折线统计图、条形统计图各自的特点．

12.【答案】(4,0) 
【解析】解：∵点P(a+1,2a−6)在x轴上，
∴2a−6=0，
解得a=3，
∴a+1=4
则点P的坐标为(4,0)．
故答案为：(4,0)．
根据x轴上点的坐标的特点y=0，计算出a的值，从而得出点P坐标．
本题主要考查了点的坐标，解题的关键是掌握在x轴上的点的坐标的特点y=0．

13.【答案】④ 
【解析】解：①两直线平行，内错角相等；故①错误，假命题；
②同一平面内，两直线的位置关系是平行和相交，垂直是相交的一种特殊情况，故②错误，假命题；
③在同一平面内，垂直于同一条直线的两条直线平行，故③错误，假命题；
④平行于同一条直线的两条直线平行，故④正确，真命题；
故答案为：④．
根据平行线的性质、平行公理及推论进行判断即可．
考查了命题与定理的知识，解题的关键是了解平线的性质、平行公理及推论，难度较小．

14.【答案】−2 
【解析】解∵a⨂b=a−2b，
∴x⨂m=x−2m．
∵x⨂m>3，
∴x−2m>3，
∴x>2m+3．
∵关于x的不等式x⨂m>3的解集为x>−1，
∴2m+3=−1，
∴m=−2．
故答案为：−2．
根据定义新运算的法则得出不等式，解不等式；根据解集列方程即可．
本题考查了新定义计算在不等式中的运用，读懂新定义并熟练的解不等式是解题的关键．

15.【答案】124 
【解析】解：∵四边形ABCD是长方形，
∴AD/​/BC，
∴∠BGE=∠DEG，
∵∠BGE=112°，
∴∠DEG=112°，
由折叠的性质得∠DEF=∠D′EF，
∴∠DEF=56°，
∵AD/​/BC，
∴∠DEF+∠EFC=180°，
∴∠EFC=180°−56°=124°，
故答案为：124．
先根据矩形的性质得出AD//BC，再根据平行线的性质得出∠BGE=∠DEG=112°，再根据折叠的性质得出∠DEF=∠D′EF，于是得出∠DEF的度数，最后根据两直线平行，同旁内角互补即可求出∠EFC的度数．
本题考查了矩形的性质、平行线的性质和折叠的性质，熟练掌握平行线的性质和折叠的性质是解题的关键．

16.【答案】(2022,−2) 
【解析】解：点P的运动规律是每运动四次向右平移四个单位，
∵2023=505×4……3，
∴动点P第2022次运动时向右505×4+3=2023个单位，
∴点P此时坐标为(2022,−2)，
故答案为：(2022,−2)．
观察图形可知，每4次运动为一个循环组循环，并且每一个循环组向右运动4个单位，用2023除以4，然后根据商和余数的情况确定运动后点的坐标即可．
本题为平面直角坐标系下的规律探究题，解答时注意探究动点的运动规律，又要注意动点的坐标的所在象限及符号．

17.【答案】解：(1)y=2x−3①3x+2y=8②，
把①代入②，得：3x+2(2x−3)=8，
解得：x=2，
把x=2代入①，得：y=1，
∴方程组的解为x=2y=1；
(2)5x+2y=25①3x+4y=15②，
①×2，得：10x+4y=50③，
③−②，得：7x=35，
解得：x=5，
把x=5代入①，得：25+2y=25，
解得：y=0，
∴方程组的解为x=5y=0． 
【解析】本题查看消元法解二元一次方程组，掌握解方程组的步骤是解题关键．
(1)用代入消元法解二元一次方程组；
(2)用加减消元法解二元一次方程组．

18.【答案】解：由3(x−1)<5x+1得，x>−2，
由4x−13≥2x−1得，x≤1，
故不等式组的解集为−2 在数轴上表示为：． 
【解析】分别解两个不等式，然后求解集公共部分即可．
本题考查解一元一次不等式组，解题关键是准确求解各个不等式的解集，最后确定解集公共部分．

19.【答案】解：(1) 16−3−1+|2− 3|
=4−(−1)+(2− 3)
=4+1+2− 3
=7− 3；
(2) 7( 7+1 7)−38
=7+1−2
=6． 
【解析】(1)根据算术平方根、立方根、绝对值的定义计算；
(2)根据二次根式的计算法则，立方根的定义计算即可．
本题考查了实数的运算，解题的关键是熟练掌握算术平方根、立方根、绝对值的定义，二次根式的混合运算．

20.【答案】AM//NE  内错角相等，两直线平行  ∠NEA  两直线平行，内错角相等  ∠BAE+∠AED=180°  同旁内角互补，两直线平行  ∠BAE  ∠1+∠MAE 
【解析】证明：∵∠M=∠N(已知)，
∴AM//NE(内错角相等，两直线平行)，
∴∠MAE=∠AEN(两直线平行，内错角相等)，
∵∠BAE+∠AED=180°，(已知)，
∴AB/​/CD(同旁内角互补，两直线平行)，
∴∠BAE=∠AEC(两直线平行，内错角相等)，
∴∠1+∠MAE=∠2+∠AEN，
∴∠1=∠2(等式的性质)．
故答案为：AM//NE；内错角相等，两直线平行；∠NEA；两直线平行，内错角相等；∠BAE+∠AED=180°；∠BAE；∠1+∠MAE．
根据平行线的判定定理与性质定理及角的和差求解即可．
此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．

21.【答案】100  35 
【解析】解：(1)10÷10%=100(人)，即m=100，
“网购”人数：100×15%=15(人)，
“支付宝”人数：100−40−15−10=35(人)，35÷100=35%，因此n=35，
故答案为：100，35；
(2)补全条形统计图如图所示：

(3)2000×40+35100=1500(人)，
答：全校1800名学生中，最认可“微信”和“支付宝”这两样新生事物的大约有1500人．
(1)样本中，认可“共享单车”的有10人，占被调查人数的10%，可求出被调查人数，即m的值，进而求出“网购”的人数，“支付宝”的人数和所占的百分比，确定n的值；
(2)求出“支付宝”“网购”人数即可补全条形统计图；
(3)样本中，“微信”和“支付宝”占被调查人数的40+35100，因此估计总体1800人中“微信”和“支付宝”也占40+35100．
本题考查条形统计图、扇形统计图的意义和制作方法，掌握两个统计图中数量关系是正确解答的前提．

22.【答案】解：(1)如图，线段AD即为所求；
(2)四边形ABCD的面积=3×7−2×12×1×2−2×12×2×5=9；
(3)设直线AD的解析式为y=kx+b，
∵A(2,1)，D(−3,3)，
则有2k+b=1−3k+b=3，解得k=−25b=95，
∴直线AD的解析式为y=−25x+95，
∴P(0,95).
 
【解析】(1)利用平移变换的性质作出点C的对应点D即可；
(2)利用割补法求出四边形面积即可；
(3)求出直线AD的解析式，可得结论．
本题考查作图−平移变换，四边形的面积，一次函数的性质等知识，解题的关键是掌握平移变换的性质，学会根据一次函数，确定点的坐标，属于中考常考题型．

23.【答案】解：(1)AD//EC.理由如下：
∵∠1=∠BDC，
∴AB/​/CD，
∴∠2=∠ADC，
又∵∠2+∠3=180°，
∴∠ADC+∠3=180°，
∴AD/​/EC；
(2)∵DA平分∠BDC
∴∠ADC=12∠BDC=12∠1=12×70°=35°，
∴∠2=∠ADC=35°，
又∵CE⊥AE，AD/​/EC，
∴∠FAD=∠AEC=90°，
∴∠FAB=∠FAD−∠2=90°−35°=55°． 
【解析】(1)直接利用平行线的判定与性质得出AB/​/CD，进而得出∠ADC+∠3=180°，即可得出答案；
(2)利用角平分线的定义结合已知得出∠FAD=∠AEC=90°，即可得出答案．
此题主要考查了平行线的判定与性质，正确得出∠FAD=∠AEC=90°是解题关键．

24.【答案】11 
【解析】解：(1)设甲型茶叶每斤是x元，乙型茶叶每斤是y元，根据题意得：
2x+y=5503x+2y=900，
解得x=200y=150．
答：甲型茶叶每斤是200元，乙型茶叶每斤是150元；
(2)设购买乙型茶叶a斤，则购买甲型茶叶(20−a)斤，根据题意得：
200(20−a)+150a≤350020−a≥23a，
解得10≤a≤12，
∵a为整数，
∴a=10，11，12，
故该茶店有3种采购方案，
方案一：购买甲型茶叶10斤，乙型茶叶10斤；
方案二：购买甲型茶叶9斤，乙型茶叶11斤；
方案三：购买甲型茶叶8斤，乙型茶叶12斤．
(3)设茶叶全部售出的利润为w元，根据题意得：
w=3m(20−a)+4ma=ma+60m，
∵m>0，
∴w随a的增大而增大，
∴a=12时w有最大值，
即12m+60m=792，
解得m=11．
故答案为：11．
(1)根据题意可以列出相应的方程组，从而可以解答本题；
(2)根据题意可以得到相应的不等式组，从而可以求得有几种采购方案；
(3)根据题意列出函数解析式，再根据总利润的最大值792列出方程，求出m的值．
本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组；(2)根据各数量之间的关系，正确列出一元一次不等式；(3)根据各数量之间的关系，找出w关于m的函数关系式．

25.【答案】解：(1)∵ a−2+(c−3)2=0，
∴a−2=0，c−3=0，
∴a=2，c=3；
(2)∵a=2，c=3，
∴OA=2，OC=3，
∵点P(m,12)在第二象限内，
∴点P到y轴的距离为−m，
过B作BE⊥x轴于E，

则OE=4，BE=4，
∴AE=OE−OA=2，
∵S四边形ACPO=12(OC+BE)⋅OE=12×(3+4)×4=14，S△AOC=12AO⋅OC=12×2×3=3，S△ABE=12AE⋅BE=12×2×4=4，
∴S△ABC=S四边形OCBE−S△AOC−S△ABE=14−3−4=7，
∵S四边形ACPO=S△POC+S△AOC=32×(−m)+3，
∵S四边形ACPO>12S△ABC，
∴32×(−m)+3>12×7，
∴m<−13；
(3)变化，
理由：∵∠AOC=∠DOC+∠ADO=90°，
∴∠OAC+∠ACO=90°，
∵∠DOA=∠DAO，
∴∠OCA=∠DAO，
∵y轴平分∠GOD，
∴∠GOC=∠COD，
∴∠GOC=∠OCA，
∴OG/​/AC，
设∠CAE=α，∠GOC=β，
∴∠GOC=∠OCA=∠COD=β，
如图．过H作HF/​/OG交x轴于F，
∴HF/​/AC，
∴∠FHA=∠CAE=α，
∵OG/​/FH，
∴∠GOD=∠FHO=2β，
∴∠GOD+∠CAE=∠FHO+∠FHA，
∴GOD+∠CAE=∠OHA，
∴∠OHA+∠CAE=∠GOD=2β，
过E作OG的平行线，

同理，∠GOC+∠CAE=∠ORA，
∴∠OEA=∠CAE+∠GOC=α+β，
∵∠OCA=∠GOC=β，
∴∠OEA−∠OCA=α，
∴∠OHA−∠CAE∠OEA−∠OCA=2βαM
∵点E是线段OC上一动点，
∴α的大小在变化，
∵β是个定值，
∴∠OHA−∠CAE∠OEA−∠OCA的值在变化． 
【解析】(1)根据非负数的性质即可得到结论；
(2)根据点P(m,12)在第二象限内，求得点P到y轴的距离为−m，过B作BE⊥x轴于E，则OE=4，BE=4，得到AE=OE−OA=2，根据四边形和扇形的面积公式即可得到结论；
(3)根据余角的性质得到∠OCA=∠DAO，根据角平分线的定义得到∠GOC=∠COD，根据平行线的判定定理得到OG/​/AC，设∠CAE=α，∠GOC=β，得到∠GOC=∠OCA=∠COD=β，过H作HF/​/OG交x轴于F，根据平行线的性质得到∠FHA=∠CAE=α，求得∠GOD=∠FHO=2β，过E作OG的平行线，于是得到结论．
本题是四边形的综合题，考查了非负数的性质，平面内点的坐标特征，平行线的性质，角平分线的定义，四边形和三角形的面积的计算，正确地直线辅助线是解题的关键．