2022-2023学年辽宁省鞍山市七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年辽宁省鞍山市七年级（下）期末数学试卷（含解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年辽宁省鞍山市七年级（下）期末数学试卷
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 如图，点A的坐标是(    )
A. (2,1)
B. (1,2)
C. (2,2)
D. (1,1)
2. 如图，对顶角量角器测得零件的度数是(    )

A. 30° B. 60° C. 150° D. 180°
3. 如图，七年一班学生参加社团活动，其中文学，科技，艺术三个社团的人数比为2：7：3，若参加文学社团的学生有6人，则参加艺术社团的人数是(    )
A. 6人
B. 7人
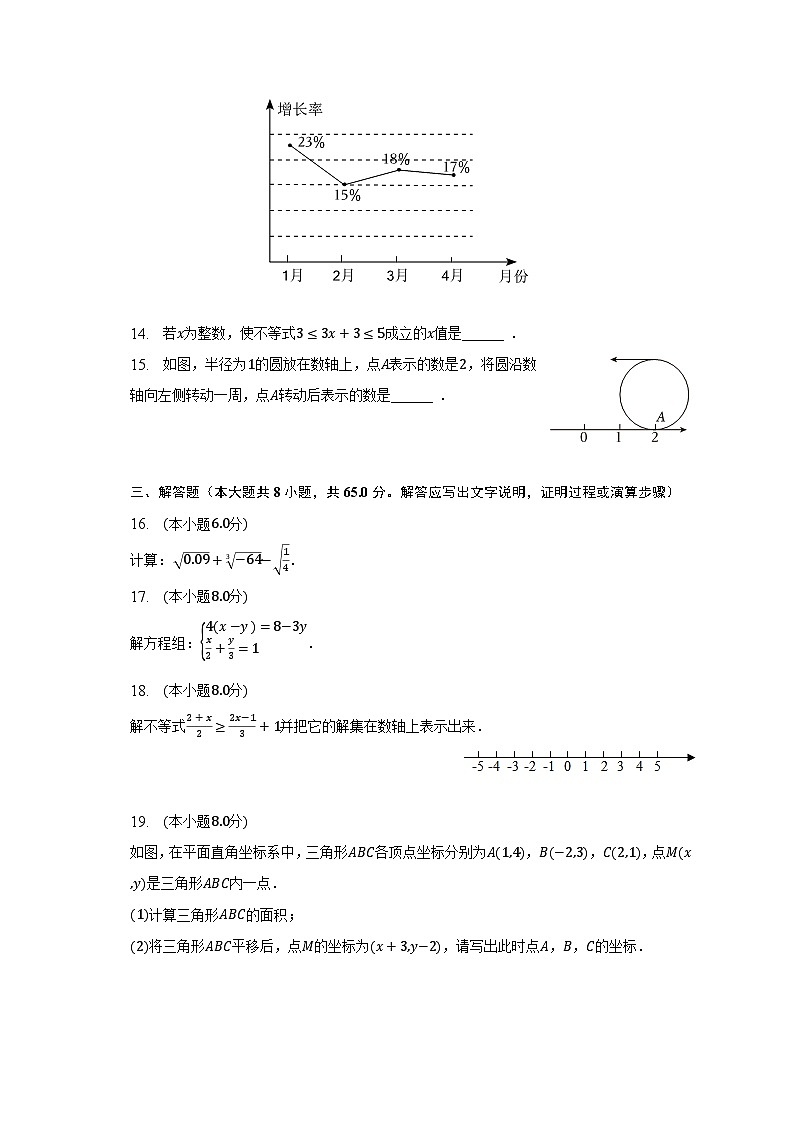
C. 9人
D. 14人
4. 若a A. a−50 C. 12a>12b D. −3a<−3b
5. 解为x=4y=−1的二元一次方程是(    )
A. 2x−y=7 B. 12x+3y=1 C. y−x=5 D. x−2y=6
6. 不等式组3x−1≥−41+2x≤5的解集在数轴上表示正确的是(    )
A. B. C. D.
7. 如图，已知AB//CD//EF，下列结论正确的是(    )
A. ∠BAC=∠DCE
B. ∠BAC=∠CEF
C. ∠BAC+∠ACE=180°
D. ∠BAC+∠ACE+∠CEF=360°
8. 如图，是某班级座位平面图，若小明的座位可以表示为(3,2)，则小华的座位可以表示为(    )
A. (3,5)
B. (4,5)
C. (3,6)
D. (4,6)
9. 某中学要修建一个面积约为80平方米的正方形花圃，它的边长大约是(    )
A. 8.7米 B. 8.8米 C. 8.9米 D. 9.0米
10. 《九章算术》中有一道题，原文是“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之，问几何步及之.”意思是：“同样时间段内，走路快的人能走100步，走路慢的人只能走60步，走路慢的人先走100步，走路快的人走多少步才能追上走路慢的人？”，如果设走路快的人走x步才能追上走路慢的人，走路慢的人又走了y步，根据题意，可列方程组为(    )
A. x=100−yx=60100y B. x−y=100x=60100y C. x−y=100x=10060y D. x=100−yx=10060y
二、填空题（本大题共5小题，共15.0分）
11. 4的平方根是______．
12. 若(3x−y+5)2+|2x−y+3|=0，则x+y=______．
13. 某品牌手机今年1～4月的销售量持续增长，其增长率如图所示，则______ 月份增长率最低．

14. 若x为整数，使不等式3≤3x+3≤5成立的x值是______ ．
15. 如图，半径为1的圆放在数轴上，点A表示的数是2，将圆沿数轴向左侧转动一周，点A转动后表示的数是______ ．


三、解答题（本大题共8小题，共65.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题6.0分)
计算： 0.09+3−64− 14．
17. (本小题8.0分)
解方程组：4(x−y)=8−3yx2+y3=1．
18. (本小题8.0分)
解不等式2+x2≥2x−13+1并把它的解集在数轴上表示出来．

19. (本小题8.0分)
如图，在平面直角坐标系中，三角形ABC各顶点坐标分别为A(1,4)，B(−2,3)，C(2,1)，点M(x,y)是三角形ABC内一点．
(1)计算三角形ABC的面积；
(2)将三角形ABC平移后，点M的坐标为(x+3,y−2)，请写出此时点A，B，C的坐标．

20. (本小题6.0分)
如图，是某同学在学校运动会跳远比赛中留下的脚印，请测量他的成绩.(要求：画出图形，并进行简要说明，按照答题卡测量距离，比例尺1：200计算)

21. (本小题9.0分)
如图1，在一张白纸上画直线a，点P在直线a外；如图2所示，翻折白纸使直线a重合，折痕经过点P，记折痕为直线l；再次如图3所示，翻折白纸，使图2中的直线l重合，经过点P的新的折痕记为直线b；如图4，请根据以上操作说明直线a，b的位置关系，并证明你的结论．


22. (本小题10.0分)
某中学为了更好的开展“读书活动月”活动，向七年级同学推荐一些阅读书目，在活动结束后，对某个班级的学生开展了问卷调查，了解读书活动月期间同学们的每日读书时间，对调查结果进行统计如下：
读书时间(单位：小时)
频数
0～0.5
2
0.5～1
10
1～1.5
12
1.5～2
16
2～2.5
2
根据统计结果解答问题：
(1)补全直方图；
(2)该班级共有多少名学生？
(3)若全校七年级共有420名学生，估计每天读书1～2小时的共有多少人？

23. (本小题10.0分)
学校图书馆购买一批图书，发现有两种套装书特别适合学生阅读.一套是革命家故事丛书共18册，一套是青少年科普读物丛书共20册.若购买3套革命家故事丛书，2套青少年科普读物丛书共需1290元，若购买2套革命家故事丛书，3套青少年科普读物丛书则需要1260元；
(1)若学校预算500元，能否各购买一套丛书？
(2)学校各购买一套丛书以后，发现这两套丛书特别受学生欢迎，打算再次购买.其中革命家故事丛书打算购买其中学生比较喜爱的单册(每册价格相同)，并再购买一套青少年科普读物丛书.此时，书店有促销活动，青少年科普读物丛书全套购买打九折，同时，革命家故事丛书单册购买价格每册书将上浮20%，若学校预算300元，最多可购买几册革命家故事书？
答案和解析

1.【答案】B 
【解析】解：如图，点A的横坐标为1，纵坐标为2，故点A的坐标是(1,2)．
故选：B．
根据点的坐标的定义解答即可．
本题主要考查点的坐标，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．

2.【答案】A 
【解析】解：∵对顶角相等，
∴对顶角量角器测得零件的度数是30°．
故选：A．
由对顶角相等，即可得到答案．
本题考查对顶角，关键是掌握对顶角相等．

3.【答案】C 
【解析】解：设参加艺术社团的学生有x人，
根据题意得：32=x6，
解得：x=9，
∴参加艺术社团的学生有9人．
故选：C．
设参加艺术社团的学生有x人，根据参加文学，艺术两个社团的人数比为2：3，可列出关于x的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．

4.【答案】A 
【解析】解：∵a ∴a−5 ∴选项A符合题意；

∵a ∴a−b<0，
∴选项B不符合题意；

∵a ∴12a<12b，
∴选项C不符合题意；

∵a ∴−3a>−3b，
∴选项D不符合题意．
故选：A．
根据不等式的性质，逐项判断即可．
此题主要考查了不等式的基本性质：(1)不等式的两边同时乘以(或除以)同一个正数，不等号的方向不变；(2)不等式的两边同时乘以(或除以)同一个负数，不等号的方向改变；(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子，不等号的方向不变．

5.【答案】D 
【解析】解：A.把x=4y=−1代入2x−y=7，左边=9≠右边，故本选项不符合题意；
B.把x=4y=−1代入12x+3y=1，左边=−1≠右边，故本选项不符合题意；
C.把x=4y=−1代入y−x=5，左边=−5≠右边，故本选项不符合题意；
D.把x=4y=−1代入x−2y=6，左边=6=右边，故本选项不符合题意．
故选：D．
把x=4y=−1代入各选项的方程，能使方程左右两边相等即是方程的解．
本题考查了二元一次方程的解，一般地，使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解．

6.【答案】C 
【解析】解：3x−1≥−4①1+2x≤5②，
解不等式①，得：x≥−1，
解不等式②，得：x≤2，
∴该不等式组的解集为−1≤x≤2，
其解集在数轴上表示如下所示：
，
故选：C．
先解出每个不等式的解集，即可得到不等式组的解集，然后在数轴上表示出其解集即可．
本题考查解一元一次不等式组、在数轴上表示不等式的解集，解答本题的关键是明确解一元一次不等式的方法．

7.【答案】D 
【解析】解：∵AB//CD//EF，
∴∠BAC+∠ACD=180°，∠DCE+∠CEF=180°，
∴∠BAC+∠ACD+∠DCE+∠CEF=360°，即∠BAC+∠ACE+∠CEF=360°．
故选：D．
利用平行线的性质逐项判断即可．
本题主要考查平行线的性质，熟练掌握平行线的性质是解题关键．平行线性质定理：定理1：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等．定理2：两条平行线被第三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．定理3：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．

8.【答案】D 
【解析】解：由于小明的座位可以表示为(3,2)，则小华的座位可以表示为(4,6)，
故选：D．
根据坐标确定位置的方法进行解答即可．
本题考查坐标确定位置，理解坐标的定义，掌握坐标确定位置的方法是解决问题的关键．

9.【答案】C 
【解析】解：设正方形花圃的边长是x米，
由题意得：x2=80，
∴x= 80=4 5≈8.9，
∴正方形花圃的边长约是8.9米．
故选：C．
设正方形花圃的边长是x米，得到x2=80，于是x= 80=4 5≈8.9．
本题考查算术平方根，关键是掌握算术平方根的定义．

10.【答案】C 
【解析】解：由题意得：
x−y=100x=10060y，
故选：C．
根据“同样时间段内，走路快的人能走100步，走路慢的人只能走60步”和“走路慢的人先走100步，”列方程组求解．
本题考查了由实际问题抽象出二元一次方程组，找到相等关系是解题的关键．

11.【答案】± 2 
【解析】解：∵ 4=2，
∴2的平方根是± 2．
故答案为：± 2．
根据算术平方根和平方根的计算方法进行计算即可得出答案．
本题主要考查了算术平方根和平方根，熟练掌握算术平方根和平方根的计算方法进行求解是解决本题的关键．

12.【答案】−3 
【解析】解：∵(3x−y+5)2+|2x−y+3|=0，∴3x−y+5=0，2x−y+3=0，∴x=−2，y=−1.∴x+y=−3．
根据非负数的性质列出方程，求出x、y的值，再代入求出x+y的值．
本题考查的知识点是：某个数的平方与另一数的绝对值的和等于0，那么平方数的底数为0，绝对值里面的代数式的值为0．

13.【答案】2 
【解析】解：由折线图的数据，可知，2月份增长率最低是15%，
故答案为：2．
根据折线图的数据，可得答案．
考查折线统计图以及增长率的求法，理解增长率的意义是解决问题的前提．

14.【答案】0 
【解析】解：解3≤3x+3得，x≥0，
解3x+3≤5得，x≤23，
∴0≤x≤23，
∵x为整数，
∴x=0．
故答案为：0．
求出不等式组的解集即可求解．
本题考查了一元一次不等式组的解法，熟练掌握一元一次不等式组的解法是解答本题的关键．先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分．不等式组解集的确定方法是：同大取大，同小取小，大小小大取中间，大大小小无解．

15.【答案】2−2π 
【解析】解：由题意得，
该圆的周长为：2×1×π=2π，
∴点A转动后表示的数是2−2π，
故答案为：2−2π．
先计算出该圆的周长，再求得点A转动后表示的数．
此题考查了运用数轴上的点表示实数的应用能力，关键是能准确理解并运用该知识和数形结合思想．

16.【答案】解： 0.09+3−64− 14
=0.3+(−4)−12
=−4.2． 
【解析】首先计算开平方和开立方，然后从左向右依次计算，求出算式的值即可．
此题主要考查了实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．

17.【答案】解：整理得：4x−y=8amp;①3x+2y=6amp;②，
①×2+②，得11x=22，
解得：x=2，
把x=2代入①，得8−y=8，
解得：y=0，
所以方程组的解是x=2y=0． 
【解析】整理后①×2+②得出11x=22，求出x=2，再把x=2代入①求出y即可．
本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键，解二元一次方程组的方法有代入消元法和加减消元法两种．

18.【答案】解：去分母，得：3(2+x)≥2(2x−1)+6，
去括号，得：6+3x≥4x−2+6，
移项，得：3x−4x≥−2+6−6，
合并同类项，得：−x≥−2，
系数化为1，得：x≤2，
将解集表示在数轴上如下：
． 
【解析】根据解一元一次不等式基本步骤：去分母，去括号、移项、合并同类项、系数化为1可得．
本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．

19.【答案】解：(1)△ABC的面积=3×4−12×1×3−12×1×3−12×2×4=5；
(2)把A，B，C的横坐标加3.纵坐标减2，可得此时点A，B，C的坐标分别为(4,2)，(1,1)，(5,−1)． 
【解析】(1)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可；
(2)利用平移变换的规律解决问题．
本题考查作图−平移变换，解题的关键是学会用分割法求三角形面积，掌握平移变换的性质．

20.【答案】解：如图，测量垂线段AB的长即可，依据为垂线段最短，

3×200=600(cm)=6(m)，
答：成绩为6m． 
【解析】利用垂线段最短及比例尺计算即可求解．
本题考查了垂线段：从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段．关键是掌握垂线段的性质：垂线段最短．

21.【答案】解：a//b.理由如下：
设点A的对应点为A′，
则直线l为对称轴，
AA′与直线l交于点N．
设点B的对应点为B′，
则直线b为对称轴，
BB′与直线b交于点M．

根据折叠的性质，
得∠ANC=∠ANC，
又∵∠ANC+∠A′NC=180°，
∴∠ANC=90°．
同理可得∠BMD=90°．
∴∠ANC=∠B′MD．
∴a//b． 
【解析】设点A的对应点为A，直线l为对称轴，AA与直线l交于点N；设点B的对应点为B′，直线b为对称轴，BB′与直线b交于点M；根据折叠的性质可求得∠ANC=∠BMM=90°，即可判断直线a，b的位置关系．
本题主要考查折叠的性质和平行线的判定，牢记折叠的性质和平行线的判定定理是解题的关键．

22.【答案】解：(1)补全直方图如下：

(2)2+10+12+16+2=42(名)，
答：该班级共有42名学生；
(3)420×12+1642=280(人)，
答：估计每天读书1～2小时的共有280人． 
【解析】(1)根据频数分布表的数据即可补全直方图；
(2)把各组频数相加即可；
(3)用七年级总人数乘样本中每天读书1～2小时的频率即可．
本题考查频数分布表，用样本估计总体以及频数分布直方图，掌握“频率=频数÷总数”是正确解答的前提．

23.【答案】解：(1)设购买一套革命家故事丛书需要x元，购买一套青少年科普读物丛书需要y元，
由题意得：3x+2y=12902x+3y=1260，
解得：x=270y=240，
∴x+y=270+240=510，
∵500<510，
∴若学校预算500元，不能各购买一套丛书，
答：若学校预算500元，不能各购买一套丛书；
(2)设可购买m册革命家故事书，
由题意得：27018(1+20%)m+240×0.9≤300，
解得：m≤423，
∵m为正整数，
∴m的最大值为4，
答：若学校预算300元，最多可购买4册革命家故事书． 
【解析】(1)设购买一套革命家故事丛书需要x元，购买一套青少年科普读物丛书需要y元，根据若购买3套革命家故事丛书，2套青少年科普读物丛书共需1290元，若购买2套革命家故事丛书，3套青少年科普读物丛书则需要1260元；列出二元一次方程组，解方程组即可；
(2)设可购买m册革命家故事书，学校预算300元，列出一元一次不等式，解不等式即可．
本题考查了二元一次方程组的应用、一元一次不等式的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组；(2)找出数量关系，正确列出一元一次不等式．