

2023年吉林省松原市宁江区油田十二中中考数学五模试卷(含解析)
展开2023年吉林省松原市宁江区油田十二中中考数学五模试卷
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
1. −2的相反数是( )
A. 2 B. −2 C. 12 D. −12
2. 今年五一小长假期间,长春某景区接待游客约为81600人次,数字81600用科学记数法表示为( )
A. 0.816×105 B. 8.16×104 C. 8.16×105 D. 81.6×103
3. 如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B. C. D.
4. 关于x的不等式组的解集在数轴上表示如图所示,则不等式组解集为( )
A. −2≤x≤1 B. −2≤x<1 C. −2
A. 两点确定一条直线
B. 三角形内角和是180°
C. 等腰三角形底边上的中线和与底边上的高重合
D. 垂线段最短
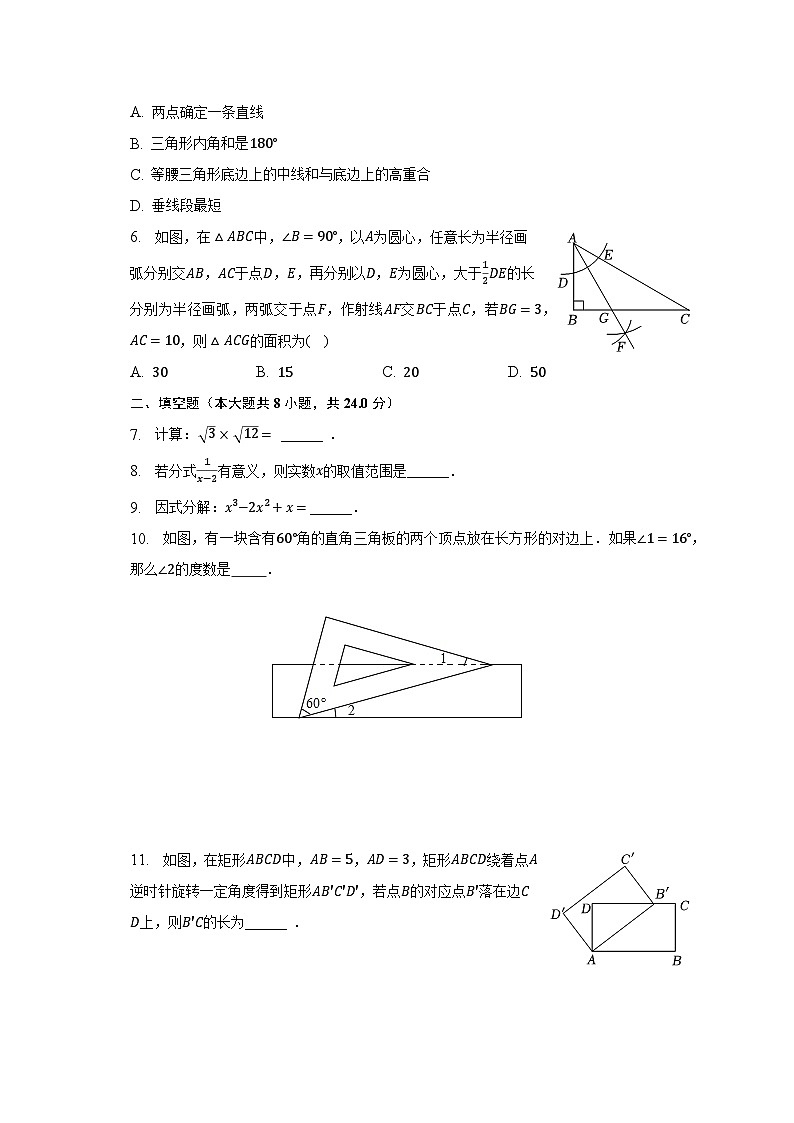
6. 如图,在△ABC中,∠B=90°,以A为圆心,任意长为半径画弧分别交AB,AC于点D,E,再分别以D,E为圆心,大于12DE的长分别为半径画弧,两弧交于点F,作射线AF交BC于点C,若BG=3,AC=10,则△ACG的面积为( )
A. 30 B. 15 C. 20 D. 50
二、填空题(本大题共8小题,共24.0分)
7. 计算: 3× 12= ______ .
8. 若分式1x−2有意义,则实数x的取值范围是______.
9. 因式分解:x3−2x2+x=______.
10. 如图,有一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=16°,那么∠2的度数是 .
11. 如图,在矩形ABCD中,AB=5,AD=3,矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB′C′D′,若点B的对应点B′落在边CD上,则B′C的长为______ .
12. 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为______.
13. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为______ 米.
14. 如图,矩形ABCD内接于圆中.若AB= 3cm,BC=1cm,则阴影部分图形的面积是______ cm2(结果保留π).
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题5.0分)
先化简,再求值:(2a+1)2−4a(a−1)+2,其中a=18.
16. (本小题5.0分)
如图,点A、B、D、E在同一条直线上,AB=DE,AC//DF,BC//EF.求证:BC=EF.
17. (本小题5.0分)
某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品.如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率.(请用“画树状图”或“列表”等方法写出分析过程)
18. (本小题5.0分)
某车间接到加工960个零件的任务,在加工完160个后,由于改进了技术,每天加工的零件数量是原来的5倍,整个加工过程共用了4天完成.求原来每天加工零件的数量.
19. (本小题7.0分)
如图,在6×6的网格中,△ABC的三个顶点都在格点上,请画出符合下列条件的图形.
(1)在图1中画出格点D(不与点B重合),连接AD、CD,使△ACD与△ABC全等.
(2)在图2中画出格点E,连接BE、CE,使△EBC的面积等于△ABC面积的2倍.
(3)在图3中,在线段AC上取点F,连接BF,使BF平分△ABC面积.
20. (本小题7.0分)
如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米)
【参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51】
21. (本小题7.0分)
为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七、八年级部分学生的分数,过程如下:
(1)收集数据.
从该校七、八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
(2)整理、描述数据.
按下表分段整理描述样本数据:
分数x
人数
年级
80≤x<85
85≤x<90
90≤x<95
95≤x≤100
七年级
4
6
2
8
八年级
3
a
4
7
(3)分析数据.
两组样本数据的平均数中位数、众数、方差如表所示:
年级
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
b
c
33.2
根据以上提供的信息,解答下列问题:
①填空:a= ______ ,b= ______ ,c= ______ ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分,______ 同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”);
③从样本数据分析来看,分数较整齐的是______ 年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有______ 人的分数不低于95分.
22. (本小题7.0分)
如图,反比例函数y=kx的图象与正比例函数y=14x的图象交于点A(m,−1)和B(4,n),点P(1,b)在反比例函数y=kx的图象上.
(1)求反比例函数的解析式和点P的坐标.
(2)直接写出不等式kx>14x的解集.
(3)连接OP,直接写出△BOP的面积.
23. (本小题8.0分)
某种机器是在油箱加满的状态下开始工作,当停止工作时,油箱中油量为5L.在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)机器里每分钟加油量为______ L,机器工作的过程中每分钟耗油量为______ L.
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
(3)直接写出油箱中油量为油箱容积的一半时x的值.
24. (本小题8.0分)
定义:有一组邻边相等且对角互补的四边形叫做等补四边形,
【理解】
(1)如图1,点A、B、C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD、CD.则四边形ABCD是等补四边形.
请直接写出图中相等的边:______ ;互补的角:______ .
【探究】
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.
【运用】
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,直接写出DF的长.
25. (本小题10.0分)
如图,在菱形ABCD中,AB=4cm,∠DAB=60°,点P从点A出发,以2cm/s的速度沿A−D−C运动,过点P作射线AB的垂线,交射线AB于点Q,在点P运动过程中,设运动时间为t(s),△APQ与菱形ABCD重叠部分的面积为S(cm2).
(1)写出线段PD的长(用含t的式子表示).
(2)当PQ平分菱形面积时,求t的值.
(3)求S与t的函数关系式,并写出自变量的取值范围.
26. (本小题10.0分)
如图,在平面直角坐标系中,抛物线y=−x2+bx+c与x轴和y轴分别交于点A(3,0)和点B(0,3),点P是此抛物线上一点,其横坐标为m.
(1)求抛物线的解析式.
(2)若点P在x轴上方的抛物线上时,请结合图象直接写出x的取值范围.
(3)过点P作PQ//x轴,点Q的横坐标为−m+1,点P与点Q不重合.
①当线段PQ的长度随m的增大而减小,求m的取值范围.
②在PQ的下方作等腰直角三角形QPR,且∠QPR=90°,当−2≤m≤2时,直接写出等腰直角三角形QPR与抛物线的交点个数及m的取值范围.
答案和解析
1.【答案】A
【解析】解:−2的相反数是2.
故选:A.
利用相反数的定义判断即可.
此题考查了相反数,熟练掌握相反数的定义是解本题的关键.
2.【答案】B
【解析】解:数字81600用科学记数法表示为8.16×104.
故选:B.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.【答案】C
【解析】解:将圆柱侧面沿AC“剪开”,侧面展开图为矩形,
∵圆柱的底面直径为AB,
∴点B是展开图的一边的中点,
∵蚂蚁爬行的最近路线为线段,
∴C选项符合题意,
故选:C.
利用圆柱的侧面展开图是矩形,而点B是展开图的一边的中点,再利用蚂蚁爬行的最近路线为线段可以得出结论.
本题主要考查了圆柱的侧面展开图,最短路径问题,掌握两点之间线段最短是解题的关键.
4.【答案】B
【解析】解:关于x的不等式组的解集在数轴上表示如图所示,
则不等式组解集为−2≤x<1,
故选:B.
根据数轴上表示的解集确定出所求即可.
此题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
5.【答案】C
【解析】解:∵△ABC是等腰直角三角形,
∴AC=BC,
∵AO=BO,
∴OC⊥AB,
∵OC垂直于地面,
∴OC平行于地面,
∴房梁是水平的,
∴其数学道理是:等腰三角形底边上的中线和与底边上的高重合.
故选:C.
由等腰三角形的性质:等腰三角形底边上的中线和与底边上的高重合,即可得到答案.
本题考查等腰三角形的性质,关键是掌握等腰三角形的性质.
6.【答案】B
【解析】解:由作法得AG平分∠BAC,
∴G点到AC的距离等于BG的长,即G点到AC的距离为3,
所以△ACG的面积=12×3×10=15.
故选:B.
利用基本作图得到AG平分∠BAC,利用角平分线的性质得到G点到AC的距离为3,然后根据三角形面积公式计算△ACG的面积.
本题考查了作图−基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了角平分线的性质.
7.【答案】6
【解析】解: 3× 12= 3×2 3=2×3=6.
故答案为:6.
利用二次根式的运算法则计算即可.
本题考查了二次根式的乘除运算,解题的关键是掌握二次根式的乘法运算法则.
8.【答案】x≠2
【解析】解:∵x−2≠0,
∴x≠2.
故答案为:x≠2.
根据分式的分母不等于0即可得出答案.
本题考查了分式有意义的条件,掌握分式的分母不等于0是解题的关键.
9.【答案】x(x−1)2
【解析】解;x3−2x2+x=x(x2−2x+1)=x(x−1)2,
故答案为:x(x−1)2.
先提公因式x,再利用完全平方公式,即可解答.
本题考查了提公因式法和公式法进行因式分解,解决本题的关键是熟记提公因式法和公式法.
10.【答案】14°
【解析】
【分析】
先利用互余得到∠3=14°,然后根据平行线的性质求∠2的度数.
本题考查了平行线性质,掌握两直线平行,内错角相等是解题的关键.
【解答】
解:∵∠1+∠3=90°−60°=30°,
而∠1=16°,
∴∠3=14°,
∵a//b,
∴∠2=∠3=14°.
故答案为14°.
11.【答案】1
【解析】解:∵矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB′C′D′,
∴AB=AB′=5,AB=CD=5,
∵∠D=90°,
∴B′D= B′A2−AD2= 25−9=4,
∴B′C=CD−B′D=1,
故答案为:1.
由旋转的性质可得AB=AB′=5,AB=CD=5,由勾股定理可求B′D的长,即可求解.
本题考查了旋转的性质,矩形的判定和性质,勾股定理,掌握旋转的性质是解题的关键.
12.【答案】80°
【解析】解:∵在⊙O中,AB为直径,BC为弦,CD为切线,
∴∠OCD=90°,
∵∠BCD=50°,
∴∠OCB=40°,
∴∠AOC=80°.
故答案为:80°.
根据切线的性质得出∠OCD=90°,进而得出∠OCB=40°,再利用圆心角等于圆周角的2倍解答即可.
本题考查了切线的性质定理以及圆周角定理的运用,熟记和圆有关的各种性质定理是解题关键.
13.【答案】3
【解析】解:由题意知:AB//CD,
则∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴ABCD=AECE,
∴1CD=0.41.6−0.4,
∴CD=3米,
故答案为:3.
由题意知:△ABE∽△CDE,得出对应边成比例即可得出CD.
本题考查了相似三角形的判定与性质,根据题意得出△ABE∽△CDE是解决问题的关键.
14.【答案】2π3− 32
【解析】解:连接CA,BD,交于O,
∵四边形ABCD是矩形,
∴∠ABC=∠DAB=90°,
∴AC,BD是圆的直径,
∴O是圆的圆心,
∵AB= 3cm,BC=1cm,
∴AC= AB2+BC2=2(cm),
∵tan∠ADB=ABAD= 3,
∴∠ADB=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴扇形OAD的面积=60π×12360=π6(cm2),
∴扇形OBC的面积=扇形OAD的面积=π6(cm2),
∵矩形ABCD的面积=AB⋅AD= 3(cm2),
∴△OAB的面积=△ODC的面积=14×矩形ABCD的面积= 34(cm2),
∵圆的面积=π×12=π(cm2),
∴阴影的面积=圆的面积−扇形OAD的面积×2−△OAB的面积×2=π−π3− 32=(2π3− 32)(cm2).
故答案为:(2π3− 32).
连接CD,BD,交于O,由圆周角定理得到AC,BD是圆的直径,由锐角的正切求出∠ADB的度数,求出扇形OAD的面积,△OAB的面积,即可求出阴影的面积.
本题考查扇形面积的计算,矩形的性质,圆周角定理,解直角三角形,关键是由锐角的正切定义求出∠ADB=60°,求出扇形OAD的面积.
15.【答案】解:(2a+1)2−4a(a−1)+2
=4a2+4a+1−4a2+4a+2
=8a+3,
当a=18时,原式=8×18+3
=1+3
=4.
【解析】先去括号,再合并同类项,然后把a的值代入化简后的式子进行计算,即可解答.
本题考查了整式的混合运算−化简求值,完全平方公式,准确熟练地进行计算是解题的关键.
16.【答案】证明:∵AC//DF,BC//EF,
∴∠A=∠FDE,∠CBA=∠E,
∵AB=DE,
∴△ABC≌△DEF(ASA),
∴BC=EF.
【解析】利用平行线的性质可得∠A=∠FDE,∠CBA=∠E,从而利用ASA证明△ABC≌△DEF,然后利用全等三角形的性质即可解答.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
17.【答案】解:画树状图为:
共有12种等可能的结果数,其中两次摸到红球的结果数为2,
所以小芳获得2份奖品的概率=212=16.
【解析】画树状图展示所有12种等可能的结果数,找出两次摸出的球是红球的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.
18.【答案】解:设原来每天加工x个零件,则改进技术后每天加工5x个零件,
依题意,得:160x+960−1605x=4,
解得:x=80,
经检验,x=80是原分式方程的解,且符合题意.
答:原来每天加工80个零件.
【解析】设原来每天加工x个零件,则改进技术后每天加工5x个零件,根据工作时间=工作总量÷工作效率,即可得出关于x的分式方程,解之经检验后即可得出结论.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
19.【答案】解:如图:
(1)如图1,点D即为所求;
(2)如图2,点E即为所求;
(3)如图3,点F即为所求.
【解析】(1)根三角形全等是判定定理作图;
(2)根据三角形的面积公式作图;
(3)根据三角形中位线的性质作图.
本题考查了作图的应用与设计,掌握三角形全等的判定定理、三角形的面积公式及中位线的性质是解题的关键.
20.【答案】解:如图,在△ABE中,有BE=tan27°×AE=0.51×78=39.78(米),
故BD=ED+BE=34+39.78≈73.8(米).
答:乙楼的高度约为73.8米.
【解析】首先分析图形:根据题意构造直角三角形△ABE,解其可得BE的长,进而借助BD=ED+BE可解即可求出答案.
此题考查的知识点是解直角三角形的应用−仰角俯角问题,关键是本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
21.【答案】①6; 91; 95
②甲
③八
④160
【解析】解:①∵七、八年级学生中各随机抽取20名学生的分数,
∴a=20−3−4−7=6,
八年级学生的成绩从低到高排列,第10,11名学生的成绩为90分,92分,
∴b=90+922=91(分),
八年级成绩的95分出现了3次,次数最多,
∴c=95,
故答案为:6,91,95;
②甲同学的分数在本年级抽取的分数中从高到低排序更靠前,理由如下:
∵八年级的中位数是91分,七年级的中位数是89分,
∴90分大于七年级成绩的中位数,而小于八年级成绩的中位数,
∴七年级甲同学的分数在本年级抽取的分数中从高到低排序更靠前;
故答案为:甲;
③∵八年级成绩的方差小于七年级成绩的方差,
∴分数较整齐的是八年级,
故答案为:八;
④因为七年级不低于95分的有8人,
所以400×820=160(人),
故答案为:160.
(1)根据七、八年级学生中各随机抽取20名学生的分数可得a=6,第10,11名学生的成绩为90分,92分,即可求出b的值,95分出现了3次,次数最多,可得c的值;
(2)根据八年级的中位数是91分,七年级的中位数是89分,可得90分大于七年级成绩的中位数,而小于八年级成绩的中位数,进而可得结论;
(3)根据方差进行评价即可作出判断;
(4)用七年级不低于95分的比例乘以总人数即可.
本题考查频数分布表、用样本估计总体、方差、中位数、众数的意义及求法,理解各个统计量的意义,明确各个统计量的特点是解决问题的前提和关键.
22.【答案】解:(1)把点A(m,−1)和B(4,n)代入y=14x得,−1=14m,n=14×4,
∴m=−4,n=1,
∴点A(−4,−1),B(4,1),
∵反比例函数y=kx的图象与正比例函数y=14x的图象交于点A(−4,−1)和B,
∴k=−4×(−1)=4,
∴反比例函数的解析式为y=4x,
∵点P(1,b)在反比例函数的图象上.
∴b=41=4,
∴P(1,4);
(2)由图象可知:不等式kx>14x的解集0
∵P(1,4),
∴PN=4−14=154,
∴S△POB=S△PON+S△PBN=12×154×1+12×154×3=158+458=152.
【解析】(1)由正比例函数的解析式求得A、B的坐标,即可求得反比例函数的解析式,把点P(1,b)代入即可求得P的坐标;
(2)根据图象和两个函数交点的坐标直接写出即可;
(3)过点P作x轴的垂线PM,交OB于点N.则N(1,14),根据S△POB=S△PON+S△PBN计算即可.
本题考查了一次函数图象上点的坐标特征,待定系数法求反比例函数的解析式,三角形的面积,求得交点坐标是解题的关键.
23.【答案】3 0.5
【解析】解:(1)由图象可得,
机器每分钟加油量为:30÷10=3(L),
机器工作的过程中每分钟耗油量为:(30−5)÷(60−10)=0.5(L),
故答案为:3,0.5;
(2)当10
解得,a=−0.5b=35,
即机器工作时y关于x的函数解析式为y=−0.5x+35(10
当−0.5x+35=30÷2时,得x=40,
即油箱中油量为油箱容积的一半时x的值是5或40.
(1)根据函数图象中的数据,可以得到机器每分钟加油量和机器工作的过程中每分钟耗油量;
(2)根据函数图象中的数据,可以得到机器工作时y关于x的函数解析式,并写出自变量x的取值范围;
(3)根据(2)中的函数解析式和(1)中的加油的速度,令函数值为30÷2,即可得到相应的x的值.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
24.【答案】AD=CD ∠A与∠C,∠BAC与∠ADC
【解析】解:(1)如图1,
连接AC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠CAD=∠CBD,∠ACD=∠ABD,
∴∠ACD=∠CAD,
∴AD=CD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°,∠ABC+∠ADC=180°,
故答案为:AD=CD,∠A+∠C=180°(原图中),∠ABC+∠ADC=180°;
(2)如图2,
AC平分∠BCD,理由如下:
∵四边形ABCD是等补四边形,
∴四边形ABCD内接于圆,
连接BD,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ACD=∠ABD,∠ACB=∠ADB,
∴∠ACD=∠ACB,
∴AC平分∠BCD;
(3)如图3,
连接AC,
由(2)知:四边形ABCD内接于圆,AC平分∠BCD,
∴∠DAE=∠BCD,∠ACD=12∠BCD,
∵AF平分∠DAE,
∴∠DAF=12∠DAE,
∴∠DAE=∠ACD,
∵∠F=∠F,
∴△AFD∽△CFA,
∴AFCF=DFAF,
∴CF⋅DF=AF2,
∴DF⋅(DF+CD)=25,
∴DF(DF+10)=25,
∴DF1=5 2−5,DF2=−5 2−5(舍去),
∴DF=5 2−5.
(1)连接AC,可推出∠ABD=∠CBD,∠CAD=∠CBD,∠ACD=∠ABD,∠ACD=∠CAD,从而AD=CD,根据四边形ABCD是⊙O的内接四边形,可得出∠BAD+∠BCD=180°,∠ABC+∠ADC=180°;
(2)连接BD,可推出四边形ABCD内接于圆,∠ABD=∠ADB,∠ACD=∠ABD,∠ACB=∠ADB,从而∠ACD=∠ACB,从而AC平分∠BCD;
(3)连接AC,可推出∠DAE=∠ACD,进而得出△AFD∽△CFA,从而AFCF=DFAF,进而得出DF⋅(DF+CD)=25,从而求得DF.
本题考查了确定圆的条件,等腰三角形的判定和性质,圆周角定理的推论,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握有关基础知识.
25.【答案】解:(1)∵四边形ABCD是菱形,
∴AB=AD=DC=4cm,
当0
∴DP=MQ,
∵AD=AB=4cm,∠DAB=60°,
∴AM=2cm,
∵PQ平分菱形的面积,
∴PQ经过BD的中点O,
∴OB=OD,
∵四边形ABCD是菱形,
∴DC//AB,
∴∠PDO=∠OBQ,∠DPO=∠BQO,
∴△DPO≌△BQO(AAS),
∴DP=BQ=(2t−4)cm,
∴2+2t−4+2t−4=4,
∴t=52;
(3)分三种情况:①当0
∵AP=2t cm,∠A=60°,
∴AQ=12AP=tcm,PQ= 3t cm,
∴S△APQ=12AQ⋅PQ=12×t× 3t= 32t2,
∴S= 32t2;
②当2
由(2)可知,PQ=2 3cm,
∵DP=(2t−4)cm,
∴AQ=2+2t−4=(2t−2)cm,
∴S=S△APQ=12AQ⋅PQ=12×2 3×(2t−2)=2 3t−2 3;
S=12(2+2t−4)×2 3=2 3t−2 3;
③当3
∵AQ=(2t−2)cm,AB=4cm,
∴BQ=(2t−6)cm,
∵∠QBN=60°,
∴QN= 3BQ= 3(2t−6)(cm),
∴S=S△AQP−S△BQN=2 3t−2 3−12(2t−6)⋅ 3(2t−6)
=−2 3t2+14 3t−20 3.
综上所述,S与t的函数关系式为S= 32t2(0
(3)分三种情况:①当0
26.【答案】解:(1)把A(3,0)和B(0,3)代入y=−x2+bx+c得:
−9+3b+c=0c=3,
解得b=2c=3,
∴抛物线的解析式为y=−x2+2x+3;
(2)在y=−x2+2x+3中,令y=0得:0=−x2+2x+3,
解得x=−1或x=3,
由图可得,点P在x轴上方的抛物线上时,x的取值范围是−1
∴当m=−m+1,即m=12时,P与Q重合;
当m<−m+1,即m<12时,PQ=−m+1−m=−2m+1,
此时PQ随m的增大而减小,符合题意;
当−m+1
此时PQ随m的增大而增大,不符合题意;
综上所述,当线段PQ的长度随m的增大而减小,m的取值范围是m<12;
②由①知,当m=12时,P,Q重合,
当−2≤m<12时,P在Q的左侧,如图:
此时等腰直角三角形QPR与抛物线的交点只有1个;
∵y=−x2+2x+3=−(x−1)2+4,
∴抛物线y=−x2+2x+3的对称轴为直线x=1,
当12
由图可知,此时等腰直角三角形QPR与抛物线的交点有2个;
当1
此时等腰直角三角形QPR与抛物线的交点有3个;
综上所述,当−2≤m<12时,等腰直角三角形QPR与抛物线的交点有1个;当12
(2)求出y=0时x=−1或x=3,由图可得x的取值范围是−1
②由①知,当m=12时,P,Q重合,分3种情况:当−2≤m<12时,当12
2023-2024学年吉林省松原市宁江区吉林油田十二中八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年吉林省松原市宁江区吉林油田十二中八年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年吉林省松原市宁江区油田十二中七年级(上)期中数学试卷(含解析): 这是一份2023-2024学年吉林省松原市宁江区油田十二中七年级(上)期中数学试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年吉林省松原市宁江区中考数学三模试卷(含解析): 这是一份2023年吉林省松原市宁江区中考数学三模试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












