2022-2023学年福建省泉州市鲤城区科技中学八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年福建省泉州市鲤城区科技中学八年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年福建省泉州市鲤城区科技中学八年级（下）期中数学试卷
一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）
1. 计算：30=(    )
A. −3 B. 1 C. 3 D. −1
2. 若分式8x−1有意义，则实数x的取值范围是(    )
A. x>1 B. xy2>y3 B. y3>y2>y1 C. y1>y3>y2 D. y2>y1>y3
6. 如果把分式2x3x−2y中的x和y都扩大3倍，那么分式的值(    )
A. 扩大3倍 B. 扩大9倍 C. 缩小3倍 D. 不变
7. 已知一次函数y=ax+a+2的图象与y轴的正半轴相交，且y随x的增大而减小，则a的值可以是(    )
A. 14 B. −1 C. −2 D. 12
8. 如图，EF 过平行四边形ABCD对角线的交点O，交AD于E，交BC于F，若平行四边形ABCD的周长为18，OE=1.5，则四边形EFCD的周长为(    )

A. 14 B. 13 C. 12 D. 10
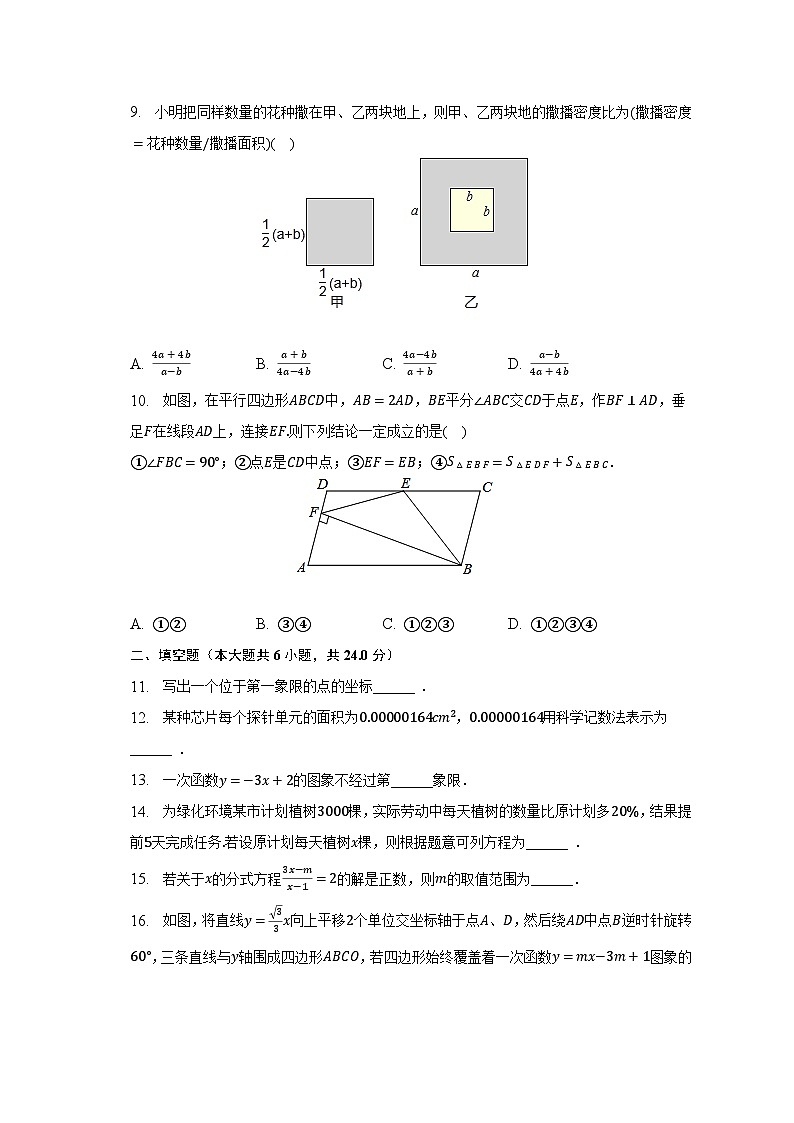
9. 小明把同样数量的花种撒在甲、乙两块地上，则甲、乙两块地的撒播密度比为(撒播密度=花种数量/撒播面积)(    )

A. 4a+4ba−b B. a+b4a−4b C. 4a−4ba+b D. a−b4a+4b
10. 如图，在平行四边形ABCD中，AB=2AD，BE平分∠ABC交CD于点E，作BF⊥AD，垂足F在线段AD上，连接EF.则下列结论一定成立的是(    )
①∠FBC=90°；②点E是CD中点；③EF=EB；④S△EBF=S△EDF+S△EBC．

A. ①② B. ③④ C. ①②③ D. ①②③④
二、填空题（本大题共6小题，共24.0分）
11. 写出一个位于第一象限的点的坐标______ ．
12. 某种芯片每个探针单元的面积为0.00000164cm2，0.00000164用科学记数法表示为______ ．
13. 一次函数y=−3x+2的图象不经过第______象限．
14. 为绿化环境某市计划植树3000棵，实际劳动中每天植树的数量比原计划多20%，结果提前5天完成任务.若设原计划每天植树x棵，则根据题意可列方程为______ ．
15. 若关于x的分式方程3x−mx−1=2的解是正数，则m的取值范围为______．
16. 如图，将直线y= 33x向上平移2个单位交坐标轴于点A、D，然后绕AD中点B逆时针旋转60°，三条直线与y轴围成四边形ABCO，若四边形始终覆盖着一次函数y=mx−3m+1图象的一部分，则满足条件的实数m的取值范围为          ．







三、解答题（本大题共9小题，共86.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题8.0分)
计算：(3−2 3)0+2−2+|−2|×(−1)2023．
18. (本小题8.0分)
解方程：xx−1−2=32x−2．
19. (本小题8.0分)
一次函数y=kx−2的图象经过点(1,−3)．
(1)求这个一次函数的表达式；
(2)当x为何值时，y>0？
20. (本小题8.0分)
如图，在▱ABCD中，点E、F在直线AC上，且AE=CF，求证：四边形DEBF是平行四边形．

21. (本小题8.0分)
有夫妻两人在为某公司生产A、B两种型号的零件，丈夫负责生产A型零件，妻子负责生产B型零件，已知丈夫生产120个A型零件所用时间是妻子生产80个B型零件所用时间的2倍，夫妻两人每天共生产35个零件.生产一个A型零件的工资为15元，生产一个B型零件的工资为8元，求夫妻两人一天的总收入．
22. (本小题10.0分)
观察下列等式：
第1个等式：31×2×22=11×2−12×22；
第2个等式：42×3×23=12×22−13×23；
第3个等式：53×4×24=13×23−14×24；
第4个等式：64×5×25=14×24−15×25；
第5个等式：75×6×26=15×25−16×26；
……
按上述规律，回答以下问题：
(1)写出第6个等式：______；
(2)写出你猜想的第n个等式：______(用含n的等式表示)，并证明．
23. (本小题10.0分)
如图，在平面直角坐标系中，一次函数y=kx+b的图象经过点A(−2,6)，且与x轴相交于点B，与正比例函数y=3x的图象相交于点C，点C的横坐标为1．
(1)求k、b的值；
(2)若点D在y轴负半轴上，且满足S△COD=13S△BOC，求点D的坐标．

24. (本小题12.0分)
如图，在▱ABCD中，点E为BC上一点，连接AE并延长交DC的延长线于点F，AD=DF，连接DE．
(1)求证：AE平分∠BAD；
(2)若点E为BC中点，∠B=60°，AD=4，求▱ABCD的面积．

25. (本小题14.0分)
如图1，在平面直角坐标系中，直线l：y=34x+32与x轴交于点A，且经过点B(2,m)、点C(3,0)．
(1)求直线BC的函数解析式；
(2)在线段BC上找一点D，使得△ABO与△ABD的面积相等，求出点D的坐标；
(3)y轴上有一动点P，直线BC上有一动点M，若△APM是以∠AMP为直角的等腰直角三角形，求出点M的坐标．


答案和解析

1.【答案】B 
【解析】解：30=1，
故选：B．
根据零指数幂计算即可．
本题考查了零指数幂，认准0次幂的底数是3是解题的关键．

2.【答案】C 
【解析】解：由题意得：x−1≠0，
解得：x≠1，
故选：C．
根据分式有意义的条件可得x−1≠0，再解即可．
此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．

3.【答案】B 
【解析】解：原式=ac⋅cac⋅ab=cab．
故选：B．
由原式得到原式=ac⋅cac⋅ab，然后分子分母都约去ac即可．
本题考查了分式的乘法：ba⋅dc=bdac.也考查了约分．

4.【答案】B 
【解析】解：∵点P(−20,a)与点Q(b,13)关于x轴对称，
∴b=−20，a=−13，
∴a+b=−20+(−13)=−33，
故选：B．
根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得a、b的值，进而得到a+b．
此题主要考查了关于x轴对称点的坐标，关键是掌握点的坐标的变化规律．

5.【答案】B 
【解析】解：∵k=2>0，
∴y随x的增大而增大，
又∵点A(−2,y1)，B(−1,y2)，C(3,y3)在一次函数y=2x−3的图象上，且−2y1．
故选：B．
由k=2>0，利用一次函数的性质，可得出y随x的增大而增大，再结合−2y1．
本题考查了一次函数的性质，牢记“k>0，y随x的增大而增大；k0得a>−2，
∵图象y随x的增大而减小，
∴a