2022-2023学年福建省宁德市七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年福建省宁德市七年级（下）期末数学试卷（含解析），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年福建省宁德市七年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 书法是我国传统文化的重要组成部分，被誉为：无言的诗，无形的舞，无图的画，无声的乐.下列是用小篆书写的“魅力宁德”四个字，其中是轴对称图形的是(    )
A. B. C. D.
2. 唐诗“不经一番寒彻骨，怎得梅花扑鼻香.”歌颂了梅花不畏严寒，努力绽放的坚毅品格.已知某种梅花花粉的直径约为0.000032米，数据0.000032用科学记数法表示为(    )
A. 0.32×10−4 B. 3.2×10−4 C. 3.2×10−5 D. 32×10−6
3. 如果一个三角形的两边长分别为3，8，则第三边的长可以是(    )
A. 5 B. 10 C. 11 D. 12
4. 如图，AE是△ABC的中线，点D是BE上一点，若BD=5，CD=9，则CE的长为(    )
A. 5
B. 6
C. 7
D. 8
5. 下列式中计算结果是x6的是(    )
A. x3+x3 B. x8−x C. x4⋅x2 D. (−x2)3
6. 如图，AB⊥BC于点B，BD⊥AC于点D，则下列表示点A到BD的距离的是(    )
A. 线段AD的长
B. 线段BD的长
C. 线段AB的长
D. 线段CD的长
7. 如图1，将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分)，并将剩余部分沿虚线剪开，得到两个长方形，再将这两个长方形拼成一个如图2所示的大长方形.比较两个图形，能验证的等式是(    )

A. x(x−1)=x2−x B. (x−1)2=x2−2x+1
C. (x+1)2=x2+2x+1 D. (x+1)(x−1)=x2−1
8. 掷一枚质地均匀的骰子.小明掷了3次，其中2次点数为5，1次点数为2.若他再掷1次，则点数为5的概率是(    )
A. 0 B. 16 C. 13 D. 23
9. 已知△ABC，求作：Δ A′B′C′，使得Δ A′B′C′≌△ABC.如图是小明的作图痕迹，他作图的依据是(    )

A. SSS B. AAS C. ASA D. SAS
10. 若(m+1)2=3，(n+1)2=5，则(n+m+2)(n−m)=(    )
A. −2 B. 2 C. 4 D. 15
二、填空题（本大题共6小题，共18.0分）
11. (13)−1=______．
12. 已知∠1与∠2互补.若∠1=50°，则∠2= ______ °.
13. “小明投篮一次，投进篮筐”，这一事件是______事件．(填“随机”或“必然”或“不可能”)
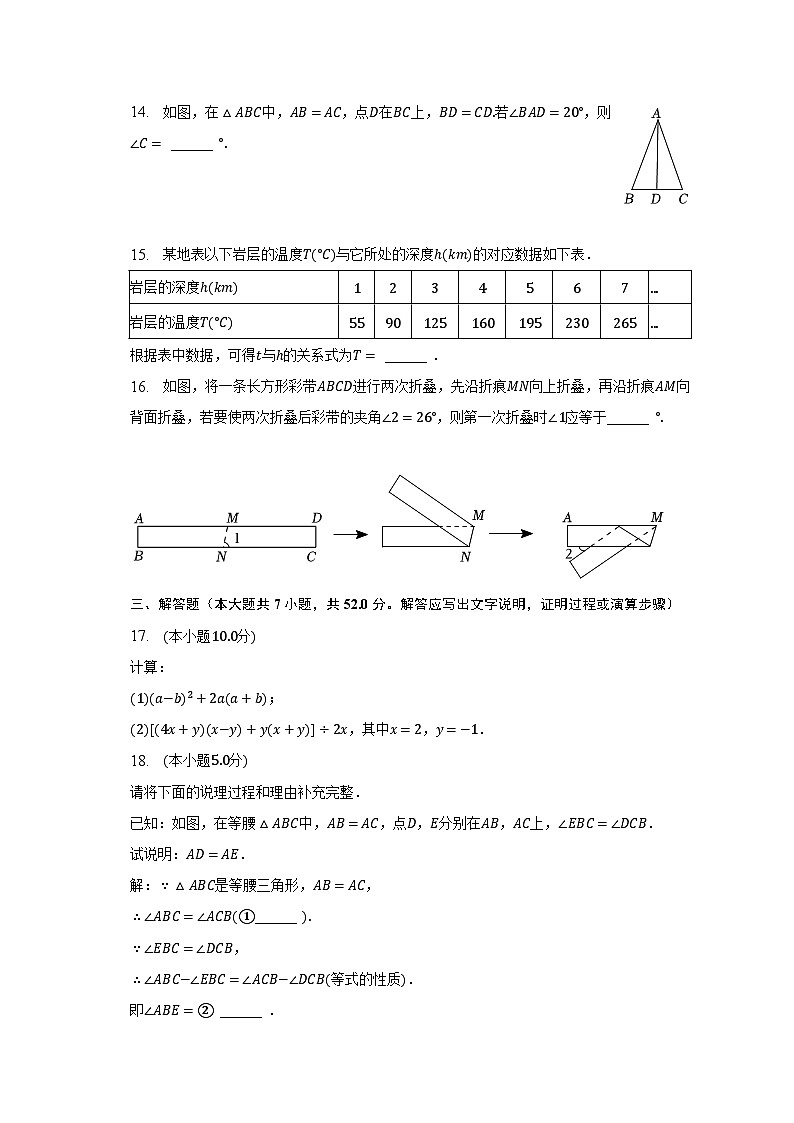
14. 如图，在△ABC中，AB=AC，点D在BC上，BD=CD.若∠BAD=20°，则∠C= ______ °.


15. 某地表以下岩层的温度T(°C)与它所处的深度h(km)的对应数据如下表．
岩层的深度h(km)
1
2
3
4
5
6
7
...
岩层的温度T(°C)
55
90
125
160
195
230
265
...
根据表中数据，可得t与h的关系式为T= ______ ．
16. 如图，将一条长方形彩带ABCD进行两次折叠，先沿折痕MN向上折叠，再沿折痕AM向背面折叠，若要使两次折叠后彩带的夹角∠2=26°，则第一次折叠时∠1应等于______ °.


三、解答题（本大题共7小题，共52.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题10.0分)
计算：
(1)(a−b)2+2a(a+b)；
(2)[(4x+y)(x−y)+y(x+y)]÷2x，其中x=2，y=−1．
18. (本小题5.0分)
请将下面的说理过程和理由补充完整．
已知：如图，在等腰△ABC中，AB=AC，点D，E分别在AB，AC上，∠EBC=∠DCB．
试说明：AD=AE．
解：∵△ABC是等腰三角形，AB=AC，
∴∠ABC=∠ACB(①______ ).
∵∠EBC=∠DCB，
∴∠ABC−∠EBC=∠ACB−∠DCB(等式的性质)．
即∠ABE=② ______ ．
在△ABE和△ACD中，
∵③ ______ ，
AB=AC,∠ABE=∠ACD,
∴△ABE≌△ACD(④______ ).
∴AE=AD( ⑤______ ).

19. (本小题6.0分)
适当强度的运动有益身体健康.小明为了保持身体健康，坚持每天适当运动.某次运动中，小明的心率P与运动时间t之间的变化关系如图所示.根据图象回答问题：
(1)在这个变化过程中，自变量是______ ，因变量是______ ；
(2)图中点M表示的实际意义是什么？
(3)小明通过查阅资料了解到：对于青少年，心率控制在120次/分～175次/分之间能达到最佳的运动效果.问：本次运动中达到最佳运动效果的时间约持续多久？

20. (本小题6.0分)
“击鼓传花”是我国民间的一种传统游戏.如图，8个人围成一圈玩“击鼓传花”游戏，击鼓人背对着大家蒙眼击鼓.鼓响时，“花”在8个人手中依次传递；鼓停时，“花”传到谁手中，谁将上台表演.若不考虑其他因素，在每轮游戏中，可以认为“花”传到每个人手上的可能性相同．
(1)在一轮游戏中，“花”传到偶数位的概率是______ ；
(2)某轮游戏中，“花”从2号位传出，求鼓停时“花”恰好传到与他相邻位置的概率．

21. (本小题7.0分)
如图，已知∠BAC=90°，点D在线段BC上，DE//AC，DE与AB交于点O，∠E+∠B=90°．
(1)试说明：AE//BC；
(2)已知DE=BD，利用尺规作图，在线段AB上作一点P，使得△PDE与△PBD的面积相等.(保留作图痕迹，不写作法)

22. (本小题9.0分)
“九章兴趣小组”开展研究性学习，对两位数乘法的速算技巧进行研究.(友情提示：如果两个正整数和为10，则称这两个数互补.)
小明发现“十位相同，个位互补”的两个两位数相乘有速算技巧．
例如：24×26=100×(2×3)+4×6，结果为624；
42×48=100×(4×5)+2×8，结果为2016；
小红发现“十位互补，个位为5”的两个两位数相乘也有速算技巧．
例如：45×65=100×(4×6+5)+25，结果为2925；
35×75=100×(3×7+5)+25，结果为2625；
(1)请你按照小明发现的技巧，写出计算63×67的速算过程；
(2)请你用含有字母的等式表示小明所发现的速算规律，并验证其正确性；
(3)小颖发现：小红的速算技巧可以推广到“十位互补，个位相同”的两个两位数相乘.请你直接用含有字母的等式表示该规律．
23. (本小题9.0分)
如图，已知△ABC，AB=AC，点E是线段AB上的一个动点，CE的垂直平分线交AC于点M，交CE于点O，交BC于点N．
(1)当∠A=80°，∠BCE=20°时，求∠ACE的度数；
(2)当CE平分∠ACB时，试说明△EOM≌△CON；
(3)探究：在点E的运动过程中，∠AEM与∠BCE有怎样的数量关系？试说明理由．


答案和解析

1.【答案】C 
【解析】解：A，B，D中的图不是轴对称图形，故不符合题意；
C中的图是轴对称图形，故符合题意．
故选：C．
根据轴对称图形的定义逐项识别即可，一个图形的一部分，以某条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做轴对称图形．据此解答即可．
本题考查了轴对称图形的识别，熟练掌握轴对称图形的定义是解答本题的关键．

2.【答案】C 
【解析】解：0.000032=3.2×10−5．
故选：C．
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|