

2022-2023学年山东省德州市临邑县七年级(下)期末数学试卷(含解析)
展开1. 如图,直线a,b被直线c所截,且a//b,则∠1与∠2的位置关系是( )
A. 同位角
B. 对顶角
C. 同旁内角
D. 内错角
2. 在 2,38,0, 9,34,x2,0.3333…… 5,3.1415,2.010101……(相邻两个1之间1个0)中,无理数有( )
A. 2个B. 3个C. 4个D. 5个
3. 把不等式x−4≤3x的解集在数轴上表示出来,则正确的是( )
A. B.
C. D.
4. 如图,在平面直角坐标系xOy中,将四边形ABCD先向上平移,再向左平移得到四边形A1B1C1D1,已知A1(−3,5),B1(−4,3),A(3,3),则点B坐标为( )
A. (1,2)B. (2,1)C. (1,4)D. (4,1)
5. 已知点P(a,b),ab>0,a+b<0,则点P在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
6. 有一个数轴转换器,原理如图所示,则当输入的x为64时,输出的y是( )
A. 8B. 8C. 12D. 18
7. 平面镜在光学仪器中有广泛的应用.平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①.一束光线m射到平面镜a上,被a反射后的光线为n,则∠1=∠2.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=30°时,∠DCN的度数为( )
A. 40°B. 50°C. 60°D. 70°
8. 已知关于x,y的方程组x+5y=4−ax−y=3a.给出下列结论.其中错误的个数是( )
①当a=1时,方程组的解也是方程x+y=4−a的解;
②当a=−2时,x、y的值互为相反数;
③不论a取什么数,2x+7y的值始终不变;
④若x≤1,则y>47.
A. 1个B. 2个C. 3个D. 4个
9. 我国明代数学家程大位所著《算法统宗》中记载了一道有趣的题目:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”题目大意是:100个和尚分100个馒头,刚好分完.大和尚1人分3个馒头,小和尚3人分一个馒头.问大、小和尚各有多少人?若大和尚有x人,小和尚有y人.则下列方程或方程组中:
①x+y=10013x+3y=100;②x+y=1003x+13y=100;③3x+13(100−x)=100;④13(100−y)+3y=100
正确的是( )
A. ①③B. ①④C. ②③D. ②④
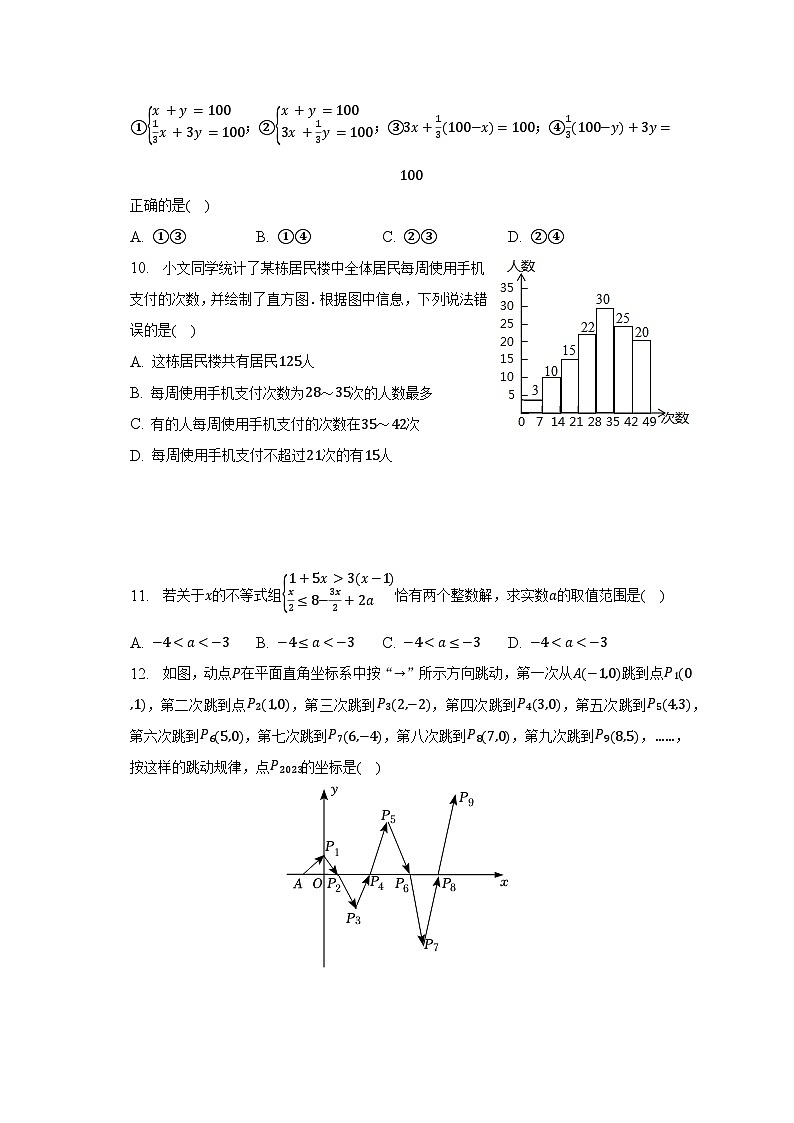
10. 小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
A. 这栋居民楼共有居民125人
B. 每周使用手机支付次数为28~35次的人数最多
C. 有的人每周使用手机支付的次数在35~42次
D. 每周使用手机支付不超过21次的有15人
11. 若关于x的不等式组1+5x>3(x−1)x2≤8−3x2+2a恰有两个整数解,求实数a的取值范围是( )
A. −4
A. (2022,1011)B. (2022,1012)C. (2022,−1011)D. (2022,−1012)
二、填空题(本大题共6小题,共24.0分)
13. −27的立方根是______, 81的平方根是______.
14. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(−2,2),(−3,0),则叶杆“底部”点C的坐标为______ .
15. 我国古代对于利用二元一次方程组解决实际问题早有研究,《九章算术》中记载:“今有上禾三秉.益实六斗,当下禾十秉,下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?“其大意是:今有上等稻子三捆,若打出来的谷予再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆.若打出来的谷子再加一斗,则相当于两捆上等稻子打出来的谷子.问上等.下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子.根据题意可列方程组为______.
16. 已知不等式x+a>12x+b<2的解集为−2
18. 在平面直角坐标系xOy中,将A(a,b),B(m,b+1)(a≠m+1)两点同时向右平移h(h>0)个单位,再向下平移1个单位得到C,D两点(点A对应点C).连接AD,过点B作AD的垂线l,E是直线l上一点,连接DE,且DE的最小值为1.下列结论正确的有______ .(只填序号)
①AC=BD;
②直线l⊥x轴;
③A、B、C三点可能在同一条直线上;
④当DE取最小值时,点E的坐标为(m,b).
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题12.0分)
(1) 25+3−64−|1− 2|;
(2)已知方程组:3x+5y=k+32x+3y=k的解x,y的值之和等于4,求k的值;
(3)解不等式组2x−1≤−x+1x−16
如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为______,∠BOE的邻补角为______;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
21. (本小题10.0分)
△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标:A′____;B′____;C′____;
(2)说明△A′B′C′由△ABC经过怎样的平移得到?____.
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为____;
(4)求△ABC的面积.
22. (本小题10.0分)
请阅读下面材料,并完成相应的任务.
设a、b是有理数,且满足a+ 2b=3−2 2,求ba的值.
解:由题意,得(a−3)+ 2(b+2)=0.
∵a,b都是有理数,
∴a−3,b+2也是有理数.
∵ 2是无理数,
∴b+2=0,a−3=0,即a=3,b=−2.
∴ba=(−2)3=−8.
根据阅读材料,解决问题:
设x,y都是有理数,且满足x2−2y+ 5y=10+3 5,求x+y的值.
23. (本小题12.0分)
如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD//CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
24. (本小题12.0分)
地球上的淡水资源是有限的,为节约用水,某公司准备购进A型和B型两种设备共10台,用于将雨水和生产用水再次收集与重复循环使用.已知购进A型设备3台、B型设备1台,共需97万元;购进A型设备2台、B型设备3台,共需116万元.
(1)购买A型设备和B型设备每台各需多少万元?
(2)已知A型和B型设备每台每天处理的循环水量分别为35吨和30吨,若该公司购买A型和B型两种设备的总费用不超过240万元,为确保这10台设备每天处理的循环水量不少于320吨,则该公司有几种购买方案?
25. (本小题14.0分)
如图1,已知直线MN//直线PQ,点A为直线MN上一点,点B为直线PQ上一点,且∠ABP=8O°,点C是直线PQ上一动点,且点C在点B右侧,过点C作CD//AB交直线MN于点D,连接AC.
(1)若AC平分∠BAD,请直接写出∠ACD的度数;
(2)作∠CAE=∠CAD,交直线PQ于点E,AF平分∠BAE.(说明:解答过程用数字表示角)
①如图2,若点E,F都在点B的右侧,求∠CAF的度数.
②在点C的运动过程中,是否存在这样的情形,使∠AFB=3∠EAF成立?若存在,求出∠ACD的度数:若不存在,请说明理由.
答案和解析
1.【答案】A
【解析】解:∵直线a,b被直线c所截,
∴∠1与∠2的位置关系是同位角.
故选:A.
根据对顶角、同位角、内错角、同旁内角的定义判断即可.
本题考查了平行线的性质和同位角,熟练掌握同位角的定义是解题关键.
2.【答案】B
【解析】解:38=2, 9=3,
故在 2,38,0, 9,34,x2,0.3333…… 5,3.1415,2.010101……(相邻两个1之间1个0)中,无理数有 2,34, 5,共3个.
故选:B.
根据无理数的定义进行解答即可.
本题考查的是无理数,熟知无限不循环小数叫做无理数是解题的关键.
3.【答案】B
【解析】解:x−4≤3x,
移项得x−3x≤4,
合并同类项得−2x≤4,
把未知数系数化为1得x≥−2,
表示在数轴上如下:
故选:B.
根据解一元一次不等式的步骤求出不等式的解集,再表示在数轴上即可.
本题考查解一元一次不等式,解题的关键是掌握解一元一次不等式的一般步骤.
4.【答案】B
【解析】解:由题意A1(−3,5)向右平移6个单位,再向下平移2个单位得到A(3,3),
∴B1(−4,3)向右平移6个单位,再向下平移2个单位得到B(2,1),
故选:B.
利用平移规律解决问题即可.
本题考查坐标与图形变化−平移,解题的关键是掌握平移变换的性质,属于中考常考题型.
5.【答案】C
【解析】解:∵ab>0,
∴a,b同号,
∵a+b<0,
∴a<0,b<0,
故P点在第三象限.
故选:C.
根据条件可得:a<0,b<0,进而即可判断点P所在的象限.
本题主要考查平面直角坐标系中,各个象限的点的坐标特征,掌握各个象限的点的坐标特征,是解题的关键.
6.【答案】B
【解析】解:64的算术平方根是8,
8的算术平方根是 8.
故选:B.
根据算术平方根,即可解答.
本题考查了算术平方根,解决本题的根据是熟记算术平方根的定义.
7.【答案】C
【解析】解:由题意得∠ABM=∠CBO,∠BCO=∠DCN,
∵∠ABM=30°,
∴∠CBO=30°,
∴∠ABC=180°−∠ABM−∠CBO=180°−30°−30°=120°,
∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=60°,
∵∠BCD+∠BCO+∠DCN=180°,
∴∠DCN=60°,
故选:C.
由题意得∠ABM=∠CBO,∠BCO=∠DCN,根据平角的定义可求出∠ABC的度数,再根据两直线平行,同旁内角互补求出∠BCD的度数,从而求出∠DCN
的度数.
本题考查了平行线的性质,平面镜反射光线的规律,熟练掌握两直线平行,同旁内角互补是解题的关键.
8.【答案】B
【解析】解:解方程组得x=2+7a3y=2−2a3,
①当a=1时,则x=3y=0,代入方程x+y=3,左边=右边,故正确,不符合题意;
②当a=−2时,则x=−4y=2,x、y不是互为相反数,故错误,符合题意;
③因为2x+7y=4+14a3+14−14a3=6,所以不论a取什么数,2x+7y的值始终不变,故正确,不符合题意;
④若x≤1,则2+7a3≤1,解得a≤17,此时2−2a3≥47,故错误,符合题意;
故选:B.
解方程组得x=2+7a3y=2−2a3,①将a=1的值代入方程组的解和方程中进行判断即可;②将a=−2代入方程组的解,依据相反数的概念判断即可;③将所求x、y代入2x+7y,判断最后化简结果与a有无关系即可;④由x≤1得出a的范围,再结合a的范围求出2−2a3的范围即可.
本题主要考查解二元一次方程组和一元一次不等式组,解题的关键是掌握解二元一次方程组和一元一次不等式及不等式组的能力.
9.【答案】C
【解析】解:设大和尚有x人,小和尚有y人,
依题意,得:x+y=1003x+13y=100,
∴y=100−x,
∴3x+13(100−x)=100.
∴②③正确.
故选:C.
设大和尚有x人,小和尚有y人,根据100个和尚分100个馒头且大和尚1人分3个馒头、小和尚3人分一个馒头,即可得出关于x,y的二元一次方程组,变形后可得出3x+13(100−x)=100,此题得解.
本题考查了由实际问题抽象出二元一次方程组以及由实际问题抽象出一元一次方程,找准等量关系,正确列出二元一次方程组(或一元一次方程)是解题的关键.
10.【答案】D
【解析】解:A、这栋居民楼共有居民3+10+15+22+30+25+20=125(人),此结论正确;
B、每周使用手机支付次数为28~35次的人数最多,此结论正确;
C、有的人每周使用手机支付的次数在35~42次,此结论正确;
D.每周使用手机支付不超过21次的有3+10+15=28人,此结论错误;
故选:D.
根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.【答案】B
【解析】解:解不等式1+5x>3(x−1),得:x>−2,
解不等式x2≤8−3x2+2a,得:x≤4+a,
则不等式组的解集为−2
∴不等式组的整数解为−1、0,
则0≤4+a<1,
解得−4≤a<−3,
故选:B.
先解不等式组求得−2
12.【答案】D
【解析】解:观察图象,结合动点P第一次从A(−1,0)跳到点P1(0,1),第二次运动到点P2(1,0),第三次运动到P3(2,−2),第四次运动到P4(3,0),第五运动到P5(4,3),第六次运动到P6(5,0),第七次跳到P7(6,−4),第八次跳到P8(7,0),第九次跳到P9(8,5),…,
横坐标为:0,1,2,3,4,5,6,…,
纵坐标为:1,0,−2,0,3,0,−4,0,5,0,−6,…,
可知Pn的横坐标为n−1,当n为偶数时纵坐标为0,当n为奇数时,纵坐标为±n+12,当n+12为偶数时符号为负,当n+12奇数时符号为正,
∴P2023的横坐标为2021,纵坐标为−1012.
故选:D.
观察图象,结合动点P的横坐标和纵坐标可得规律即可.
本题考查了规律型点的坐标,数形结合并从图象中发现循环规律是解题的关键.
13.【答案】−3 ±3
【解析】解:−3的立方为−27,故−27的立方根为−3,
81=9,故9的平方根为±3,
故答案为−3、±3.
根据平方根和立方根的知识点进行解答,若x3=a,则x=3a,x2=b(b≥0)则x=± b,据此得到答案.
本题主要考查立方根和平方根的知识点,基础题,比较简单,但注意个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.立方根的性质:一个正数的立方根式正数,一个负数的立方根是负数,0的立方根式0.
14.【答案】(2,−3)
【解析】解:因为A,B两点的坐标分别为(−2,2),(−3,0),
所以得出坐标轴如下图所示位置:
所以点C的坐标为(2,−3).
故答案为:(2,−3).
根据A,B的坐标确定出坐标轴的位置,点C的坐标可得.
本题主要考查了用坐标确定位置,和由点的位置得到点的坐标.依据已知点的坐标确定出坐标轴的位置是解题的关键.
15.【答案】3x+6=10y5y+1=2x
【解析】解:设上等稻子每捆打x斗谷子,下等稻子每捆打y斗谷子,
根据题意可列方程组为:3x+6=10y5y+1=2x.
故答案为:3x+6=10y5y+1=2x.
设上等稻子每捆打x斗谷子,下等稻子每捆打y斗谷子,分别利用已知“今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子;有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打出来的谷子”分别得出等量关系求出答案.
此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
16.【答案】−1
【解析】解:由x+a>1,得:x>1−a,
由2x+b<2,得:x<2−b2,
∵不等式组的解集为−2
解得a=3,b=−4,
∴(a+b)2023
=(3−4)2023
=(−1)2023
=−1,
故答案为:−1.
分别求出每一个不等式的解集,根据不等式组的解集得出a、b的值,再代入计算即可.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
17.【答案】(12n+30)
【解析】
【分析】
此题考查了平行线的性质,用到的知识点是翻折变换的性质;注意数形结合思想的应用.根据折叠得到∠AEB=∠1=60°,然后求得∠AED′的度数,再根据∠AED=n°,即可求得∠DED′的度数,继而求得∠BCE的度数.
【解答】
解:如图,
∵∠ABE=30°,∠A=90°,
∴∠1=60°,
∵折叠
∴∠AEB=∠1=60°,
∴∠AED′=180°−∠1−∠AEB=180°−60°−60°=60°,
∴∠DED′=∠AED+∠AED′=n°+60°=(n+60)°,
∴∠2=12∠DED′=(12n+30)°,
∵A′D′//BC,
∴∠BCE=∠2=(12n+30)°.
故答案为(12n+30).
18.【答案】①②④
【解析】解:如图,直线l交AD于点P,
∵A(a,b),B (m,b+1)(a≠m+1)两点同时向右平移h(h>0)个单位,再向下平移1个单位得到C,D两点(点A对应点C),
一个点向右平移h个单位,则该点的横坐标加h;一个点向下平移1个单位,则该点的纵坐标减1,
∴C(a+h,b−1),D(m+h,b),
∵此时点A和点D的纵坐标相同,
∴AD//x轴.
根据平移的性质可知:AC=BD,故①正确;
∵AD//x轴,1⊥AD,
∴直线l⊥x轴,故②正确;
由图可知:因为a≠m+1,所以A、B、C三点不可能在同一条直线上,故③错误;
当DE取最小值时,点E与点P重合时,
此时点E的坐标为(m,b),故④正确,
故答案为:①②④.
根据平移的性质先求出点C和点D的坐标,得到点A和点D的纵坐标相同,进而得到AD//x轴,再利用平移的性质来求解.
此题主要考查了平移的性质,理解平移的性质和求出点C和点D的坐标是解题的关键.
19.【答案】解:(1) 25+3−64−|1− 2|
=5+(−4)−( 2−1)
=5−4− 2+1
=2− 2;
(2)3x+5y=k+32x+3y=k,
解得:x=2k−9y=6−k,
∵x+y=4,
∴2k−9+6−k=4,
解得:k=7,
∴k的值为7;
(3)2x−1≤−x+1①x−16
解不等式②得:x>−1,
∴原不等式组的解集为:−1
【解析】(1)先化简各式,然后再进行计算即可解答;
(2)先解方程组可得:x=2k−9y=6−k,然后根据题意可得x+y=4,从而可得2k−9+6−k=4,最后进行计算即可解答;
(3)按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了解一元一次不等式组,二元一次方程组的解,实数的运算,在数轴上表示不等式的解集,准确熟练地进行计算是解题的关键.
20.【答案】解:(1)∠BOD; ∠AOE ;
(2)∵∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD及∠BOE:∠EOD=2:3,
∴得∠EOD=32∠BOE,
∴∠BOE+32∠BOE=70°,
∴∠BOE=28°,
∴∠AOE=180°−∠BOE=152°.
【解析】解:(1)∠AOC的对顶角为∠BOD,∠BOE的邻补角为∠AOE;
故答案为:∠BOD; ∠AOE ;
(2)∵∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD及∠BOE:∠EOD=2:3,
∴得∠EOD=32∠BOE,
∴∠BOE+32∠BOE=70°,
∴∠BOE=28°,
∴∠AOE=180°−∠BOE=152°.
(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
本题主要考查了对顶角,邻补角的定义,利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解.
21.【答案】 解:(1)A′(−3,1); B′(−2,−2);C′(−1,−1);
(2)先向左平移4个单位,再向下平移2个单位;
或:先向下平移2个单位,再向左平移4个单位;
(3)P′(a−4,b−2);
(4)△ABC的面积=2×3−12×1×3−12×1×1−12×2×2
=6−1.5−0.5−2
=2.
【解析】解:(1)根据题意可知:A′(−3,1); B′(−2,−2);C′(−1,−1);
(2)根据图形可知:先向左平移4个单位,再向下平移2个单位;
或:先向下平移2个单位,再向左平移4个单位;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为:(a−4,b−2).
故答案为:(a−4,b−2);
(4)△ABC的面积=2×3−12×1×3−12×1×1−12×2×2,
=6−1.5−0.5−2,
=2.
(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据对应点A、A′的变化写出平移方法即可;
(3)根据平移规律逆向写出点P′的坐标;
(4)利用△ABC所在的长方形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
本题考查了利用平移变换作图,熟练掌握网格结构,根据对应点的坐标确定出平移的方法是解题的关键.
22.【答案】解:∵x2−2y+ 5y=10+3 5,
∴(x2−2y−10)+( 5y−3 5)=0,
∴(x2−2y−10)+ 5(y−3)=0,
∵x,y都是有理数,
∴x2−2y−10,y−3也是有理数,
∵ 5是无理数,
∴x2−2y−10=0,y−3=0,
解得:y=3,x=±4,
当x=4,y=3时,x+y=7;
当x=−4,y=3时,x+y=−1;
综上所述:x+y的值为7或−1.
【解析】根据例题的解题思路进行计算,即可解答.
本题考查了实数的运算,理解例题的解题思路是解题的关键.
23.【答案】(1)证明:∵∠1=∠BDC,
∴AB//CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD//CE;
(2)解:∵CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD//CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF−∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
【解析】(1)根据同位角相等,两直线平行可判定AB//CD,得到∠2=∠ADC,等量代换得出∠ADC+∠3=180°,即可根据同旁内角互补,两直线平行得解;
(2)由CE⊥AE,AD//CE得出∠DAF=∠CEF=90°,再根据平行线的性质即可求出∠ADC=∠2=35°,再根据角平分线的定义即可得解.
此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的基础.
24.【答案】解:(1)设A型设备每台需x万元,B型设备每台需y万元,
根据题意得3x+y=972x+3y=116,
解得x=25y=22,
答:A型设备每台需25万元,B型设备每台需22万元;
(2)设购买A型设备m台,则购买B型设备(10−m)台,
根据题意,得25m+22(10−m)≤24035m+30(10−m)≥320,
解得4≤m≤203,
∵m只能取正整数,
∴m=4或5或6,
∴该公司有三种购买方案;
∵A型设备的单价比B型设备的单价贵,
∴购买A型设备4台,B型设备6台,
购买A型设备5台,B型设备5台,
购买A型设备6台,B型设备4台.
【解析】(1)设A型设备每台需x万元,B型设备每台需y万元,根据“购进A型设备3台、B型设备1台,共需97万元;购进A型设备2台、B型设备3台,共需116万元”列二元一次方程组,从而可以解答本题;
(2)设购买A型设备m台,则购买B型设备(10−m)台,根据“该公司购买A型和B型两种设备的总费用不超过240万元,为确保这10台设备每天处理的循环水量不少于320吨”列不等式组求出m的取值范围,再根据两种设备的单价解答即可.
本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答.
25.【答案】解:(1)∵MN//PQ,∠ABP=80°,
∴∠BAD=∠ABP=80°,
∵AC平分∠BAD,
∴∠BAC=40°,
∵CD//AB,
∴∠ACD=∠BAC=40°;
(2)①∵AF平分∠BAE,
∴∠EAF=12∠BAE,
∵∠CAE=∠CAD,
∴∠CAF=12∠BAD=40°;
②存在.
当∠BAF=∠EAF=∠CAE=∠CAD时,
∠AFB=∠DAF=3∠EAF,
∵∠ABP=∠DAB=80°,
∴∠BAF=∠EAF=∠CAE=∠CAD=20°,
∴∠BAC=60°,
∵CD//AB,
∴∠ACD=∠BAC=60°.
【解析】(1)先根据平行线的性质求得∠BAD,再根据角平分线的定义求得结果;
(2)①根据平行线的性质与折叠性质,角平分线的定义求解便可;
②根据平行线的性质,角的大小关系便可解答.
本题考查了平行线的性质,角平分线的定义,关键是正确应用角平分线定义与平行线的性质解题.
2023-2024学年山东省德州市临邑县七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年山东省德州市临邑县七年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省德州市临邑县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省德州市临邑县八年级(下)期末数学试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省德州市临邑县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省德州市临邑县八年级(下)期末数学试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












