九上数学华东师大第24章单元测试卷

这是一份九上数学华东师大第24章单元测试卷，共12页。

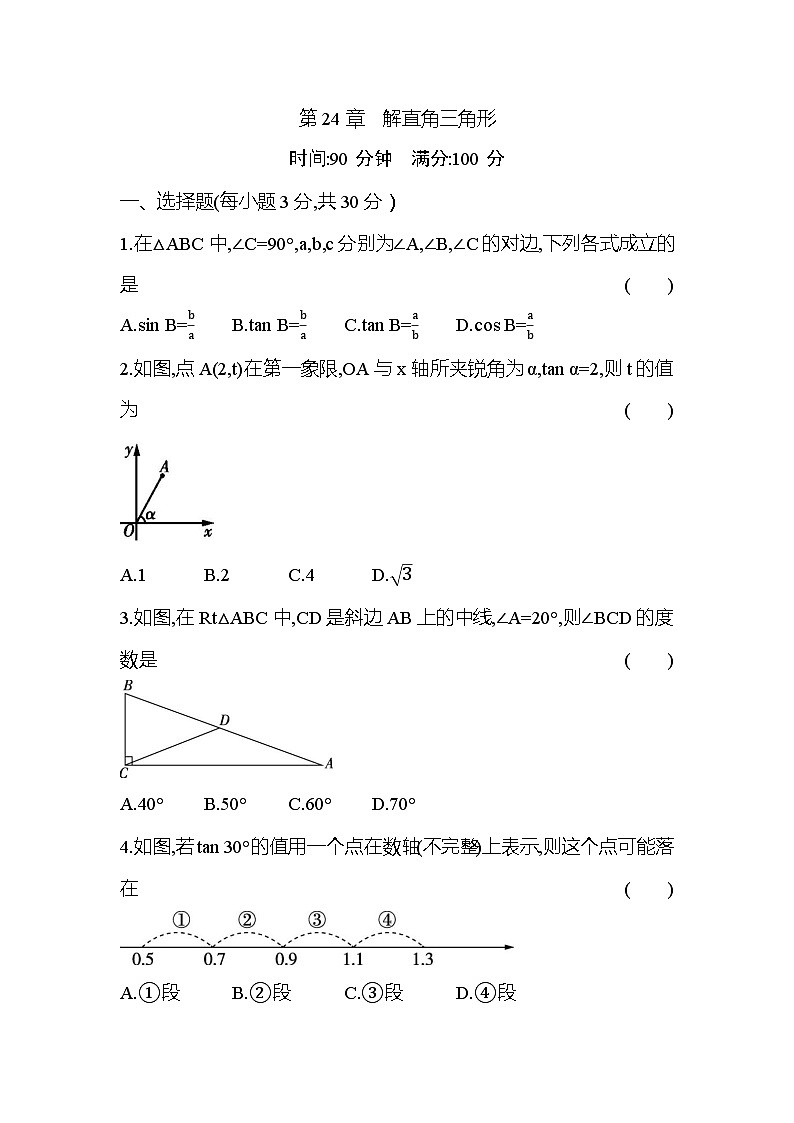
第24章　解直角三角形
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分）　　　 　　　　　　　　　　
1.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列各式成立的是(　　)
A.sin B=ba B.tan B=ba C.tan B=ab D.cos B=ab
2.如图,点A(2,t)在第一象限,OA与x轴所夹锐角为α,tan α=2,则t的值为(　　)

A.1　　 B.2　　 C.4　　 D.3
3.如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD的度数是(　　)

A.40° B.50° C.60° D.70°
4.如图,若tan 30°的值用一个点在数轴(不完整)上表示,则这个点可能落在(　　)

A.①段 B.②段 C.③段 D.④段
5.Rt△ABC中,∠C=90°,AC=15,AB边上的中线CD=172,则sin A为(　　)
A.817　　 B.217　　 C.1517　　　 D.815
6.如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为(　　)

A.23 B.43 C.22 D.223
7.如图,工人师傅将截面为矩形的木条锯成两部分,四边形ABCD和四边形AEFG都是矩形,点C,B,G在同一直线上,CB=a,BG=b,∠AGB=β,则点E到CG的距离等于(　　)

A.acos β+bsin β B.acos β+btan β
C.asin β+btan β D.bsin β+atan β
8.如图,在Rt△ABC中,∠C=90°,AB=5 cm,tan B=34,点D从点A出发沿AC方向以1 cm/s的速度向点C运动.过点D作DE∥AB交BC边于点E,过点E作EF⊥BC交AB边于点F,当四边形ADEF为菱形时,点D运动的时间为(　　)

A.32 s B.52 s C.127 s D.158 s
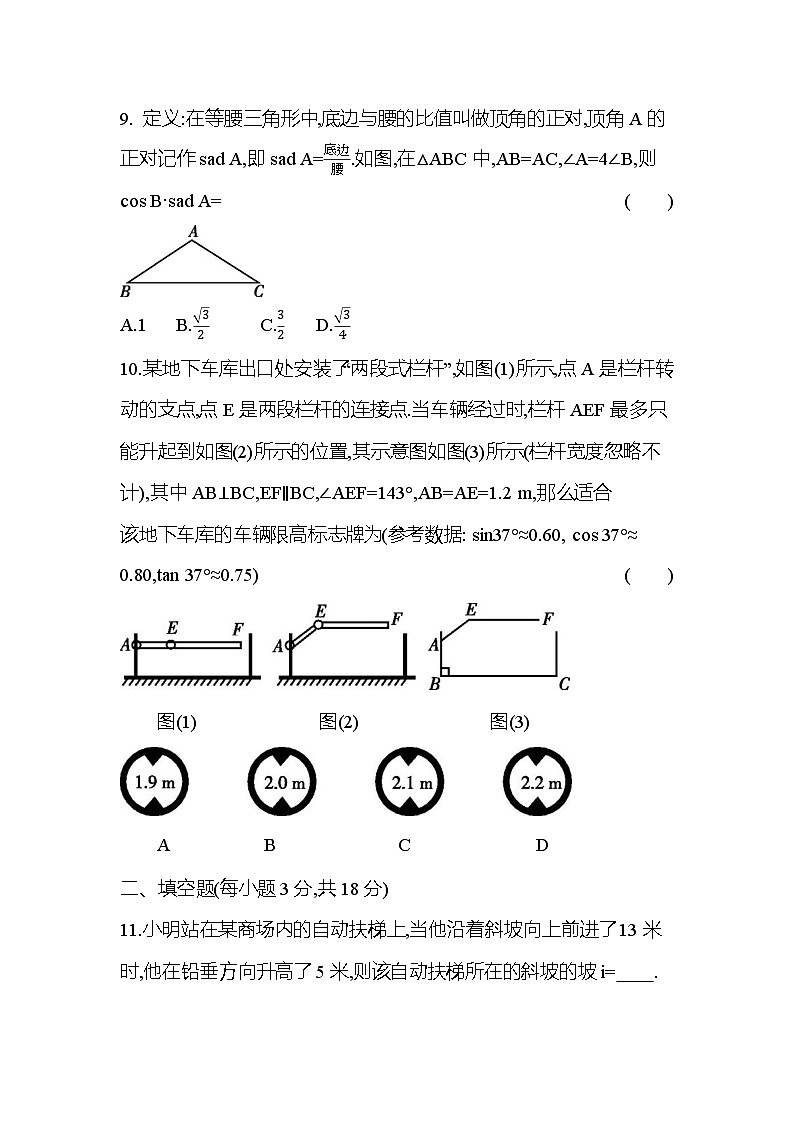
9. 定义:在等腰三角形中,底边与腰的比值叫做顶角的正对,顶角A的正对记作sad A,即sad A=底边腰.如图,在△ABC中,AB=AC,∠A=4∠B,则cos B·sad A=(　　)

A.1 B.32 C.32 D.34
10.某地下车库出口处安装了“两段式栏杆”,如图(1)所示,点A是栏杆转动的支点,点E是两段栏杆的连接点.当车辆经过时,栏杆AEF最多只能升起到如图(2)所示的位置,其示意图如图(3)所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2 m,那么适合
该地下车库的车辆限高标志牌为(参考数据: sin37°≈0.60, cos 37°≈
0.80,tan 37°≈0.75)(　　)

　 图(1)　　 　　图(2)　 　　图(3)

A　 　 B　 C　 　 　D
二、填空题(每小题3分,共18分)
11.小明站在某商场内的自动扶梯上,当他沿着斜坡向上前进了13米时,他在铅垂方向升高了5米,则该自动扶梯所在的斜坡的坡i=　　. 
12.已知△ABC中,∠C=90°,sin A=45,BC=20,则△ABC的周为　　　. 
13.在△ABC中,∠A为锐角,(2sin A-1)2+22-cosB=0,若AB=10,则BC=　　　. 
14.在△ABC中,tan B=34,BC边上的高AD=6,AC=35,则BC边的长等于　　　. 
15.对于任意锐角α,β,有等式sin(α+β)=sin αcos β+cos αsin β.结合所学知识,利用上述公式可以求得sin 75°的值是　　　　　. (结果保留根号)
16.如图,一艘船由A港沿北偏东65°方向航行302 km至B港,再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向上,则A,C两港之间的距离为　　　　km. 

三、解答题(共52分)
17.(每小题3分,共6分)计算:
(1)3sin 30°·cos 60°-tan230°； (2)tan60°+2sin45°tan45°-cos 30°.



18.(6分)如图,射线OA放置在3×5的正方形网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB,AB,使△AOB为直角三角形,且
(1)使tan∠AOB的值为1; (2)使tan∠AOB的值为12.

图(1)　　　　　　图(2)

19.(8分)如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=2,BD=3.
(1)求sin ∠CBD的值;
(2)若AB=3,求AD的长.








20.(10分)如图,从热气球C处测得两物体A,B的俯角分别为29.5°和45°.如果这时气球的高度CD为80米,且点A,D,B在同一直线上,求物体A,B之间的距离.(结果精确到1米.参考数据:sin 29.5°≈0.49,cos 29.5°≈0.87,tan 29.5°≈0.57)






21.(10分)某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们确定了测量方案,并完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,该小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如表(尚不完整).
课题
测量旗杆的高度
成员
组长:×××　组员:×××,×××,×××
测量工具
测量角度的仪器,皮尺等
测量
示意图

说明:线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.5 m,测点A,B与H在同一条水平直线上,A,B之间的距离可以直接测得,且点G,H,A,
B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上.
测量数据
测量项目
第一次
第二次
平均值
∠GCE的度数
26.4°
26.6°
26.5°
∠GDE的度数
32.7°
33.3°
33°
A,B之间的距离
5.9 m
6.1 m

…
…
任务一:两次测量A,B之间的距离的平均值是　　　　m. 
任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(参考数据:sin 26.5°≈0.45,cos 26.5°≈0.89,tan 26.5°≈0.50,sin 33°≈0.54,cos 33°≈
0.84,tan 33°≈0.65)
任务三:该“综合与实践”小组在确定方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)



22.(12分)在△ABC中,∠ABC=90°.
(1)如图(1),分别过A,C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图(2),P是边BC上一点,∠BAP=∠C,tan∠PAC=255,求tan C的值;
(3)如图(3),D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=35,ADAC=25,求tan∠CEB的值.

图(1) 图(2) 图(3)













参考答案与解析
第24章　解直角三角形
1.B　
2.C
3.D　
4.A
5.A　6.C　
7.B　
8.D　
9.C　
10.A　
11.1∶2.4　12.60　13.52　
14.5或11 　15.6+24　
16.(30+103)　
17.解：(1)原式=3×12×12-(33)2=34-13=512.(3分)
(2)原式=3+2×221-32=3+2-32 =32+2.(3分)
18.解：(1)如图(1)所示.(3分)
(2)如图(2)所示.(6分)

　图(1)　　　 图(2)
19.
解：(1)如图,过点D作DE⊥BC于点E.
在Rt△CED中,∵∠C=45°,CD=2,∴CE=DE=1.(2分)
在Rt△BDE中,sin ∠CBD=DEBD=13.(4分)
(2)如图,过点D作DF⊥AB于点F,则∠BFD=∠BED=∠ABC=90°,
∴四边形BEDF是矩形,∴BF=DE=1.(6分)
∵BD=3,∴DF=32-12=22.
∵AF=AB-BF=2,∴AD=(22)2+22=23.(8分)

20.解：(“背靠背”型)由已知得，
∠ECA=29.5°,∠FCB=45°,CD=80米，EF∥AB,CD⊥AB,(2分)
∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,∴BD=CD=80米.(4分)
在Rt△ACD中,∠CDA=90°,tan A=CDAD,∴AD=CDtanA≈800.57≈140(米),(6分)
∴AB=AD+BD=140+80=220(米).(9分)
答:物体A,B之间的距离约为220米.(10分)
21.解：任务一:6(2分)
任务二:设EG=x m,在Rt△DEG中,∠DEG=90°,∠GDE=33°.
∵tan 33°=EGDE,∴DE=xtan33° m.(4分)
在Rt△CEG中,∠CEG=90°,∠GCE=26.5°.
∵tan 26.5°=EGCE,∴CE=xtan26.5° m.(6分)
又∵CD=CE-DE=AB=6 m,∴xtan26.5°-xtan33°=6,解得x≈13.
∴GH=EG+EH=13+1.5=14.5 (m).
答:旗杆GH的高度约为14.5 m.(8分)
任务三:受天气条件影响,没有太阳光线.(答案不唯一,合理即可得分)(10分)
22.解：(1)证明:∵∠M=∠ABC=90°,
∴∠MAB+∠MBA=∠NBC+∠MBA=90°,∴∠MAB=∠NBC.
又∵∠M=∠N=90°,∴△ABM∽△BCN.(3分)
(2)过点P作PM⊥AP,交AC于点M,过点M作MN⊥PC于点N,
如图(1),则△PMN∽△APB,∴PNAB=PMAP=tan∠PAC=255.(5分)
设PN=2t,则AB=5t,
∵∠BAP=∠MPC,∠BAP=∠C,∴∠MPC=∠C,∴CN=PN=2t.
易知△ABP∽△CBA,则ABBC=BPAB,∴AB2=BP·BC,
即(5t)2=BP·(BP+4t),得BP=t(负值已舍去),
∴BC=5t,∴tan C=ABBC=55.(8分)
　　
图(1) 图(2)
(3)过点A作AH⊥EB于点H,过点C作CK⊥EB,交EB的延长线于点K,则△AHB∽△BKC,CK∥AH,如图(2).
∵sin∠BAC=35,∴在Rt△ABC中,AB∶BC∶AC=4∶3∶5,
∴BHCK=ABBC=43,HKEH=ACAD=52.(10分)
∵AE=AB,AH⊥EB,∴EH=BH,∴EK=72BH,∴tan∠CEB=CKEK=CKBH·BHEK=314.(12分)