
初中数学北师大版九年级下册1 圆教案
展开
这是一份初中数学北师大版九年级下册1 圆教案,共4页。教案主要包含了考点梳理,精选例题等内容,欢迎下载使用。
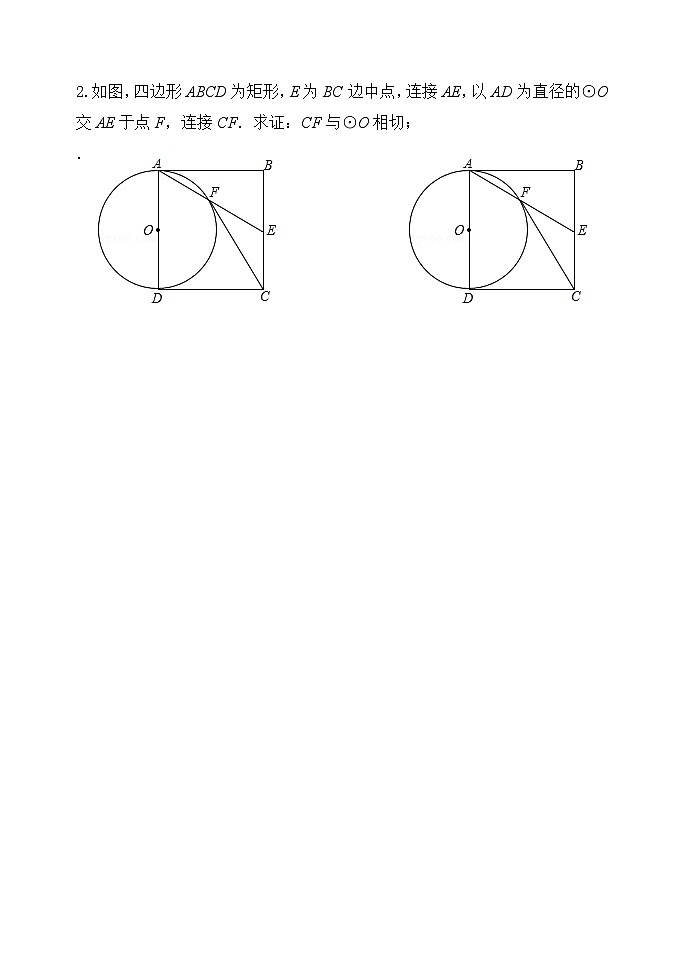
九年级数学第二轮总复习教学案课题:圆切线的性质和判定专题 课型:复习课 学习目标:1.回顾圆的切线的性质定理与判定定理。 2、熟练运用圆的切线的性质与判定定理解决数学问题。教学重点:运用圆的切线的性质与判定定理解决数学问题教学难点:运用圆的判定定理解决数学问题一、考点梳理1、(1)切线的判定定理 (2)切线的性质定理2.主要题型:(1)一是连半径证垂直,(2)二是作垂线证半径二、精选例题1、如图,在△ABC中,∠BCA =90°,以BC为直径的⊙O交AB于点P,点Q是AC的中点.判断直线PQ与⊙O的位置关系,并说明理由. 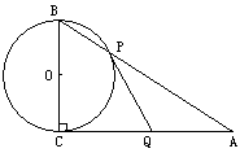 2.如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.求证:CF与⊙O相切;
2.如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.求证:CF与⊙O相切;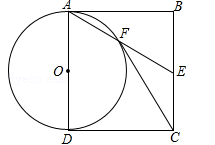
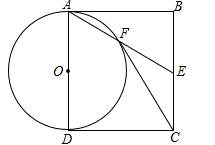 . 3.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
. 3.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.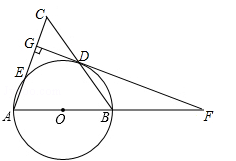 (1)求证:直线FG是⊙O的切线;(2)如图①若AC=10,cosA=
(1)求证:直线FG是⊙O的切线;(2)如图①若AC=10,cosA=![]() ,求CG的长.(3)如图②若AC=10 tan∠BAD =
,求CG的长.(3)如图②若AC=10 tan∠BAD =![]() ,求BF的长.(4) 如图②若BF=5. DF=
,求BF的长.(4) 如图②若BF=5. DF=![]() ,求阴影部分面积图①
,求阴影部分面积图① 图② 三.课后作业1.⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.(1)求证:BE⊥CE;(2)若BC=
图② 三.课后作业1.⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.(1)求证:BE⊥CE;(2)若BC=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求线段CD的长度.
,求线段CD的长度.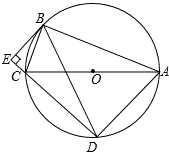 2如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE. (1)求证:DF为⊙O的切线;(2)若AC=3,BC=9,求DE的长.
2如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE. (1)求证:DF为⊙O的切线;(2)若AC=3,BC=9,求DE的长. 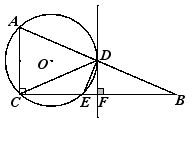
相关教案
这是一份初中数学北师大版九年级下册1 圆教学设计,共2页。
这是一份初中数学北师大版九年级下册第三章 圆7 切线长定理教案设计,共4页。教案主要包含了教材分析,学情分析,教法,教学过程分析,教学评价等内容,欢迎下载使用。
这是一份数学九年级下册1 圆教学设计及反思,共5页。教案主要包含了创设情境,引入新课,师生合作,探究新知,随堂练习,巩固提高,课堂小结,反思提高,巩固新知 ,拓展应用,布置作业,课后促学等内容,欢迎下载使用。










