

四川省达州市渠县清溪中学2022-2023学年八年级下学期期末数学试卷(含答案)
展开四川省达州市渠县清溪中学2022-2023学年八年级下学期期末数学试卷(解析版)
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)历时7年研发建设完成,拥有100%自主知识产权的“云巴”(如图)在重庆璧山正式运行( )
A.对称 B.旋转 C.平移 D.跳跃
2.(4分)分式的值为零,则x等于( )
A.1 B.﹣1 C.0 D.0或1
3.(4分)如图所示,在数轴上表示不等式正确的是( )
A.x<1 B.x≤1 C.x>1 D.x≥1
4.(4分)下列说法错误的是( )
A.若a>b,则a+3>b+3 B.若a>b,则3﹣2a<3﹣2b
C.若ac2<bc2,则a<b D.若a<b,则
5.(4分)如图,在同一平面内,将△ABC绕点A逆时针方向旋转30°到△AB′C′,则∠AC′C等于( )
A.60° B.65° C.70° D.75°
6.(4分)把多项式m(a﹣2)+(a﹣2)分解因式等于( )
A.m(a﹣2) B.(a﹣2)(m+1) C.m(a+2) D.(m﹣1)(a﹣2)
7.(4分)下列命题中是真命题的是( )
A.一组边、一组角对应相等的两个直角三角形全等
B.若等腰三角形的两边长分别为5cm,6cm,则该等腰三角形的周长是16cm
C.平行四边形是中心对称图形,两条对角线的交点是它的对称中心
D.三角形中三边的垂直平分线的交点到三边的距离相等
8.(4分)如图,在平行四边形ABCD中,对角线AC,E是AD的中点,连接OE.若AC=8,则平行四边形ABCD的周长为( )
A.17 B.20 C.26 D.34
9.(4分)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
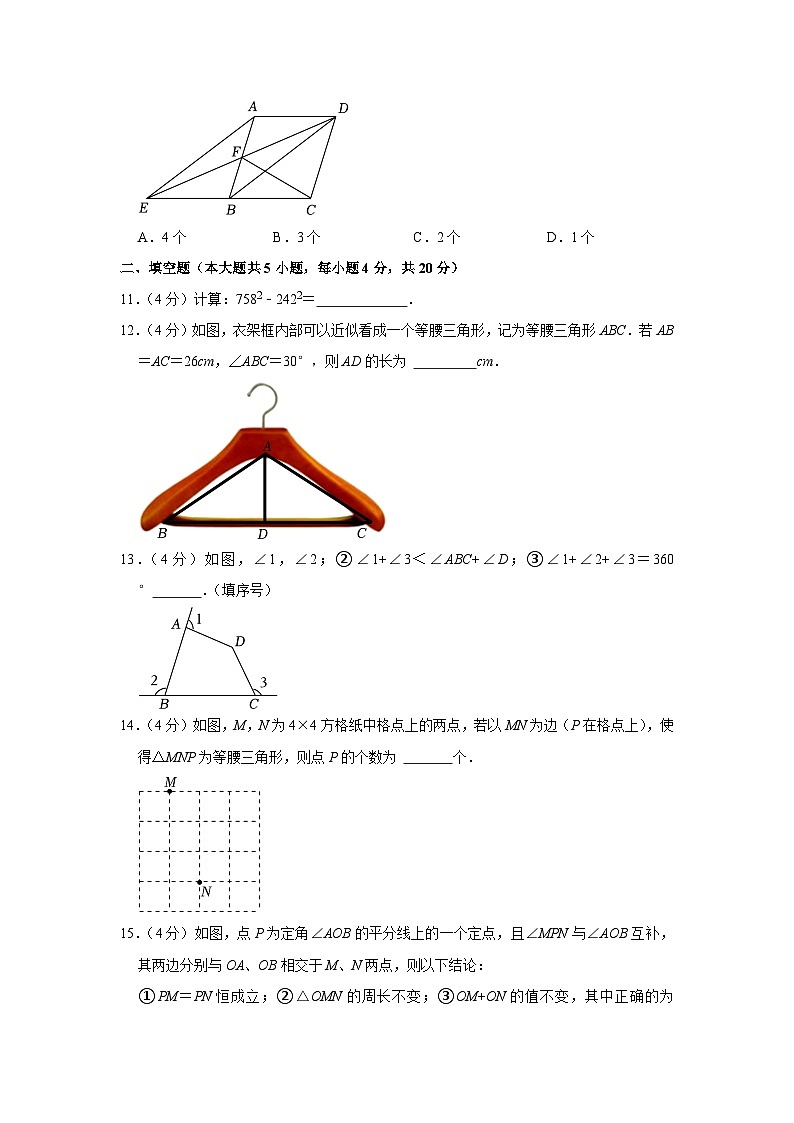
10.(4分)如图,四边形ABCD是平行四边形,AE∥BD,连接DE交AB于点F,连接CFEC:②四边形AEBD是平行四边形:③若∠ADF=∠BCF,则∠ABC=90°,则△DCE是直角三角形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共5小题,每小题4分,共20分)
11.(4分)计算:7582﹣2422= .
12.(4分)如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC.若AB=AC=26cm,∠ABC=30°,则AD的长为 cm.
13.(4分)如图,∠1,∠2;②∠1+∠3<∠ABC+∠D;③∠1+∠2+∠3=360° .(填序号)
14.(4分)如图,M,N为4×4方格纸中格点上的两点,若以MN为边(P在格点上),使得△MNP为等腰三角形,则点P的个数为 个.
15.(4分)如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,其两边分别与OA、OB相交于M、N两点,则以下结论:
①PM=PN恒成立;②△OMN的周长不变;③OM+ON的值不变,其中正确的为 (请填写正确结论前面的序号).
三、解答题(本大题共10小题,共90分)
16.(8分)(1)解分式方程:;
(2)解不等式组,并把解集在数轴上表示出来.
17.(8分)先化简:,再从﹣2.﹣1,0,1中挑一个自己喜欢的整数代入求值.
18.(6分)已知关于x的分式方程=2的解为正数,求m的取值范围.
19.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,△ABC的三个顶点A(5,5),B(6,3),C(2,1)均在格点上.
(1)画出将△ABC向下平移4个单位长度得到的△A1B1C1;
(2)画出△ABC绕点C逆时针旋转90°后得到的△A2B2C,并写出点A2的坐标;
(3)在(2)的条件下,直接写出线段BA在旋转过程中扫过的面积.
20.(8分)如图,已知线段a,b,求作等腰三角形,腰长为b.(a<b,尺规作图,保留作图痕迹)
21.(8分)已知,如图,在▱ABCD中,延长BC到点F,使得AE=CF,分别交AB,CD于点M,N,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
22.(10分)为了加强对校内外的安全监控,创建“平安校园”,某学校计划增加15台监控摄像设备,其中每台价格、有效监控半径如表格所示.经调查,购买1台甲型设备比购买1台乙型设备少150元
甲型
乙型
价格(单位:元/台)
a
b
有效监控半径(单位:米/台)
100
150
(1)求a,b的值;
(2)若购买该批设备的资金不超过7200元,则至少购买甲型设备多少台?
(3)在(2)购买设备资金不超过7200元的条件下,若要求有效监控半径覆盖范围不低于1600米,请你设计一种最省钱的购买方案.
23.(8分)如图,在△ABC中,AB=AC,点E在AC上,且AE=DE
(1)求证:四边形ABFE是平行四边形;
(2)求证:E是AC的中点;
(3)若BD=3,BF=2.5,则四边形ABFE的面积为 .
24.(12分)对于平面直角坐标系xOy中的线段MN及点Q,给出如下定义:
若点Q满足QM=QN,则称点Q为线段MN的“中垂点”;当QM=QN=MN时
(1)如图1,A(4,0),下列各点中,线段OA的中垂点是 .
Q1(0,4),Q2,(2,﹣4),Q3(1,)
(2)如图2,点A为x轴上一点,若Q(2,2),写出线段OQ的两个“完美中垂点”是 和 ,两者的距离是 .
(3)如图3,若点A为x轴正半轴上一点,点Q为线段OA的“完美中垂点”(0,m)在y轴上,在线段PA上方画出线段AP的“完美中垂点”M (用含m的式子表示).并求出∠MQA(写出简单思路即可).
25.(12分)综合与实践:
动手操作:某校八(1)班数学课外兴趣小组在学完第13章的特殊三角形后,利用手头上的一副三角板(DOE=90°,∠E=30°)的直角顶点O放置在另一块直角三角板ABC(∠C=90°,AC=BC)斜边AB的中点处
发现结论:
(1)如图1,三角板DOE的两边DO,EO分别与另一块三角板的边AC,Q(规定:此时点P,Q均在边AC,BC上运动),他们在旋转过程中,发现线段AP与CQ的长总相等及四边形OPCQ的面积不会发生变化.
问题解决:①请你帮他们说明AP=CQ的理由;
②若AB=12cm,请你帮他们求出四边形OPCQ的面积.
拓展延申:
(2)如图2,连接CD,当AB=12cm,那么直角三角板DOE在绕点O旋转一周的过程中,请你直接写出线段CD长的最小值和最大值.
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)历时7年研发建设完成,拥有100%自主知识产权的“云巴”(如图)在重庆璧山正式运行( )
A.对称 B.旋转 C.平移 D.跳跃
【分析】根据平移的定义判断即可.
【解答】解:“云巴”在轨道上的运行可以看作是平移.
故选:C.
【点评】本题考查对平移与旋转的理解及在实际当中的运用.平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的.正确理解平移与旋转的定义是解题的关键.
2.(4分)分式的值为零,则x等于( )
A.1 B.﹣1 C.0 D.0或1
【分析】直接利用分式的值为零,其分子为零分母不为零,进而得出答案.
【解答】解:分式的值为零,
则x6﹣x=0且x﹣1≠2,
解得:x=0.
故选:C.
【点评】此题主要考查了分式的值为零的条件,正确掌握分式的值为零的条件是解题关键.
3.(4分)如图所示,在数轴上表示不等式正确的是( )
A.x<1 B.x≤1 C.x>1 D.x≥1
【分析】根据在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示,可得答案.
【解答】解:由题意,得:x<1,
故选:A.
【点评】本题考查了在数轴上表示不等式的解集,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
4.(4分)下列说法错误的是( )
A.若a>b,则a+3>b+3 B.若a>b,则3﹣2a<3﹣2b
C.若ac2<bc2,则a<b D.若a<b,则
【分析】根据不等式的基本性质,逐项判断即可.
【解答】解:∵a>b,
∴a+3>b+3,
∴选项A不符合题意;
∵a>b,
∴﹣4a<﹣2b,
∴3﹣8a<3﹣2b,
∴选项B不符合题意;
∵若ac8<bc2,则c2>5,
∴<,即a<b,
∴选项C不符合题意;
∵若a<b,则<1(b>3),,
∴选项D符合题意.
故选:D.
【点评】此题主要考查了不等式的基本性质:(1)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;(2)不等式的两边同时乘(或除以)同一个正数,不等号的方向不变;(3)不等式的两边同时乘(或除以)同一个负数,不等号的方向改变.
5.(4分)如图,在同一平面内,将△ABC绕点A逆时针方向旋转30°到△AB′C′,则∠AC′C等于( )
A.60° B.65° C.70° D.75°
【分析】先由旋转得到AC'=AC,∠C'AC=30°,再根据等腰三角形的性质计算即可.
【解答】解:由旋转可知,AC'=AC,
∴∠AC'C=∠ACC'=(180﹣30)°=75°,
故选:D.
【点评】本题考查了旋转的性质,等腰三角形的性质,熟练掌握各知识点是解题的关键.
6.(4分)把多项式m(a﹣2)+(a﹣2)分解因式等于( )
A.m(a﹣2) B.(a﹣2)(m+1) C.m(a+2) D.(m﹣1)(a﹣2)
【分析】首先找出公因式(a﹣2),进而分解因式得出答案.
【解答】解:原式=(a﹣2)(m+1).
故选:B.
【点评】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
7.(4分)下列命题中是真命题的是( )
A.一组边、一组角对应相等的两个直角三角形全等
B.若等腰三角形的两边长分别为5cm,6cm,则该等腰三角形的周长是16cm
C.平行四边形是中心对称图形,两条对角线的交点是它的对称中心
D.三角形中三边的垂直平分线的交点到三边的距离相等
【分析】根据全等三角形的判定定理,等腰三角形的定义,平行四边形的对称性和三角形外心的性质等分别判断即可.
【解答】解:一组边和任一组锐角对应相等的两个直角三角形全等,故A是假命题;
若等腰三角形的两边长分别为5cm,6cm,故B是假命题;
平行四边形是中心对称图形,两条对角线的交点是它的对称中心,符合题意;
三角形中三边的垂直平分线的交点到三个顶点的距离相等,故D是假命题;
故选:C.
【点评】本题考查命题与定理,解题的关键是掌握教材上相关的概念和定理.
8.(4分)如图,在平行四边形ABCD中,对角线AC,E是AD的中点,连接OE.若AC=8,则平行四边形ABCD的周长为( )
A.17 B.20 C.26 D.34
【分析】根据平行四边形的对角线互相平分,得到O是AC的中点,进而得到OE为△ACD的中位线,得到△ACD的周长是△AOE的周长的2倍,用△ACD的周长减去AC的长,得到AD+CD的长,即可得解.
【解答】解:∵平行四边形ABCD的对角线AC,BD相交于点O,
∴OA=OC=AC,
∵点E是AD中点,
∴AE=ED=AD,
∴OE=CD,
∴△ACD的周长=AC+AD+CD=2(AO+OE+AE),
∵△AOE的周长=AO+OE+AE=9,
∴AC+AD+CD=18,
∵AC=5,
∴AD+CD=18﹣8=10,
∴平行四边形ABCD的周长=2(AD+CD)=20,
故选:B.
【点评】本题考查平行四边形的性质,三角形的中位线定理.熟练掌握平行四边形的对角线互相平分,是解题的关键.
9.(4分)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
【分析】由不等式ax+b<0的解是x>﹣2可得直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,进而求解.
【解答】解:∵不等式ax+b<0的解是x>﹣2,
∴直线y=ax+b与x轴交点为(﹣6,0)且y随x增大而减小,
故选:C.
【点评】本题考查一次函数与一元一次不等式的关系.解题关键是将不等式问题转化为图象求解.
10.(4分)如图,四边形ABCD是平行四边形,AE∥BD,连接DE交AB于点F,连接CFEC:②四边形AEBD是平行四边形:③若∠ADF=∠BCF,则∠ABC=90°,则△DCE是直角三角形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据平行四边形的判定与性质、等腰三角形的判定与性质、直角三角形的判定判断求解即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵AE∥BD,
∴四边形AEBD是平行四边形,
故②正确,符合题意;
∴AD=EB,
∴EB=BC,
∵EC=EB+BC,
∴BC=EC,
故①正确,符合题意;
∵AD∥EC,
∴∠ADF=∠FEC,
∵∠ADF=∠BCF,
∴∠FEC=∠BCF,
∴FE=FC,
又∵BC=BE,
∴FB⊥BC,
即∠ABC=90°,
故③正确,符合题意;
∵四边形AEBD是平行四边形,
∴DF=EF,
∵DF=FC,
∴EF=FC,
∴∠ABC=90°,
∵AB∥CD,
∴∠DCE+∠ABC=180°,
∴∠DCE=90°,
∴△DCE是直角三角形,
故④正确,符合题意;
故选:A.
【点评】此题考查了平行四边形的判定与性质,熟记平行四边形的判定定理与性质定理是解题的关键.
二、填空题(本大题共5小题,每小题4分,共20分)
11.(4分)计算:7582﹣2422= 516000 .
【分析】直接利用平方差公式计算,进而得出答案.
【解答】解:7582﹣2422=(758+242)×(758﹣242)
=1000×516
=516000.
故答案为:516000.
【点评】此题主要考查了公式法分解因式,正确运用平方差公式是解题关键.
12.(4分)如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC.若AB=AC=26cm,∠ABC=30°,则AD的长为 13 cm.
【分析】由等腰三角形的性质得AD⊥BC,则∠ADB=90°,再由含30°角的直角三角形的性质即可解答.
【解答】解:∵AB=AC=26cm,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵∠ABC=30°,
∴AD=AB=,
故答案为:13.
【点评】本题考查了解直角三角形的应用,含30°角的直角三角形以及等腰三角形的性质,熟练掌握等腰三角形的性质和含30°角的直角三角形的性质是解题的关键.
13.(4分)如图,∠1,∠2;②∠1+∠3<∠ABC+∠D;③∠1+∠2+∠3=360° ① .(填序号)
【分析】根据多边形的外角和是360°及三角形的外角定理求解判断即可.
【解答】解:如图,连接BD,
∵∠1=∠ABD+∠ADB,∠3=∠DBC+∠BDC,
∴∠7+∠3=∠ABD+∠ADB+∠DBC+∠BDC=∠ABC+∠ADC,
故①正确,②不正确;
∵多边形的外角和是360°,
∴∠1+∠3+∠3<360°,
故③④不正确.
故答案为:①.
【点评】此题考查了多边形的内角与外角,构造三角形的外角是解题的关键.
14.(4分)如图,M,N为4×4方格纸中格点上的两点,若以MN为边(P在格点上),使得△MNP为等腰三角形,则点P的个数为 5 个.
【分析】分三种情况:当MP=MN时,当NP=NM时,当PM=PN时,即可解答.
【解答】解:如图:
分三种情况:
当MP=MN时,以点M为圆心,则点P1,P2即为所求;
当NP=NM时,以点N为圆心,则点P2即为所求;
当PM=PN时,作线段MN的垂直平分线4,P5即为所求;
综上所述:使得△MNP为等腰三角形,则点P的个数为8个,
故答案为:5.
【点评】本题考查了等腰三角形的判定,分三种情况讨论是解题的关键.
15.(4分)如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,其两边分别与OA、OB相交于M、N两点,则以下结论:
①PM=PN恒成立;②△OMN的周长不变;③OM+ON的值不变,其中正确的为 ①③④ (请填写正确结论前面的序号).
【分析】作PE⊥OA于E,PF⊥OB于F.只要证明△POE≌△POF,△PEM≌△PFN,即可一一判断.
【解答】解:如图,作PE⊥OA于E,
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,
∴PE=PF,
在Rt△POE和Rt△POF中,
,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故④正确,
∵OM+ON=OE+ME+OF﹣NF=2OE,
∴OM+ON为定值,故③②正确,
在旋转过程中,△PMN是顶角不变的等腰三角形,
∵PM的长度是变化的,
∴MN的长度是变化的,故错误,
故答案为:①③④.
【点评】本题考查全等三角形的性质、角平分线的性质定理、四边形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
三、解答题(本大题共10小题,共90分)
16.(8分)(1)解分式方程:;
(2)解不等式组,并把解集在数轴上表示出来.
【分析】(1)观察可得最简公分母是(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)先分别求得每个不等式的解集,再找到其公共解集即可.
【解答】解:(1)方程两边都乘以x﹣2得
1﹣x﹣(x﹣2)=﹣3,
解得x=3,
经检验x=6是原方程的根,
∴原方程的根为x=3;
(2),
解不等式①,得x>﹣4,
解不等式②,得x≤2,
∴不等式组的解集为﹣4<x≤6,
把解集在数轴上表示:.
【点评】本题考查解不等式组及解分式方程.用到的知识点为:解不等式组应找到两个不等式的公共解集;分式方程必须验根.
17.(8分)先化简:,再从﹣2.﹣1,0,1中挑一个自己喜欢的整数代入求值.
【分析】先算括号内的式子,再算括号外的除法,然后从﹣2.﹣1,0,1中挑一个使得原分式有意义的值代入化简后的式子计算即可.
【解答】解:
=•
=•
=•
=,
∵当x=1或﹣6时,原分式无意义,
∴x可以取﹣1或0,
当x=8时,原式=.
【点评】本题考查分式的化简求值,熟练掌握运算法则是解答本题的关键.
18.(6分)已知关于x的分式方程=2的解为正数,求m的取值范围.
【分析】表示出分式方程的解,由分式方程的解是正数,求出m的范围即可.
【解答】解:方程两边同乘(x+2)得:
m+x=2x+3,
解得:x=m﹣4,
根据分式方程的解为正数,得到m﹣4>6,
解得:m>4,
∴m的取值范围为m>4.
【点评】此题考查的是分式方程的解,能够正确求得分式方程的解是解决此题关键.
19.(10分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,△ABC的三个顶点A(5,5),B(6,3),C(2,1)均在格点上.
(1)画出将△ABC向下平移4个单位长度得到的△A1B1C1;
(2)画出△ABC绕点C逆时针旋转90°后得到的△A2B2C,并写出点A2的坐标;
(3)在(2)的条件下,直接写出线段BA在旋转过程中扫过的面积.
【分析】(1)根据平移的性质即可画出图形;
(2)根据旋转的性质即可画出图形,从而得出点A2的坐标;
(3)由勾股定理得BA=,再代入扇形面积公式即可.
【解答】解:(1)如图,△A1B1C7即为所求;
(2)如图,△A2B2C即为所求,A8(﹣2,4);
(3)∵A(6,5),3),
∴BA==,
∴线段BA在旋转过程中扫过的面积为=π.
【点评】本题主要考查了作图﹣平移变换,旋转变换,扇形的面积等知识,熟练掌握平移和旋转的性质是解题的关键.
20.(8分)如图,已知线段a,b,求作等腰三角形,腰长为b.(a<b,尺规作图,保留作图痕迹)
【分析】若高为底边上的高:在直线l上取点D,作l′⊥l于D,在l′上截取AD=a,然后以点A为圆心,b为半径画弧交l于B、C两点,则△ABC满足条件.若高为腰上的高:先作AB=b,再作AB的垂中平分线得到AB的中点,接着以AB为直径作圆,再圆上截取BD=a,然后在AD的延长线上(DA的反向延长线上)截取AC=b,则△ABC满足条件.
【解答】解:如图,△ABC为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
21.(8分)已知,如图,在▱ABCD中,延长BC到点F,使得AE=CF,分别交AB,CD于点M,N,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【分析】(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得\;BM4{=}^{∥}\left\{\begin{array}{l}{∠EAM=∠FCN}\\{AE=CF}\\{∠E=∠F}\end{array}\right.{AB}_{=}^{∥}CD{BM}_{=}^{∥}DN$,
∴四边形BMDN是平行四边形.
【点评】本题考查了平行四边形的判定及性质,全等三角形的判定,属于基础题,比较简单.
22.(10分)为了加强对校内外的安全监控,创建“平安校园”,某学校计划增加15台监控摄像设备,其中每台价格、有效监控半径如表格所示.经调查,购买1台甲型设备比购买1台乙型设备少150元
甲型
乙型
价格(单位:元/台)
a
b
有效监控半径(单位:米/台)
100
150
(1)求a,b的值;
(2)若购买该批设备的资金不超过7200元,则至少购买甲型设备多少台?
(3)在(2)购买设备资金不超过7200元的条件下,若要求有效监控半径覆盖范围不低于1600米,请你设计一种最省钱的购买方案.
【分析】(1)根据“购买1台甲型设备比购买1台乙型设备少150元,购买3台甲型设备比购买2台乙型设备多150元”,即可得出关于a,b的二元一次方程组,解之即可得出结论;
(2)设购买甲型设备x台,则购买乙型设备(15﹣x)台,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再结合x为整数即可得出答案;
(3)由(2)的结论结合监控半径覆盖范围不低于1600米,可求出x的值,再利用总价=单价×数量可求出当x=12和x=13时购买费用,比较后即可得出结论.
【解答】解:(1)根据题意,,
解得,
(2)设购买甲型设备x台,则购买乙型设备(15﹣x)台.
根据题意,得450x+600(15﹣x)≤7200,
解得x≥12.
答:至少购买甲型设备12台.
(3)根据题意,得100x+150(15﹣x)≥1600.
解得x≤13,
∴12≤x≤13.
∴x的取值为12或13.
共有两种购买方案:
方案一:购买甲型设备12台,乙型设备5台;
方案二:购买甲型设备13台,乙型设备2台.
∵7200>7050,
∴方案二省钱.
答:最省钱的购买方法为购买甲型设备13台,乙型设备2台.
【点评】本题考查了二元一次方程组的应用、一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)根据各数量之间的关系,正确列出一元一次不等式.
23.(8分)如图,在△ABC中,AB=AC,点E在AC上,且AE=DE
(1)求证:四边形ABFE是平行四边形;
(2)求证:E是AC的中点;
(3)若BD=3,BF=2.5,则四边形ABFE的面积为 12 .
【分析】(1)根据角平分线定义,结合已知条件易得∠BAD=∠ADE,则AB∥EF,然后结合已知条件,利用两组对边分别平行的四边形是平行四边形即可证得结论;
(2)结合已知条件,根据三线合一及平行线分线段成比例即可证得结论;
(3)利用平行四边形性质及线段中点的定义可得AC=5,然后利用三线合一及勾股定理求得AD的长度,再利用平行线性质及全等三角形的判定及性质易证得S△DCE=S△DBF,最后利用面积的和差将平行四边形ABFE的面积转化成△ABC的面积后利用三角形面积公式即可求得答案.
【解答】(1)证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵AE=DE,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥EF,
∵BF∥AC,
∴四边形ABFE是平行四边形;
(2)证明:∵AB=AC,AD是∠BAC的平分线,
∴,
∵DE∥AB,
∴,
∴AE=CE,
∴E是AC的中点;
(3)解:∵四边形ABFE是平行四边形,
∴CE=AE=BF=2.5,
∴AC=6,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,
∵CD=BD=3,
∴,BC=2+3=6,
∵BF∥CE,
∴∠C=∠DBF,∠DEC=∠F,
在△DCE与△DBF中,
,
∴△DCE≌△DBF(AAS),
∴S△DCE=S△DBF,
∴S▱ABFE=S△DBF+S四边形ABDE
=S△DCE+S四边形ABDE
=S△ABC
=BC•AD
=
=12.
【点评】本题主要考查了平行四边形的判定与性质以及等腰三角形的性质、全等三角形的判定与性质,解答本题的关键是利用面积的和差将平行四边形ABFE的面积转化成△ABC的面积.
24.(12分)对于平面直角坐标系xOy中的线段MN及点Q,给出如下定义:
若点Q满足QM=QN,则称点Q为线段MN的“中垂点”;当QM=QN=MN时
(1)如图1,A(4,0),下列各点中,线段OA的中垂点是 Q2 .
Q1(0,4),Q2,(2,﹣4),Q3(1,)
(2)如图2,点A为x轴上一点,若Q(2,2),写出线段OQ的两个“完美中垂点”是 A(4,0) 和 Q′(﹣2,2) ,两者的距离是 4 .
(3)如图3,若点A为x轴正半轴上一点,点Q为线段OA的“完美中垂点”(0,m)在y轴上,在线段PA上方画出线段AP的“完美中垂点”M |m| (用含m的式子表示).并求出∠MQA(写出简单思路即可).
【分析】(1)由“中垂点”定义可求解.
(2)如图,当△AOQ,△OQQ′是等边三角形时,点A和点Q是线段OQ的“完美中垂点”,
(3)如图3中,以PA为边,向上作等边三角形PAM,连接QM.利用全等三角形的性质求解即可.
【解答】解:(1)∵若点Q满足QM=QN,则称点Q为线段MN的“中垂点”;
∴Q在MN的垂直平分线上,
∵线段OA的对称点在OA的垂直平分线上,且A(4,O(0,
∴线段OA的中垂点横坐标为7,
∴Q2(2,﹣4)符合题意,
故答案为Q2.
(2)如图,当△AOQ,点A和点Q是线段OQ的“完美中垂点”,
∴A(4,3),2),
AQ′==4,
故答案为:A(4,0),8),4.
(3)如图3中,以PA为边,连接QM.
∵点Q为线段OA的“完美中垂点”,
∴△AOQ是等边三角形,
∴∠OAQ=∠PAM=60°,
∴∠OAP=∠QAM,
在△OAP和△QAM中,
∴△OAP≌△QAM(SAS),
∴OP=QM=|m|,∠AOP=∠AQM=90°,
故答案为:|m|,90°.
【点评】本题考查等腰三角形的性质,坐标与图形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
25.(12分)综合与实践:
动手操作:某校八(1)班数学课外兴趣小组在学完第13章的特殊三角形后,利用手头上的一副三角板(DOE=90°,∠E=30°)的直角顶点O放置在另一块直角三角板ABC(∠C=90°,AC=BC)斜边AB的中点处
发现结论:
(1)如图1,三角板DOE的两边DO,EO分别与另一块三角板的边AC,Q(规定:此时点P,Q均在边AC,BC上运动),他们在旋转过程中,发现线段AP与CQ的长总相等及四边形OPCQ的面积不会发生变化.
问题解决:①请你帮他们说明AP=CQ的理由;
②若AB=12cm,请你帮他们求出四边形OPCQ的面积.
拓展延申:
(2)如图2,连接CD,当AB=12cm,那么直角三角板DOE在绕点O旋转一周的过程中,请你直接写出线段CD长的最小值和最大值.
【分析】(1)①连接CO,根据等腰直角三角形的性质得到;∠BCO=∠A=45°,CO⊥AB,根据全等三角形的性质得到AP=CQ;
②根据全等三角形的性质和三角形的面积公式即可得到结论;
(2)如图2,当点D,C,O在一条直线上,且点C在点D和点O之间时,线段CD长的最小,如图3,当点D,C,O在一条直线上,且点,O在点D和点C之间时,线段CD长的最大,根据直角三角形的性质即可得到结论.
【解答】解:(1)①理由是:连接CO,
∵△ABC是等腰直角三角形,O是AB的中点,
∴;∠BCO=∠A=45°,
∵∠DOE=90°
∴∠AOP=∠COQ,
在△AOP和△COQ中,
,
∴△AOP≌△COQ(ASA),
∴AP=CQ;
即:AP与CQ的长总相等;
②∵△AOP≌△COQ,
∴S△AOP=S△COQ,
∴S四边形CPOQ=S△COQ+S△COP=S△AOP+S△COP=S△AOC,
∵,
∴S四边形CPOQ=18
即:四边形OPCQ的面积总是一个定值为18;
(2)如图2,当点D,C,且点C在点D和点O之间时,
∵∠DOE=90°,∠E=30°,
∴OD=DE=7cm,
∵AB=12cm,
∴OC=AB=6cm,
∴线段CD长的最小值为OD﹣OC=1;
如图4,当点D,C,且点,线段CD长的最大,
∵∠DOE=90°,∠E=30°,
∴OD=DE=7cm,
∵AB=12cm,
∴OC=AB=3cm,
∴线段CD长的最大值为OD+OC=7+6=13(cm).
【点评】本题是四边形的综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,三角形面积的计算,正确地作出图形是解题的关键.
四川省达州市渠县三江中学2022-2023学年八年级下学期期末数学试卷: 这是一份四川省达州市渠县三江中学2022-2023学年八年级下学期期末数学试卷,共33页。
四川省达州市渠县清溪中学2022-2023学年七年级下学期期末数学试卷: 这是一份四川省达州市渠县清溪中学2022-2023学年七年级下学期期末数学试卷,共28页。试卷主要包含了精心选一选,细心填一填,用心做一做等内容,欢迎下载使用。
四川省达州市渠县琅琊中学2022-2023学年八年级下学期期末数学试卷+: 这是一份四川省达州市渠县琅琊中学2022-2023学年八年级下学期期末数学试卷+,共19页。试卷主要包含了 下列各式中为分式方程的是, 若3-xy=⋅A,则A为等内容,欢迎下载使用。












