




初中数学浙教版八年级上册1.3 证明优秀当堂检测题
展开浙教版数学 八上 第一章 1.3证明测试卷A卷
一. 选择题(共30分)
1.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.45° B.65° C.75° D.85°
【思路点拨】由平角等于180°结合三角板各角的度数,可求出∠2的度数,由直尺的上下两边平行,利用“两直线平行,同位角相等”可得出∠1的度数.
【答案】解:∵∠2+60°+45°=180°,∴∠2=75°.
∵直尺的上下两边平行,∴∠1=∠2=75°.故选:C.
2.小明花整数元网购了一本《趣数学》,让同学们猜书的价格.甲说:“至少15元”,乙说“至多13元”,丙说:“至多10元”.小明说:“你们都猜错了.”则这本书的价格为( )
A.12元 B.13元 C.14元 D.无法确定
解:由题意可得,
甲、乙、丙的说法都是错误的,
甲的说法错误,说明这本书的价格少于15元,
乙、丙的说法错误,说明这本书的价格高于13元,
又因为明花整数元网购了一本《趣数学》,
所以这本书的价格是14元,
故选:C.
3.某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入到最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c且a,b,c均为正整数);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
解:∵甲最后得分为16分,
∴a>4,
接下来以乙为主要研究对象,
①若乙得分名次为:1场第一名,3场第二名,则a+3b=8,
则3b=8﹣a<4,而bb为正整数,
则b=1,又cc为正整数,a>b>c,
此时不合题意;
②若乙得分名次为:1场第一名,2场第二名,1场第三名,
则a+2b+c=8,
则2b+c=8﹣a<4,
由a>b>c,且a,b,c为正整数可知,
此时没有符合该不等式的解,
不符合题意;
③若乙得分名次为:1场第一名,1场第二名,2场第三名,
则a+b+2c=8,则b+2c=8﹣a<4,
由a>b>c,且a,b,cc为正整数可知,
此时没有符合该不等式的解,不符合题意;
④若乙得分名次为:1场第一名,3场第三名,
则a+3c=8,此时显然a=5,c=1,
则甲的得分情况为3场第一名,1场第三名,共3×5+1=16分,
乙的得分情况为1场第一名,3场第三名,共5+3×1=8分,
丙的得分情况为4场第二名,则4b=8,即b=2,
此时符合题意.
综上分析可知,乙在四场比赛中没有获得过第二名.
故选:C.
4.老师让4个学生猜一猜这次考试中4个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗?( )
A.甲 B.乙 C.丙 D.丁
解:假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好,
故选:C.
5.有甲、乙、丙三人,甲说乙在说谎,乙说丙在说谎,丙说甲和乙都在说谎,则( )
A.甲说实话,乙和丙说谎 B.乙说实话,甲和丙说谎
C.丙说实话,甲和乙说谎 D.甲、乙、丙都说谎
解:A、若甲说的是实话,即乙说的是谎话,则丙没有说谎,即甲、乙都说谎是对的,与甲说的是实话相矛盾,故A不合题意;
B、若乙说的是实话,即丙说的谎话,即甲、乙都说谎是错了,即甲,乙至少有一个说了实话,与乙说的是实话不矛盾,故B符合题意;
C、若丙说的是实话,甲、乙都说谎是对的,那甲说的乙在说谎是对的,与丙说的是实话相矛盾,故C不合题意;
D、若甲、乙、丙都说谎,与丙说的甲和乙都在说谎,相矛盾,故D不合题意;
故选:B.
6.已知,,是不完全相等的任意实数,,,,则关于,,的值,下列说法正确的是
A.都大于0 B.都小于0
C.至少有一个大于0 D.至多有一个大于0
解:因为,
所以,,.不能都大于0,也不能都小于0,
所以排除和;
又因为,,是不完全相等的任意实数,
所以,,不能同时为0,
所以至少有一个是正数,也可以有两个是正数,
所以排除,
所以选.
故选:.
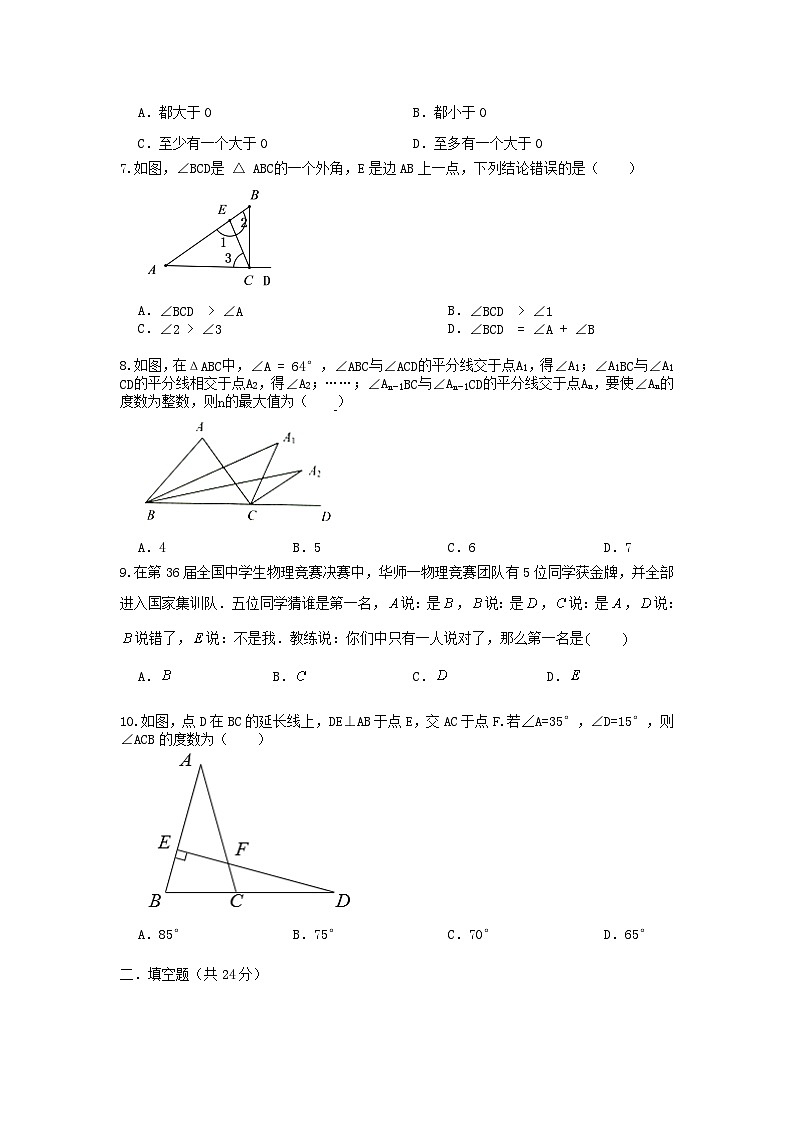
7.如图,∠BCD是△ABC的一个外角,E是边AB上一点,下列结论错误的是( )
A.∠BCD>∠A B.∠BCD>∠1
C.∠2>∠3 D.∠BCD=∠A+∠B
【答案】B
【解析】A、∠BCD是△ABC的一个外角,则∠BCD>∠A,不符合题意.
B、∠BCD是△ABC的一个外角,则∠1是△BEC的一个外角,∠BCD与∠1无法比较大小,符合题意.
C、∠2是△AEC的一个外角,则∠2>∠3,不符合题意.
D、∠BCD是△ABC的一个外角,则∠BCD=∠A+∠B,不符合题意.
故答案为:B.
8.如图,在ΔABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An−1BC与∠An−1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
A.4 B.5 C.6 D.7
【答案】C
【解析】由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=12∠ABC,∠A1CD=12∠ACD,
∴∠A1+∠A1BC=12(∠A+∠ABC)=12∠A+∠A1BC,
∴∠A1=12∠A=12×64°=32°;
∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1,
∴∠A1=12∠A,
同理可得∠A1=2∠A2,
∴∠A2=14∠A,
∴∠A=2n∠An,
∴∠An=(12)n∠A=64°2n,
∵∠An的度数为整数,
∵n=6.
故答案为:C.
9.在第36届全国中学生物理竞赛决赛中,华师一物理竞赛团队有5位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,说:是,说:是,说:是,说:说错了,说:不是我.教练说:你们中只有一人说对了,那么第一名是
A. B. C. D.
解:说:是,说:说错了,教练说:你们中只有一人说对了,所以和的说法只能一真一假,不能同真,也不能同假;
所以和,说得都是假话,
所以只有说对了,
答:第一名是.
故选:.
10.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.85° B.75° C.70° D.65°
【答案】C
【解析】∵DE⊥AB,∠A=35°,
∴∠CFD=∠AFE=90°-∠A=90°-35°=55°,
又∵∠D=15°,
∴∠ACB=∠D+∠CFD=15°+55°=70°.
故答案为:C.
二. 填空题(共24分)
11.今年长沙马拉松中三名参赛者甲、乙、丙.他们来自不同职业:医生,教师,会计.已知甲和医生不同年龄,丙比会计年轻,医生比乙年长.则甲的职业是 .
解:记已知条件为①,②,③,
由①知甲不是医生,由③知乙也不是医生,故知丙是医生,
假定甲是教师,则乙应是会计,
但由②知丙比乙年轻,由③又得丙比乙年长,两者矛盾,故甲不是教师,
∴甲是会计.
故答案为:会计.
12.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是 .
①
6
9
0
只有一个号码正确且位置正确
②
2
5
6
只有两个号码正确且位置不正确
③
8
6
9
三个号码都不正确
解:根据③知密码里不含有8,6,9,
∴①中只有0正确,且位置正确,
∵②中有两个号码正确且位置不正确,
∴2和5数字正确,且位置不正确,
所以该密码里含有2,5,0三个数字,位置确定为520,
故答案为:520.
13.如图,在△ABC中,∠ACB=68°,∠1=∠2.若P为△ABC的角平分线BP、CP的交点,则∠BPC= °.
【思路点拨】首先根据∠ACB=68°可得∠1+∠PCB=68°,再根据等量代换和三角形的内角和可得答案.
【答案】解:∵∠ACB=68°,∴∠1+∠PCB=68°,∵∠1=∠2,∴∠2+∠PCB=68°,
∴∠BPC=180°﹣(∠2+∠PCB)=112°.故答案为:112
14.如图,把△ABC沿线段DE折叠,使点A落在线段BC上的点F处,BC∥DE,若∠A+∠B=106°,则∠FEC= 度.
【分析】根据三角形内角和定理和平行线的性质即可求出结果.
【解析】由折叠可知:∠AEF=2∠AED=2∠FED,
∵∠A+∠B=106°,∴∠C=180°﹣106°=74°,
∵BC∥DE,∴∠AED=∠C=74°,
∴∠AEF=2∠AED=148°,∴∠FEC=180°﹣∠AEF=32°.故答案为:32.
15.如图,∠BDC,∠BEC的大小关系是∠BDC ∠BEC(填>,=或<).
【答案】<
【解析】∵∠BDC是△BDE的内角,∠BEC是△BDE的外角,
∴∠BDC<∠BEC,
故答案为:<.
16.一副直角三角板,按如图所示的方式摆放,D,F在边AB上,点C在边DE上,EF,AC相交于点G,∠A=30°,∠E=45°,则∠FGA的度数为 .
【答案】15°
【解析】∵△DEF是直角三角形,∠E=45°,∠A=30°,
∴∠DFE=45°,
∵∠DFE=∠A+∠FGA,
∴∠FGA=∠DFE−∠A=45°−30°=15°,
故答案为:15°.
三, 解答题(共66分)
17.(8分)某次数学竞赛中有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个是正确的.如表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题
第二题
第三题
第四题
第五题
得分
甲
C
C
A
B
B
4
乙
C
C
B
B
C
3
丙
B
C
C
B
B
2
丁
B
C
C
B
A
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 CACCC (写出一种即可)
解:(1)∵有5道选择题,每题1分,
甲、乙、丙各得4,3,2分,
观察表格可知:第二题选C和第四题选B,甲、乙、丙、丁四位同学都正确,
所以丙同学答对第二题和第四题,得2分;
第一题选C,甲和乙同学都正确,
所以乙同学答对了第一、第二、第四题,得3分;
通过第三题可知:
乙,丙同学选B,C都答错了,
所以选项A正确,
所以第三题选A;
通过第五题,乙、丙两位同学选C和B都错误,
所以选A正确,
所以甲同学错的是第五题;
故答案为:五;
(2)因为五个题的正确答案是:C、C、A、B、A,
所以丁同学答对了第二、四、五题,
所以丁同学得分是3分.
故答案为:3;
(3)如果有一个同学得了1分,他的答案可能是:C、A、C、C、C(答案不唯一).
故答案为:C、A、C、C、C.
18.(8分)已知△ABC中,AD⊥BC于点D,AE平分∠BAC,过点A作直线GH∥BC,且∠GAB=64°,∠C=42°.
(1)求△ABC的外角∠CAF的度数;
(2)求∠DAE的度数.
【答案】(1)解:∵GH∥BC,∠C=42°,
∴∠HAC=∠C=42°,
∵∠FAH=∠GAB=64°,
∴∠CAF=∠HAC+∠FAH=106°;
(2)解:∵∠HAC=42°,∠GAB=64°,
∴∠BAC=74°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=37°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=42°,
∴∠DAC=90°−42°=48°,
∴∠DAE=∠DAC−∠CAE=48°−37°=11°.
19.(10分)如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为 (只填序号),并说明理由;
①∠DAE=∠1 ②∠DAE=2∠1 ③∠1=2∠DAE
(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.
【思路点拨】(1)根据三角形外角的性质,得∠1=∠EAD+∠EA′D.由题意得:∠DAE=∠DA′E,可推断出∠1=2∠DAE.
(2)如图2,连接AA′.由三角形外角的性质,得∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D.由题意知:∠EAD=∠EA′D,进而推断出∠1+∠2=2∠EAD.
【答案】解:(1)由题意得:∠DAE=∠DA′E.
∵∠1=∠EAD+∠EA′D=2∠DAE.故答案为:③.
(2)∠1+∠2=2∠DAE,理由如下:如图2,连接AA′.
由题意知:∠EAD=∠EA′D.∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,
∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.
20.(10分)小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
【分析】【习题回顾】根据三角形的外角的性质证明;
【变式思考】根据角平分线的定义、直角三角形的性质解答;
【探究延伸】同(1)、(2)的方法相同.
【解答】【习题回顾】证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD,
∵AE是角平分线,∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,∴∠CEF=∠CFE;
【变式思考】∠CEF=∠CFE
证明:∵AF为∠BAG的角平分线,∴∠GAF=∠DAF,
∵CD为AB边上的高,∴∠ACB=90°,
∴∠ADF=∠ACE=90°,又∵∠CAE=∠GAF,∴∠CEF=∠CFE;
【探究延伸】∠M+∠CFE=90°,
证明:∵C、A、G三点共线 AE、AN为角平分线,
∴∠EAN=90°,又∵∠GAN=∠CAM,∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,∴∠M+∠CFE=90°
21.(10分)如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为 (只填序号),并说明理由;
①∠DAE=∠1 ②∠DAE=2∠1 ③∠1=2∠DAE
(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.
【思路点拨】(1)根据三角形外角的性质,得∠1=∠EAD+∠EA′D.由题意得:∠DAE=∠DA′E,可推断出∠1=2∠DAE.
(2)如图2,连接AA′.由三角形外角的性质,得∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D.由题意知:∠EAD=∠EA′D,进而推断出∠1+∠2=2∠EAD.
【答案】解:(1)由题意得:∠DAE=∠DA′E.
∵∠1=∠EAD+∠EA′D=2∠DAE.故答案为:③.
(2)∠1+∠2=2∠DAE,理由如下:如图2,连接AA′.
由题意知:∠EAD=∠EA′D.∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,
∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.
初中数学1.3 证明优秀同步训练题: 这是一份初中数学1.3 证明优秀同步训练题,文件包含答案2docx、原卷2docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
数学1.2 定义与命题精品课后复习题: 这是一份数学1.2 定义与命题精品课后复习题,文件包含答案docx、原卷docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
初中数学浙教版八年级上册1.1 认识三角形精品课后作业题: 这是一份初中数学浙教版八年级上册1.1 认识三角形精品课后作业题,文件包含答案2docx、原卷2docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。













