2023九年级数学上册第28章圆28.3圆心角和圆周角课时3圆内接四边形上课课件新版冀教版

这是一份2023九年级数学上册第28章圆28.3圆心角和圆周角课时3圆内接四边形上课课件新版冀教版，共21页。

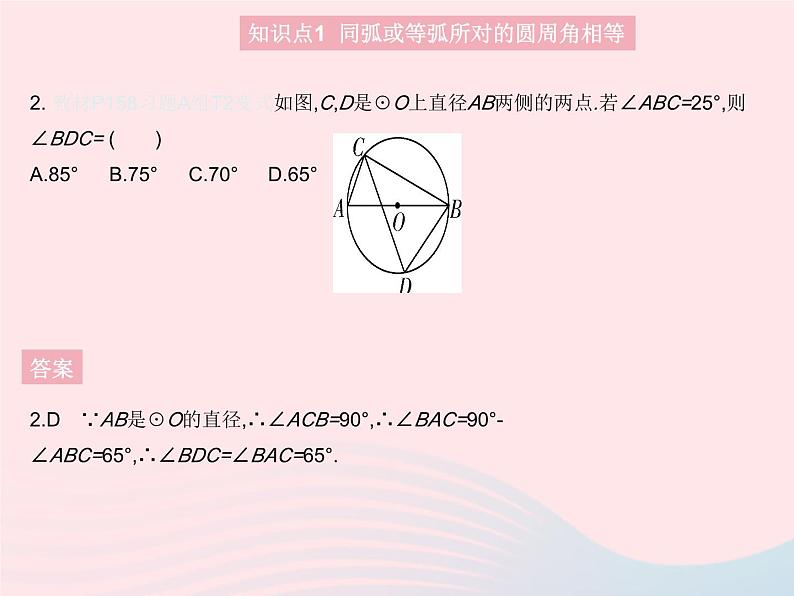
课时3 圆内接四边形1. 一题多解[2022信阳期中]如图,在☉O中,弦AB与CD交于点M,∠C=45°,∠AMD=75°,则∠D的度数是 (　　)A.15° B.25° C.30° D.75°答案1.C　解法一　∵∠C=45°,∴∠B=45°.∵∠AMD=75°,∠B+∠D=∠AMD,∴∠D=75°-45°=30°.解法二　∵∠C=45°,∠AMD=75°,∴∠A=30°,∴∠D=∠A=30°.知识点1 同弧或等弧所对的圆周角相等2. 教材P158习题A组T2变式如图,C,D是☉O上直径AB两侧的两点.若∠ABC=25°,则∠BDC= (　　)A.85° B.75° C.70° D.65°答案2.D　∵AB是☉O的直径,∴∠ACB=90°,∴∠BAC=90°-∠ABC=65°,∴∠BDC=∠BAC=65°.知识点1 同弧或等弧所对的圆周角相等 答案 知识点1 同弧或等弧所对的圆周角相等 答案 知识点1 同弧或等弧所对的圆周角相等5. 如图,在☉O中,直径AB=10,∠ACB的平分线与☉O交于点D,则弦AD的长为　　　　. 答案 知识点1 同弧或等弧所对的圆周角相等6. [2021重庆中考A卷]如图,四边形ABCD内接于☉O,若∠A=80°,则∠C的度数是 (　　)A.80° B.100° C.110° D.120°答案6.B　根据圆内接四边形的对角互补可知,∠C=180°-∠A=180°-80°=100°.知识点2 圆内接四边形的对角互补7. 如图,已知四边形ABDC是☉O的内接四边形,∠1=112°,则∠CDE= (　　)A.56° B.68° C.66° D.58°答案 知识点2 圆内接四边形的对角互补8. [2021海南中考]如图,四边形ABCD是☉O的内接四边形,BE是☉O的直径,连接AE.若∠BCD=2∠BAD,则∠DAE的度数是 (　　)A.30° B.35° C.45° D.60°答案8.A　∵四边形ABCD是☉O的内接四边形,∴∠BAD+∠C=180°,又∵∠C=2∠BAD,∴∠BAD=60°.∵BE是☉O的直径,∴∠BAE=90°,∴∠DAE=∠BAE-∠BAD=90°-60°=30°.知识点2 圆内接四边形的对角互补9. 如图,☉O的内接四边形ABCD的两组对边的延长线分别交于点E,F.(1)若∠E=∠F,则∠ADC=　　　°; (2)当∠A=55°,∠E=30°时,求∠F的度数.答案9.解:(1)90∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,∠ABC=∠BCF+∠F,∴∠ADC=∠ABC.∵四边形ABCD是☉O的内接四边形,∴∠ADC+∠ABC=180°,∴∠ADC=90°.(2)在△ABE中,∠A=55°,∠E=30°,∴∠ABE=180°-∠A-∠E=95°,∴∠ADF=180°-∠ABE=85°,∴∠F=180°-∠ADF-∠A=40°.知识点2 圆内接四边形的对角互补 答案1.D　如图,连接OC,AB.∵A(0,4),∴OA=4.∵∠AOB=90°,∴AB为☉C的直径.∵∠BMO=120°,∴∠BAO=60°.∵AC=OC,∴△AOC是等边三角形,∴OC=OA=4. 答案 3. [2021唐山路北区一模]如图,已知点A,B,C,D在☉O上,圆心O在∠D内部,四边形ABCO为平行四边形,则∠DAO与∠DCO的度数和是 (　　)A.60° B.45° C.35° D.30°答案 4. 原创题如图,将三角尺放在☉O上,且含30°角的两边过圆上的两定点A,B,这两边与圆的另两个交点分别为C,D,移动三角尺保持30°角(∠P)的两边始终过A,B两点,则弦CD的长 (　　)A.随OP的增大而增大B.随OP的增大而减小C.保持不变D.有时增大有时减小答案  答案 6. [2022杭州启航中学期中]如图,△ABC内接于☉O,AF是☉O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF.(1)求证:AE是☉O的直径.(2)若∠ABC=∠EAC,AE=8,求AC的长.答案   答案7.(1)解:∵AB=AC,∴∠ABC=∠ACB=70°,∴∠BAC=180°-2×70°=40°,∴∠BEC=∠BAC=40°.