






初中华师大版22.1 一元二次方程作业课件ppt
展开分层练透教材 多重拓展培优
数学·华师版·九年级上册
第22章 一元二次方程
22.1 一元二次方程
知识点1 一元二次方程的定义
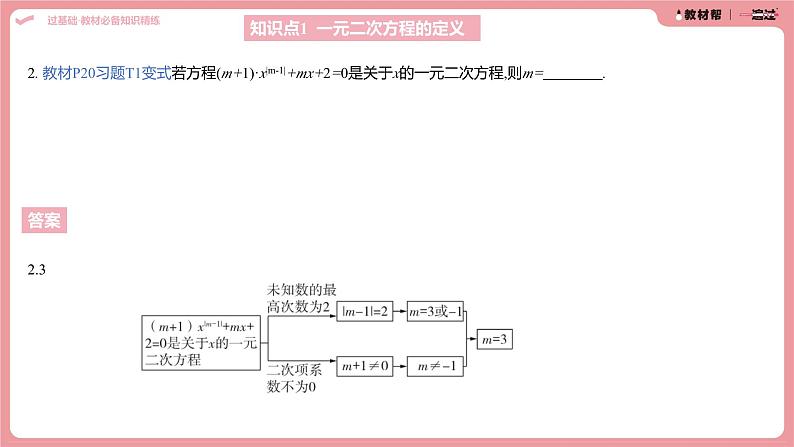
2. 教材P20习题T1变式若方程(m+1)·x|m-1|+mx+2=0是关于x的一元二次方程,则m= .
3. [2021北京海淀区期中]一元二次方程2x2+3x-4=0的一次项系数是 ( )A.-4B.-3C.2D.3
知识点2 一元二次方程的一般形式
4. 方程9x2=8x+2化为一般形式后的二次项、一次项、常数项分别是 ( )A.9x2,8x,2B.-9x2,-8x,-2C.9x2,-8x,-2D.9x2,-8x,2
5. 将下列一元二次方程化为一般形式,并指出方程的二次项系数、一次项系数和常数项.(1)3x=1-2x2; (2)5x(x-2)=4x2-3x.
5.解:(1)3x=1-2x2化为一般形式为2x2+3x-1=0,二次项系数为2,一次项系数为3,常数项为-1.(2)5x(x-2)=4x2-3x化为一般形式为x2-7x=0,二次项系数为1,一次项系数为-7,常数项为0.
6. [2022济宁期末]若关于x的方程x2+ax+a=0有一个根为-2,则a的值是 ( )A.4B.-2C.-3D.-4
知识点2 一元二次方程的根
6.A 把x=-2代入x2+ax+a=0,得(-2)2+(-2)a+a=0,解得a=4.
7. [2022泰州期中]若m是方程x2-x-1=0的一个根,则m2-m+2 022的值为( )A.2 021 B.2 022C.2 023 D.2 024
7.C 把x=m代入x2-x-1=0,得m2-m-1=0,∴m2-m=1,∴m2-m+2 022=1+2 022=2 023.
8. 已知x=1是一元二次方程x2+ax+b=0的一个根,则a2+2ab+b2的值为 .
8.1 ∵x=1是一元二次方程x2+ax+b=0的一个根,∴1+a+b=0,∴a+b=-1,∴a2+2ab+b2=(a+b)2=(-1)2=1.
9. 原创题国家统计局统计数据显示:2021年8月份,社会消费品零售总额为34 395亿元;9月份,社会消费品零售总额为36 833亿元;10月份,社会消费品零售总额为40 454亿元.设2021年8月份到10月份社会消费品零售总额的月平均增长率为x,则可列方程为( )A.36 833(1+x) =40 454B.34 395(1+x)2 =40 454C.34 395(1+2x)=40 454D.34 395+36 833+36 833(1+x)=40 454
知识点3 列一元二次方程
10. [2022武汉期中]如图是一幅黄山迎客松风景图画,该图画长80 cm,宽50 cm,要在它的四周镶一条同样宽的金色纸边,制成一幅长方形挂图.若整个挂图的面积是5 400 cm2,设金色纸边的宽为x cm,则可列方程为 .(写成一般形式)
10.x2+65x-350=0 依题意,得(80+2x)·(50+2x)=5 400,整理,得x2+65x-350=0.
1. [2021牡丹江中考]关于x的一元二次方程(m-3)x2+m2x=9x+5化为一般形式后不含一次项,则m的值为 ( ) A.0B.±3C.3D.-3
1.D 整理(m-3)x2+m2x=9x+5,得(m-3)x2+(m2-9)x-5=0.由题意,得m-3≠0,m2-9=0,所以m=-3.
2. [2022驻马店期中]某厂家2021年8~12月份的口罩产量统计如图所示.设从9月份到11月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程 ( )A.180(1-x)2=461B.180(1+x)2=461 C.368(1-x)2=442D.368(1+x)2=442
3. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为 ( )A.1B.-1C.0D.-2
3.A 因为关于x的一元二次方程x2+ax+b=0有一个非零根-b,所以b2-ab+b=0,所以b(b-a+1)=0,又由题意知b≠0,所以b-a+1=0,所以a-b=1.
4. [2022成都期中]若a是方程3x2-5x+2=0的一个根,则-6a2+10a-5= .
4.-1 根据题意得,3a2-5a+2=0,∴3a2-5a=-2,∴-6a2+10a-5=-2(3a2-5a)-5=-2×(-2)-5=-1.
5. 数学文化 教材P20习题T3变式我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如图,若设正方形的边长是x步,则列出的方程是 .
6. [2022江门期中]在解关于x的一元二次方程x2+bx+c=0时,小明看错了一次项系数b,得到的解为x1=2,x2=3;小刚看错了常数项c,得到的解为x1=1,x2=4.请你写出正确的一元二次方程: .
7. 若正数a是关于x的一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,求a的值.
7.解:因为正数a是关于x的一元二次方程x2-5x+m=0的一个根,所以a2-5a+m=0 ①;因为-a是关于x的一元二次方程x2+5x-m=0的一个根,所以a2-5a-m=0 ②.由①+②得,2a2-10a=0,所以a2=5a.又因为a是正数,所以a=5.
8. [2021上海徐汇区期中]根据题意,列出方程:(不必求解)如图,用木板靠墙(墙足够长)建一个面积为100 m2的长方形仓库,并在与墙平行的一边开一道宽1 m的门.现有长28 m的木板,求仓库中与墙垂直的一面的长.
8.解:设仓库中与墙垂直的一面的长为x m,则与墙平行的一面的长为(28-2x+1)m,依题意,得x(28-2x+1)=100,整理得2x2-29x+100=0.
9. 已知关于x的方程ax2+bx+c=0(a≠0),请直接写出方程在下列条件下的一个根:(1)a+b+c=0; (2)a-b+c=0; (3)c=0;(4)4a-2b+c=0; (5)9a+3b+c=0.
9.解:(1)x=1.(2)x=-1.(3)x=0.(4)x=-2.(5)x=3.
课时1 直接开平方法
22.2 一元二次方程的解法
1. [2022唐山期中]张老师给出方程x2-4=0,四位同学给出了以下答案.小丽:x=2.子航:x=-2.一帆:x1=2,x2=-2.萱萱:x=±4.那么答案正确的是 ( ) A.小丽B.子航C.一帆D.萱萱
知识点1 用直接开平方法解形如x2=p(p≥0)的一元二次方程
1.C 将方程x2-4=0移项,得x2=4,两边直接开平方,得x1=2,x2=-2,所以一帆的答案正确.
3. [2021枣庄山亭区期中]下列方程没有实数根的是 ( )A.x2-1=0 B.x2=0C.x2+4=0D.-x2+3=0
3.C 选项A中,x2-1=0,即x2=1,解得x=±1.选项B中,x2=0,解得x=0.选项C中,x2+4=0,即x2=-4<0,所以x2+4=0没有实数根.选项D中,-x2+3=0,即x2=3,解得x=±3.
4. 一题多解若关于x的一元二次方程x2+a=0的一个根是x=-1,则另一个根是 .
5. 易错题如果(a2+b2+1)(a2+b2-1)=63,那么a2+b2的值为 .
5.8 设a2+b2=x,则(x+1)(x-1)=63,整理得x2=64,解得x=±8,即a2+b2=8或a2+b2=-8(不合题意,舍去),所以a2+b2的值为8.
7. 用直接开平方法解下列方程:(1)4x2-9=0; (2)2x2+3=-2x2+2.
知识点2 用直接开平方法解形如(mx+n)2=p(p≥0)的一元二次方程
9. 若关于x的一元二次方程(x+3)2=c有实数根,则c的值可以为 .(写出一个即可)
9.5(答案不唯一,提示:c≥0即可)
10. [2022盐城景山中学期中]如图是一个计算程序,当输出值y=25时,输入值x为 .
10.-4或6 由题意,得(x-1)2=25,所以x-1=±5.当x-1=5时,解得x=6;当x-1=-5时,解得x=-4.
11. 原创题若关于x的方程(mx+1)2-9=0的一个根为1,则m的值为 .
11.2或-4 将x=1代入(mx+1)2-9=0,得(m+1)2-9=0,所以m+1=±3,所以m1=2或m2=-4.
12. 一题多解已知关于x的方程a(x+c)2+b=0(a,b,c为常数,a≠0)的两根分别为x1=-2,x2=1,那么关于x的方程a(x+c-2)2+b=0的两根分别为 .
课时2 因式分解法
知识点1 ab= 0型直接求解
2. 若关于x的一元二次方程的两个根分别为-5,7,则该方程可以是 ( )A.(x+5)(x-7)=0B.(x-5)(x+7)=0C.(x+5)(x+7)=0D.(x-5)(x-7)=0
3. [2022遂宁期中]一元二次方程x2=2x的根为 ( )A.x=0 B.x=2C.x=0或x=2D.x=0或x=-2
知识点2 用提公因式法解一元二次方程
3.C ∵x2=2x,∴x2-2x=0,则x(x-2)=0,∴x=0或x-2=0,解得x1=0,x2=2.
4. [2022扬州江都区期中]一元二次方程x(x+4)=3x+12的根是 .
4.x1=3,x2=-4 由x(x+4)=3x+12,得x(x+4)-3(x+4)=0,所以(x-3)(x+4)=0,所以x-3=0或x+4=0,解得x1=3,x2=-4.
5. 用提公因式法解下列方程:(1)2x2+3x=0; (2)x(x+2)-3x=0.
6. [2021嘉兴中考]小敏与小霞两位同学解方程3(x-3)=(x-3)2的过程如下框: 你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.
6.解:小敏:×.小霞:×.正确的解答过程如下:3(x-3)=(x-3)2,移项,得3(x-3)-(x-3)2=0,提取公因式,得(x-3)(3-x+3)=0,则x-3=0或3-x+3=0,解得x1=3,x2=6.
7. 一元二次方程x2+2x+1=0的根是 ( )A.x1=1,x2=-1B.x1=x2=1C.x1=x2=-1D.x1=-1,x2=2
知识点3 用乘法公式分解因式解一元二次方程
7.C 因为x2+2x+1=0,所以(x+1)2=0,解得x1=x2=-1.
8. [2022河源期中]当x= 时,代数式(x-2)2与(2x+5)2的值相等.
8.-1或-7 根据题意得,(x-2)2=(2x+5)2,整理得,(x-2)2-(2x+5)2=0,所以(x-2+2x+5)[(x-2)-(2x+5)]=0,所以(3x+3)(-x-7)=0,所以x1=-1,x2=-7.
9. 用因式分解法解下列方程:(1)4(x+3)2-(x-2)2=0;(2)(2x+1)2+4(2x+1)+4=0.
1. [2021丹东中考]若实数k,b是一元二次方程(x+3)(x-1)=0的两个根,且k
2. 若方程x2-2px+3q=0的两根分别是-3和5,则多项式2x2-4px+6q可以分解为 .
2.2(x+3)(x-5) 由题意,得2x2-4px+6q=2(x2-2px+3q)=2(x+3)(x-5).
3. [2022宿迁期中]对于实数a,b,定义运算“◎”如下:a◎b=(a+b)2-(a-b)2.若(m+2)◎(m-3)=24,则m= .
3.-3或4 根据题意,得[(m+2)+(m-3)]2-[(m+2)-(m-3)]2=24,整理,得(2m-1)2-49=0.把方程左边分解因式,得(2m-1-7)(2m-1+7)=0,即(2m-8)(2m+6)=0,所以 2m-8=0或2m+6=0,解得m1=4,m2=-3.
(2)3x3-12x2+12x=0可化为3x(x2-4x+4)=0,方程左边分解因式,得3x(x-2)2=0,所以3x=0或(x-2)2=0,得x1=0,x2=x3=2.
5. 一个直角三角形的三条边的长为连续正整数,求此直角三角形的周长.
5.解:设该直角三角形三条边的长分别为x-1,x,x+1(x>1).根据题意,得x2+(x-1)2=(x+1)2,整理,得x2-4x=0,∴x(x-4)=0,∴x1=4,x2=0(舍去),∴x-1=3,x+1=5.3+4+5=12.故此直角三角形的周长为12.
素养提升6. [2022荆州期末]我们知道可以用公式x2+(p+q)x+pq=(x+p)(x+q)来分解因式.例如:(1)x2+6x+8=0,方程左边分解因式得 =0, (2)x2-7x-30=0,方程左边分解因式得 =0. 爱钻研的小明同学发现二次项系数不是1的方程也可以借助此方法求解.如:3x2-7x+2=0.解:方程左边分解因式得(x-2)(3x-1)=0,从而可以快速求出方程的解.请你利用此方法尝试解方程4x2-8x-5=0.
1. 将代数式x2+6x+2化成(x+p)2+q的形式为 ( ) A.(x-3)2+11B.(x+3)2-7C.(x+3)2-11D.(x+2)2+4
1.B x2+6x+2=x2+6x+9-9+2=(x+3)2-7.
2. 请在下面的横线上填上一个合适的数,使式子为完全平方式.(1)x2-4x+ =(x- )2; (2)x2+x+ =(x+ )2; (3)x2-5x+ =(x- )2.
3. [2022武汉硚口区期中]将一元二次方程x2-8x-5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是 ( )A.-4,21B.-4,11C.4,21D.-8,69
知识点2 用配方法解二次项系数为1的一元二次方程
3.A x2-8x-5=0,移项,得x2-8x=5,配方,得x2-8x+16=5+16,即(x-4)2=21,所以a=-4,b=21.
5. 已知方程x2-6x+q=0可以配方成(x-p)2=7的形式,则p+q的值为 .
5.5 ∵x2-6x+q=0,∴x2-6x=-q,∴x2-6x+9=9-q,即(x-3)2=9-q.根据题意知p=3,9-q=7,∴p=3,q=2,∴p+q=3+2=5.
知识点3 用配方法解二次项系数不为1的一元二次方程
9. [2022南昌期中]在解方程2x2+4x+1=0时,对方程进行配方,文本框①中是甲做的,文本框②中是乙做的,则正确的是 .(填序号)
11. 若代数式M=3x2+8,N=2x2+4x,则M与N的大小关系是 ( )A.M≥NB.M≤NC.M>ND.M
11.C ∵M=3x2+8,N=2x2+4x,∴M-N=3x2+8-(2x2+4x)=x2-4x+8=(x-2)2+4.∵(x-2)2≥0,∴(x-2)2+4>0,∴M-N>0,∴M>N.
12. [2022洛阳期中]已知代数式-2x2+4x-18.用配方法说明无论x取何值,此代数式的值总是负数.
12.解:因为-2x2+4x-18=-2(x2-2x+9)=-2(x2-2x+1-1+9)=-2(x-1)2-16,-2(x-1)2≤0,所以-2(x-1)2-16<0,所以无论x取何值,代数式-2x2+4x-18的值总是负数.
1. [2020张家界中考]已知等腰三角形的两边长分别是一元二次方程x2-6x+8=0的两根,则该等腰三角形的底边长为 ( )A. 2B. 4C. 8D. 2或4
1.A 配方,得x2-6x+9=1,即(x-3)2=1,直接开平方,得x-3=±1,所以x1=4,x2=2.当等腰三角形的三边长分别为2,2,4时,不符合三角形三边关系定理,此时不能组成三角形;当等腰三角形的三边长分别为2,4,4时,符合三角形三边关系定理,此时能组成三角形,所以三角形的底边长为2.
2. [2022惠州期中]不论x,y为任何实数,代数式x2+y2+2x-4y+7的值 ( )A.总不小于2B.总不小于7C.可为任何实数D.总为负数
2.A 因为x2+y2+2x-4y+7=(x2+2x+1)+(y2-4y+4)+2=(x+1)2+(y-2)2+2≥2,所以不论x,y为任何实数,代数式x2+y2+2x-4y+7的值总不小于2.
4. 小华设计了一个魔术盒,将任意实数对(a,b)放入其中,会得到一个新的实数a2-2b-3.若将实数对(2x,-x)放入其中得到实数-1,则x的值为 .
5. [2022济宁月考]已知△ABC的三边长a,b,c都是正整数,且满足2a2+b2-4a-6b+11=0,则△ABC的周长是 .
5.7 ∵2a2+b2-4a-6b+11=0,∴2a2-4a+2+b2-6b+9=0,∴2(a-1)2+(b-3)2=0,∴a-1=0,b-3=0,∴a=1,b=3,则3-1
一题练透 利用配方法求解最值问题
问题4:解:由x2+3x+y-3=0,得y=-x2-3x+3,所以y-x=-x2-3x+3-x=-x2-4x+3=-(x2+4x+4-4)+3=-(x+2)2+7,因为-(x+2)2≤0,所以-(x+2)2+7≤7,所以y-x的最大值为7.问题5:解:由题意,得花园的面积是y(20-2y)=-2y2+20y.-2y2+20y=-2(y2-10y+25-25)=-2(y-5)2+50,因为-2(y-5)2≤0,所以-2(y-5)2+50≤50,所以当y=5时,-2y2+20y有最大值,最大值为50,此时20-2y=10<15,符合题意,所以当y=5时,花园的面积最大,最大面积是50 m2.
1. 易错题 用公式法解一元二次方程3x2+3=-2x时,首先要确定a,b,c的值,下列叙述正确的是 ( ) A.a=3,b=2,c=3B.a=-3,b=2,c=3C.a=3,b=2,c=-3D.a=3,b=-2,c=3
1.A 将方程3x2+3=-2x化为一般形式,得3x2+2x+3=0,这里a=3,b=2,c=3.
2. [2021临沂中考]方程x2-x=56的根是 ( )A.x1=7,x2=8B.x1=7,x2=-8C.x1=-7,x2=8D.x1=-7,x2=-8
3.3x2-5x+1=0 根据题意得,a=3,b=-5,c=1,所以该一元二次方程是3x2-5x+1=0.
4. 方程x2=2x+3的解为 .
5. [2021枣庄三十九中月考]若一个矩形的长和宽是方程x2-7x+8=0的两根,则该矩形的长为 .
6. 已知关于x的方程x2+3mx+m2=0的一个根是1,则m= .
9. 教材P46复习题T12变式已知关于x的一元二次方程(k-1)x2-k2x-1=0的一个根是-1,求k的值.方程是否还有其他根?若有,请求出来.
2. 一元二次方程2x2-2x-1=0的较大实数根在 ( )A.3和4之间B.2和3之间C.1和2之间D.0和1之间
5. [2021雅安中考改编]若直角三角形的两边长分别是方程x2-7x+12=0的两根,则该直角三角形的面积是 .
6. [2020随州中考]将关于x的一元二次方程x2-px+q=0变形为x2=px-q,就可以将x2表示为关于x的一次多项式,从而达到“降次”的目的,又如x3=x·x2=x(px-q)=…,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知x2-x-1=0且x>0,则x4-2x3+3x的值为 .
课时5 一元二次方程根的判别式
1. 一元二次方程x2-2x=0的根的判别式的值是 ( ) A.8B.4C.2D.0
知识点1 一元二次方程根的判别式
1.B 因为a=1,b=-2,c=0,所以b2-4ac=(-2)2-4×1×0=4.
2. 已知关于x的方程2x2+mx+1=0的根的判别式Δ=16,则m的值为 .
3. 原创题 一元二次方程x(x+4)+3=0的根的情况是 ( )A.有两个相等的实数根B.有两个不相等的实数根C.无实数根D.无法确定
知识点2 利用根的判别式判断一元二次方程根的情况
3.B 将x(x+4)+3=0整理,得x2+4x+3=0,则Δ=42-4×1×3=4>0,故方程x(x+4)+3=0有两个不相等的实数根.
4. [2021烟台中考]已知关于x的一元二次方程x2-mnx+m+n=0,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是 ( )A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定
4.A 由题中数轴,得m>0,n<0,m+n<0,∴mn<0,-4(m+n)>0,∴Δ=(-mn)2-4(m+n)>0,∴方程有两个不相等的实数根.
5. [2022西安期中]给出下列方程:① x2+1=2x;② x2+1=0;③ x2-2x=3;④ x2-2x=0.其中有两个相等实数根的是 .(填序号)
知识点3 利用根的判别式确定字母的值(取值范围)
9. 已知一元二次方程x2-kx+4=0有两个相等的实数根,则k的值为 .
9.±4 ∵一元二次方程x2-kx+4=0有两个相等的实数根,∴Δ=(-k)2-4×1×4=0,解得k=±4.
11. [2022延安期中]关于x的方程x2-2x+2m-1=0有实数根,且m为正整数,求m的值及此时方程的根.
11.解:∵关于x的方程x2-2x+2m-1=0有实数根,∴Δ=(-2)2-4(2m-1)≥0,解得m≤1.又∵m为正整数,∴m=1,则原方程为x2-2x+1=0,解得x1=x2=1.
2. [2021邵阳中考]在平面直角坐标系中,若直线y=-x+m不经过第一象限,则关于x的方程mx2+x+1=0的实数根的个数为( )A.0个 B.1个C.2个 D.1或2个
2.D 由直线y=-x+m不经过第一象限可知m≤0.当m=0时,原方程为x+1=0,解得x=-1,即原方程有1个实数根.当m<0时,mx2+x+1=0为关于x的一元二次方程,Δ=1-4m.∵m<0,∴1-4m>0,∴原方程有2个不相等的实数根.综上所述,关于x的方程mx2+x+1=0的实数根的个数为1或2个.
3. [2022唐山期中]小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2,则原方程的根的情况是 ( )A.不存在实数根B.有两个不相等的实数根C.有一个根是x=-1D.有两个相等的实数根
3.A 由题意,得当a=1,b=4时,一元二次方程为x2+4x+c=0,此时一个根为x=-1.将x=-1代入x2+4x+c=0,得(-1)2+4×(-1)+c=0,解得c=3.由于所抄的c比原方程的c值小2,所以原方程的c为5,所以原方程为x2+4x+5=0.因为Δ=42-4×1×5=-4<0,所以原方程不存在实数根.
4. 定义:当关于x的一元二次方程ax2+bx+c=0满足4a-2b+c=0时,称此方程为“蝴蝶”方程.若“蝴蝶”方程mx2+nx+p=0有两个相等的实数根,则下列等式正确的是 ( )A.m=4n=4pB.m=n=4pC.m=4n=pD.4m=n=p
5. 已知关于x的一元二次方程x2-6x+m=0有实数根,则m的最大整数值是 .
5.9 由题意,得Δ=(-6)2-4×1×m≥0,解得m≤9,所以m的最大整数值为9.
6. [2021南京鼓楼区期中]若方程x2+mx+1=0和x2+x+m=0有公共根,则常数m的值是 .
6.-2 设方程x2+mx+1=0和x2+x+m=0的公共根为t,则t2+mt+1=0 ①,t2+t+m=0 ②,①-②得(m-1)t=m-1.如果m=1,那么两个方程均为x2+x+1=0,Δ=12-4×1×1=-3<0,不符合题意;如果m≠1,那么t=1,把t=1代入①,得1+m+1=0,解得m=-2.故常数m的值为-2.
7. 已知关于x的一元二次方程mx2+nx-2=0.(1)当m=-2时,若方程的一个根为2,则n= ,另一个根为 . (2)当n=m-2时,方程根的情况是( )A.有两个不相等的实数根B.有两个相等的实数根C.有两个实数根D.不存在实数根(3)若方程的两个相等的实数根都是整数,请写出一组满足条件的m,n的值,并求此时方程的根.
8. 教材P36习题T9变式 已知关于x的方程mx2+(3m+1)x+3=0.(1)求证:不论m为何实数,此方程总有实数根.(2)若方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,求m的值.
8.解:(1)已知关于x的方程mx2+(3m+1)x+3=0,当m=0时,方程变形为x+3=0,解得x=-3;当m≠0时,Δ=(3m+1)2-4m·3=9m2-6m+1=(3m-1)2,∵(3m-1)2≥0,∴Δ≥0,∴此方程有两个实数根.综上,不论m为何实数,此方程总有实数根.
课时6 一元二次方程的根与系数的关系
1. [2021盐城中考]设x1,x2是一元二次方程x2-2x-3=0的两个根,则x1+x2的值为( ) A.-2B.-3C.2D.3
知识点1 一元二次方程的根与系数的关系
2. [2020泰州中考]方程x2+2x-3=0的两根为x1,x2,则x1·x2的值为 .
4. 一题多解[2022芜湖期中]已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是 ( )A.-7B.7C.3D.-3
知识点2 一元二次方程的根与系数的关系的应用
4.A 解法一 设另一个根为x,则x+2=-5,解得x=-7.解法二 把x=2代入x2+5x-m=0,得22+5×2-m=0,∴m=14,∴原方程即x2+5x-14=0,解得x=2或x=-7,∴另一个根是-7.
5. 已知一元二次方程x2+bx+c=0的两根分别为2和3,则b,c的值分别为 ( )A.5,6B.-5,-6C.5,-6D.-5,6
5.D ∵一元二次方程x2+bx+c=0的两根分别为2和3,∴2+3=-b,2×3=c,∴b=-5,c=6.
6. [2021遵义中考]在解关于x的一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根分别是-3,1.小明看错了一次项系数p,得到方程的两个根分别是5,-4,则原来的方程是 ( )A.x2+2x-3=0B.x2+2x-20=0C.x2-2x-20=0D.x2-2x-3=0
6.B 设方程x2+px+q=0的两个根分别为α,β.根据题意,得α+β=-p=-2,α·β=q=-20,所以p=2,则以α,β为根的一元二次方程是x2+2x-20=0.
7. [2020南京中考]关于x的方程(x-1)(x+2)=p2(p为常数)的根的情况,下列结论中正确的是 ( )A.两个正根 B.两个负根C.一个正根,一个负根D.无实数根
7.C 整理方程,得x2+x-2-p2=0,Δ=12-4×1×(-2-p2)=9+4p2>0,故该方程有两个不相等的实数根,设为x1,x2.∵x1·x2=-2-p2<0,∴x1,x2异号,∴该方程有一个正根,一个负根.
11.解:(1)根据题意得,Δ=(-6)2-4(2m-1)≥0,解得m≤5.∵x1+x2=6,x1x2=2m-1,x1=1,∴1+x2=6,x2=2m-1,∴x2=5,m=3.
专项1 一元二次方程最优解法的选用
(2)6(x-1)2-54=0,移项,得6(x-1)2=54,方程两边同时除以6,得(x-1)2=9,直接开平方,得x-1=3或x-1=-3,解得x1=4,x2=-2.
2. 解下列方程:(1)(2x+1)2-x2=0;(2)x(x+3)=2x+6.
(2)方程x(x+3)=2x+6可变形为x(x+3)=2(x+3),移项,得x(x+3)-2(x+3)=0,方程左边分解因式,得(x-2)(x+3)=0,所以x-2=0或x+3=0,得x1=2,x2=-3.
3. 解下列方程:(1)x2-4x+3=0; (2)x2-2x=24.
3.解:(1)x2-4x+3=0,移项,得x2-4x=-3,配方,得(x-2)2=1,直接开平方,得x-2=±1,所以x=2±1,即x1=3,x2=1.(2)x2-2x=24,配方,得x2-2x+1=25,即(x-1)2=25,直接开平方,得x-1=±5,所以x=1±5,即x1=6,x2=-4.
类型5 换元法解一元二次方程
专项2 根的判别式与其他知识的综合
1. [2021凉山州中考]函数y=kx+b的图象如图所示,则关于x的一元二次方程x2+bx+k-1=0的根的情况是 ( )A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.无法确定
类型1 与一次函数的综合
1.C 根据题图可得k<0,b<0,所以b2>0,-4k>0.因为Δ=b2-4(k-1)=b2-4k+4>0,所以方程有两个不相等的实数根.
2. 一次函数y=kx+b(k≠0)的图象如图所示,在第一象限内的图象上是否存在一点P,使过点P所作的两坐标轴的垂线与两坐标轴围成的四边形的面积为2?若存在,求出点P的坐标;若不存在,请说明理由.
2.解:不存在.理由如下:如图,设直线y=kx+b(k≠0)交x轴于点A,交y轴于点B,过点P作PE⊥x轴于点E,PF⊥y轴于点F.
3. [2022天门期中]已知m,n,4分别是等腰三角形(非等边三角形)三边的长,且m,n是关于x的一元二次方程x2-6x+k+2=0的两个根,则k的值等于 ( )A.7B.7或6C.6或-7 D.6
类型2 与三角形的综合
3.B ∵m,n,4分别是等腰三角形(非等边三角形)三边的长,∴当m=4(或n=4)时,一元二次方程x2-6x+k+2=0的一个根为4,∴42-6×4+k+2=0,解得k=6;当m=n≠4时,Δ=(-6)2-4×(k+2)=0,解得k=7.综上所述,k的值等于6或7.
(2)由(1)知a=b,所以方程x2+mx-3m=0有两个相等的实数根,所以Δ=m2-4×1×(-3m)=m2+12m=0,所以m2=-12m.因为a,b为正数,所以m≠0.将m2=-12m两边同时除以m,得m=-12.
5. [2022北京朝阳区调研]如图,在△ABC中,∠A=90°,AB=12 cm,AC=8 cm,现有动点P从点B出发,沿射线BA运动,动点Q从点C出发,沿射线CA运动,已知点P的速度是2 cm/s,点Q的速度是1 cm/s,它们同时出发,设运动时间是t s(t>0).(1)当t=4时,求△APQ的面积.(2)多少秒时,△APQ的面积是△ABC面积的一半?
1. [2021毕节中考]已知关于x的一元二次方程ax2-4x-1=0有两个不相等的实数根,则a的取值范围是 ( ) A.a≥-4 B.a>-4C.a≥-4且a≠0D.a>-4且a≠0
易错点1 忽视二次项系数不为0
1.D 根据题意得,a≠0且Δ=(-4)2-4a×(-1)>0,解得a>-4且a≠0.
变式1 [2020武威中考]已知x=1是一元二次方程(m-2)x2+4x-m2=0的一个根,则m的值为 ( )A.-1或2B.-1C.2D.0
变式1B 把x=1代入(m-2)x2+4x-m2=0,得m-2+4-m2=0,即-m2+m+2=0,解得m1=2,m2=-1.∵(m-2)x2+4x-m2=0是关于x的一元二次方程,∴m-2≠0,∴m≠2,∴m=-1.
2. [2020天门中考]关于x的方程x2+2(m-1)x+m2-m=0有两个实数根α,β,且α2+β2=12,那么m的值为 ( )A.-1B.-4C.-4或1D.-1或4
易错点2 忽视方程有实数根的隐含条件:Δ≥0
2.A ∵关于x的方程x2+2(m-1)x+m2-m=0有两个实数根,∴Δ=[2(m-1)]2-4×1×(m2-m)=-4m+4≥0,解得m≤1.∵关于x的方程x2+2(m-1)x+m2-m=0有两个实数根α,β,∴α+β=-2(m-1),αβ=m2-m,∴α2+β2=(α+β)2-2αβ=[-2(m-1)]2-2(m2-m)=12,即m2-3m-4=0,解得m=-1或m=4(舍去).
易错点3 解一元二次方程时的常见问题
1. [2021济宁中考]已知m,n是一元二次方程x2+x-2 021=0的两个实数根,则代数式m2+2m+n的值等于 ( ) A.2 019B.2 020C.2 021D.2 022
疑难点1 整体思想的应用
1.B 根据题意可知m2+m-2 021=0,∴m2+m=2 021.由一元二次方程根与系数的关系,得m+n=-1,故m2+2m+n=(m2+m)+(m+n)=2 021-1=2 020.
3. [2022广州期中]若m是方程x2+x-1=0的根,则式子m3+2m2+2 022的值为 ( )A.2 023 B.2 022C.2 021 D.2 020
3.A ∵m是方程x2+x-1=0的根,∴m2+m=1,∴m3+2m2+2 022=m3+m2+m2+2 022=m(m2+m)+m2+2 022=m+m2+2 022=1+2 022=2 023.
5. 已知关于x的方程x2-2(m+1)x+m2+2=0.(1)若方程总有两个实数根,求m的取值范围;(2)若两实数根x1,x2满足(x1+1)(x2+1)=8,求m的值.
疑难点2 配方法的应用
课时1 实践与探索(1)
知识点1 图形面积问题
3. 手卷是国画装裱中横幅的一种体式,以能握在手中顺序展开阅览得名,它主要由“引首”“画心”“拖尾”三部分组成(这三部分都是矩形形状),分隔这三部分的其余部分统称为“隔水”.下图中手卷长1 000 cm,宽40 cm,引首和拖尾完全相同,其宽度都为100 cm.若隔水的宽度为x cm,画心的面积为15 200 cm2,求x的值.
3.解:根据题意,得(1 000-4x-200)(40-2x)=15 200,解得x1=210(不合题意,舍去),x2=10,所以x的值为10.
4. [2022上海金山区期中]某纸箱厂要生产一批无盖纸盒,购进了长为20 cm、宽为16 cm的长方形硬纸板,将硬纸板的四个角剪掉四个小正方形(如图),剩下的部分正好做成无盖纸盒(不计损耗).若纸盒的底面面积为140 cm2,则剪下的小正方形的边长是多少厘米?
4.解:设剪下的小正方形的边长是x cm,则做成的无盖纸盒的底面长为(20-2x)cm、宽为(16-2x) cm.依题意,得(20-2x)(16-2x)=140,整理得x2-18x+45=0,解得x1=3,x2=15.∵16-2x>0,∴x<8,∴x=3.答:剪下的小正方形的边长是3 cm.
5. [2022德州期中]如图,用长为24 m的篱笆,一面利用墙(墙的最大可用长度为10 m)围成中间有一道篱笆的长方形花圃.(1)现要围成面积为45 m2的花圃,则AB的长是多少?(2)小华想围成面积为48 m2的花圃,你认为他的想法能实现吗?并说明理由.
5.解:(1) 设AB的长是x m,由题意得x(24-3x)=45,解得x1=3,x2=5.当x=3时,BC=24-3x=15(m),15>10(不符合题意,舍去);当x=5时,BC=24-3x=24-15=9(m),9<10(符合题意).答:AB的长是5 m.
(2)不能实现.理由如下:设AB的长是y m,由题意得y(24-3y)=48,解得y1=y2=4,当y=4时,BC=24-3y=12(m),12>10(不符合题意,舍去),所以不能围成面积为48 m2的花圃,小华的想法不能实现.
6. [2021福建中考]某市2018年底森林覆盖率为63%.为贯彻落实“绿水青山就是金山银山”的发展理念,该市大力开展植树造林活动,2020年底森林覆盖率达到68%.如果这两年森林覆盖率的年平均增长率为x,那么,符合题意的方程是 ( )(1+x)=(1+x)2=(1+2x)=(1+2x)2=0.68
知识点2 变化率问题
6.B 由题意,得2019年底森林覆盖率为0.63(1+x),2020年底森林覆盖率为0.63(1+x)2,由此可列方程为0.63(1+x)2=0.68.
7. [2021襄阳中考]随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5 000元,现在生产一吨药的成本是4 050元.设生产成本的年平均下降率为x,下面所列方程正确的是 ( )A.5 000(1+x)2=4 050B.4 050(1+x)2=5 000C.5 000(1-x)2=4 050D.4 050(1-x)2=5 000
8. 目前以5G等为代表的战略性新兴产业蓬勃发展.某市2020年底有5G用户2万户,计划到2022年底全市5G用户数累计达到8.72万户.设全市5G用户数年平均增长率为x,则x的值为 .
8.40%(或0.4) 2021年底全市5G用户数为2(1+x)万户,2022年底全市5G用户数为2(1+x)2万户,依题意,得2+2(1+x)+2(1+x)2=8.72,整理,得x2+3x-1.36=0,解得x1=0.4=40%,x2=-3.4(不合题意,舍去).
9. 教材P39问题2变式在国家积极研发和生产调配下,某种型号的医疗器械连续两年降价,第一年下降20%,第二年下降80%,那么该医疗器械这两年的平均降价率是 .
9.60% 设该医疗器械这两年的平均降价率是x,依题意,得(1-x)2=(1-20%)×(1-80%),解得x1=0.6,x2=1.4(不合题意,舍去),故该医疗器械这两年的平均降价率为60%.
10. [2021东营中考]“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1 008公斤的目标.(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1 200公斤,请通过计算说明他们的目标能否实现.
10.解:(1)设亩产量的平均增长率为x,根据题意,得700(1+x)2=1 008,解得x1=0.2=20%,x2=-2.2(舍去).答:亩产量的平均增长率为20%.(2)第四阶段的亩产量为1 008×(1+20%)=1 209.6(公斤).∵1 209.6>1 200,∴他们的目标能实现.
11. 原创题 某楼盘2022年1月份的均价为16 000元 /m2,受新型冠状病毒肺炎疫情的影响,开发商连续两个月下调房价,3月份的均价为14 440元/m2.(1)求该楼盘的均价在2022年1月到3月期间的月平均下降率;(2)王叔叔决定等到均价低于14 000元/m2时买房子,按这样的月平均下降率,王叔叔能在2022年4月份买房子吗?
11.解:(1)设该楼盘2022年1月到3月期间均价的月平均下降率为x,根据题意,得16 000(1-x)2=14 440,解得x=0.05或x=1.95(不合题意,舍去).答:该楼盘2022年1月到3月期间均价的月平均下降率为5%.(2)2022年4月份的均价为14 440×(1-0.05)=13 718(元/m2),13 718<14 000,故王叔叔能在2022年4月份买房子.
1. [2022德阳期中]如图,在宽为20 m,长为32 m的长方形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540 m2,求道路的宽.设道路的宽为x m,则可列方程为 ( )A.(20-x)(32-x)=540B.(20-x)(32-x)=100C.(20+x)(32-x)=540D.(20+x)(32-x)=100
1.A 由题意可将道路平移如图所示,余下的部分种上草坪,则草坪面积为空白长方形面积,空白长方形的长为(32-x)m,宽为(20-x)m,故可列方程为(20-x)(32-x)=540.
2. 如图是由三个边长分别为4,6,x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 .
2.2或4 如图,∵直线AB平分原图形以及矩形ACBD的对角线AB平分矩形ACBD,∴x(6-x)=2×4,解得x=2或x=4.
3. [2020山西中考]如图是一张长12 cm、宽10 cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24 cm2的有盖的长方体铁盒,则剪去的正方形的边长为 cm.
4. 2022年1月,某市肉类批发市场猪肉价格猛涨,原来单价为16元/千克的猪肉,经过1月和2月连续两个月上升后,物价部门紧急出台相关政策控制价格,3月猪肉价格下降了36%,恰好与涨价前的价格相同,则1月、2月猪肉价格的平均增长率为 .
4.25% 设该市2022年1月、2月猪肉价格的平均增长率为x,根据题意,得16(1+x)2(1-36%)=16,解得 x=0.25或x=-2.25(舍去),所以1月、2月猪肉价格的平均增长率为25%.
5. [2021淄博中考]为更好地发展低碳经济,建设美丽中国.某公司对其生产设备进行了升级改造,不仅提高了产能,而且大幅降低了碳排放量.已知该公司去年第三季度产值是2 300万元,今年第一季度产值是3 200万元,假设公司每个季度产值的平均增长率相同. (1)求该公司每个季度产值的平均增长率;(2)该公司今年总产值能否超过1.6亿元?并说明理由.
5.解:(1)设该公司每个季度产值的平均增长率为x,依题意,得2 300(1+x)2=3 200,解得x1=0.18=18%,x2=-2.18(不合题意,舍去).答:该公司每个季度产值的平均增长率为18%.(2)能.理由如下:3 200+3 200×(1+18%)+3 200×(1+18%)2+3 200×(1+18%)3=3 200+3 200×1.18+3 200×1.39+3 200×1.64=3 200+3 776+4 448+5 248=16 672,1.6亿元=16 000万元,∵16 672>16 000,∴该公司今年总产值能超过1.6亿元.
素养提升6. 结论开放要在一块长16 m、宽12 m的长方形荒地上建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗?若不符合,请帮小芳计算出小路的宽度均为多少米.(2)你还有其他的设计方案吗?请在图3中画出你所设计的草图,并将花园部分涂上阴影.
课时2 实践与探索(2)
1. [2022无锡调研]某种花卉每盆的盈利与每盆的株数有一定的关系.每盆种植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元.要使每盆的盈利达到15元,每盆应多种植多少株?设每盆多种植x(0≤x<8)株,则可以列出的方程是 ( ) A.(3+x)(4-0.5x)=15B.(3+x)(4+0.5x)=15C.(x+4)(3-0.5x)=15D.(x+1)(4-0.5x)=15
知识点1 销售问题
1.A 若每盆多种植x株,则每盆有(3+x)株.因为每盆增加1株,平均每株盈利减少0.5元,所以多种植x株后每株盈利会减少0.5x元,即多种植x株后每株的盈利为(4-0.5x)元.要使每盆的盈利达到15元,则(3+x)(4-0.5x)=15.
2. 一种商品的进价为5元/件,市场调查发现:当售价为m元/件时,每天可销售该商品(m+5)件,此时获利144元.则该商品的售价为 元/件.
2.13 由题意,得(m-5)(m+5)=144,解得m1=13,m2=-13(不符合题意,舍去),所以该商品的售价为13元/件.
3. [2021菏泽中考]列方程(组)解应用题端午节期间,某水果超市调查某种水果的销售情况.下面是调查员的对话:小王:该水果的进价是每千克22元.小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.根据他们的对话,解决下面所给问题:超市每天要获得销售利润3 640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元.
4. 教材P43习题T5变式[2021烟台中考]直播购物逐渐走进了人们的生活.某电商在某音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
5. 教材P36习题T6变式两个连续偶数的积为288,设其中较小的一个偶数为x,可得方程为 .
5.x(x+2)=288
6. [2021山西中考]2021年7月1日是建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数.(请用方程知识解答)
6.解:设这个最小数为x.根据题意,得x(x+8)=65,解得x1=5,x2=-13(不符合题意,舍去).答:这个最小数为5.
7. [2022福州模拟]子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·第二章·为政篇》列方程解决下面问题:大江东去浪淘尽,千古风流数人物;而立之年督东吴,早逝英年两位数;十位恰小个位三,个位平方与寿符;哪位学子算得快,多少年华属周瑜?
7.解:设周瑜逝世年龄的个位数字为x,则十位数字为x-3,根据题意,得10(x-3)+x=x2,解得x1=5,x2=6.当x=5时,周瑜的年龄是25岁,因为25不是而立之年,所以不符合题意,舍去;当x=6时,周瑜的年龄是36岁,符合题意.答:周瑜的年龄是36岁.
9. 汽车在行驶过程中由于惯性作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为刹车距离.在一个限速为35 km/h的弯道上,甲、乙两车相向而行,发现情况不对时,同时刹车,但还是相撞了,事后测得甲车的刹车距离为12 m,乙车的刹车距离为10 m.已知甲车的刹车距离s甲(m)与车速x(km/h)之间的关系是s甲=0.01x2+0.1x,乙车的刹车距离s乙(m)与车速y(km/h)之间的关系是s乙=0.005y2+0.05y,请你从两车的速度方面分析事故原因.
9.解:甲车的刹车距离为12 m,由0.01x2+0.1x=12,即x2+10x-1 200=0,解得x1=30,x2=-40(不合题意,舍去),所以甲车的速度为30 km/h,不超过限速.乙车的刹车距离为10 m,由0.005y2+0.05y=10,即y2+10y-2 000=0,解得y1=40,y2=-50(不合题意,舍去),所以乙车的速度为40 km/h,超过了限速.综上,事故原因为乙车超速.
1. 一个两位数个位上的数字比十位上的数字大1,个位上的数字与十位上的数字的平方和为13,则这个两位数为 ( ) A.32D.14
1.B 设这个两位数十位上的数字为x,则个位上的数字为x+1,由题意,得x2+(x+1)2=13,解得x1=2,x2=-3(舍去),所以这个两位数十位上的数字为2,个位上的数字为3,所以这个两位数为23.
2. 一个农业合作社以64 000元的成本收购了某种农产品80吨,目前可以以1 200元/吨的价格售出,如果储藏起来,每星期会损失2吨,且每星期需支付各种费用1 600元,但同时每星期每吨的价格将上涨200元.那么储藏 个星期再出售这批农产品可获利122 000元.
2.15 设储藏x个星期再出售这批农产品可获利122 000元,由题意得(1 200+200x)×(80-2x)-1 600x-64 000=122 000,化简,得x2-30x+225=0,解得x1=x2=15.故储藏15个星期再出售这批农产品可获利122 000元.
课时3 实践与探索(3)
1. [2021龙东地区中考]有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是 ( ) A.14B.11C.10D.9
1.B 设每轮传染中平均一个人传染x人,由题意,知1+x+x(1+x)=144,可得(1+x)2=144,解得x1=11,x2=-13(舍去).
2. [2022保定期末]八年级学生小程观看了《开学第一课》后,写了一份《奋斗吧,少年》的倡议书,在微信朋友圈传播.传播规则:将该倡议书发表在自己的微信朋友圈上,再邀请n个好友转发该倡议书,每个好友转发该倡议书之后,又邀请n个互不相同的好友转发该倡议书.若共有421人参与了该倡议书的传播活动,则n= .
2.20 由题意可知1+n+n2=421,解得n1=20,n2=-21(舍去),所以n=20.
3. 某种电脑病毒的传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
3.解:设每轮感染中平均一台电脑会感染x台电脑,依题意,得1+x+x(x+1)=81,即(x+1)2=81,解得x1=8,x2=-10(舍去).(x+1)3=(8+1)3=729>700.答:每轮感染中平均一台电脑会感染8台电脑.若病毒得不到有效控制,3轮感染后,被感染的电脑会超过700台.
4. [2021毕节中考]某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为 ( )A.5B.6C.7D.8
知识点2 单、双循环问题
5. 在学校举行的图书共享仪式上同学们互赠图书,每名同学都把自己的图书向本组其他成员赠送一本,某组共互赠了156本图书,则该组一共有 名同学.
5.13 设该组一共有x名同学,根据题意,得x(x-1)=156,解得x=-12(舍去)或x=13,所以这个组一共有13名同学.
6. 第四届数字中国建设峰会于2021年4月25日在福州开幕,在其中一场数字产品的交易碰头会上,与会的每两家公司之间都签订了一份互助协议,所有公司共签订了210份协议,共有多少家公司参加这场交易碰头会?
7. 《李白饮酒》数谜诗——李白每天不离酒,三餐依次增一斗;三餐斗数两两乘,乘积相加一四六;要知酒仙量如何,求出每餐饮几斗.则早餐饮 斗.
7.6 设早餐饮酒x斗,则午餐饮酒(x+1)斗,晚餐饮酒(x+2)斗,根据题意,得x(x+1)+(x+1)(x+2)+x(x+2)=146,解得x1=6,x2=-8(不合题意,舍去).
8. [2021沈阳中考]某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行、列数相同,增加了多少行或多少列?
8.解:设增加了x行,则增加的列数为x.根据题意,得(6+x)(8+x)-6×8=51,整理,得x2+14x-51=0,解得x1=3,x2=-17(舍去).答:增加了3行3列.
1. [2022江门期末]某植物的一根主干长出若干数目的支干,每个支干又长出同样数目的小分支.若主干、支干、小分支共有91支,由每个支干长出的小分支数目为 ( ) A.10 B.9C.10或9 D.-10或9
1.B 设每个支干长出的小分支为x支,由题意,得1+x+x2=91,解得x1=9,x2=-10(舍去).
2. 在一次数学兴趣小组活动中,每两名学生握手一次,但小明因中途有事离开,他记得有3人没有和他握过手,经统计所有握手共42次,则参加活动的学生有 ( )A.7人B.8人C.9人D.10人
3. [2021营口期末]某居委会3人同时得知一则喜讯,经过两轮传递使得有864人的居民小区知晓率达50%,则每轮传递中平均一人传递的人数为 .
3.11 设每轮传递中平均一人传递了x人,由题意,得3+3x+(3+3x)x=864×50%,整理,得(1+x)2=144,解得x1=11,x2=-13(舍去),所以每轮传递中平均一人传递了11人.
4. 在一次象棋比赛中,实行单循环赛制(每个选手都与其他选手比赛一局),每局赢者记2分,输者记0分,如果平局,两个选手各记1分.今有4个同学统计了比赛中全部选手的得分总和,结果分别为2 025分、2 024 分、2 070分、2 028分,经核实只有一位同学统计无误,这次比赛中共有多少名选手参赛?
2. 形如x2-(1+n)x+n=0的一元二次方程的解的规律探究根据要求,解答下列问题.(1)解下列方程(直接写出方程的解即可):①方程x2-2x+1=0的解为 ; ②方程x2-3x+2=0的解为 ; ③方程x2-4x+3=0的解为 ; ……(2)根据以上方程及其解的特征,请猜想:①方程x2-9x+8=0的解为 ; ②关于x的方程 的解为x1=1,x2=n. (3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
2. [2021海南中考]用配方法解方程x2-6x+5=0,配方后所得的方程是 ( )A.(x+3)2=-4B.(x-3)2=-4C.(x+3)2=4D.(x-3)2=4
2.D x2-6x+5=0,移项,得x2-6x=-5,配方,得x2-6x+9=-5+9,即(x-3)2=4.
3. [2021滨州中考]下列一元二次方程中,无实数根的是 ( )A.x2-2x-3=0B.x2+3x+2=0C.x2-2x+1=0D.x2+2x+3=0
5. 结论开放[2021广东中考]若一元二次方程x2+bx+c=0(b,c为常数)的两根x1,x2满足-3
6. [2020济南中考]如图,在一块长15 m、宽10 m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种花草,要使绿化面积为126 m2,则修建的路宽应为 m.
6.1 设道路的宽为x m,根据题意得(10-x)(15-x)=126,解得x1=1,x2=24(不合题意,舍去),则道路的宽应为1 m.
7. [2021徐州中考]解方程:x2-4x-5=0.
7.解:x2-4x-5=0,移项,得x2-4x=5,配方,得x2-4x+4=5+4,即(x-2)2=9,直接开平方,得x-2=±3,所以x1=5,x2=-1.
8. 一题多解[2021北京中考]已知关于x的一元二次方程x2-4mx+3m2=0.(1)求证:该方程总有两个实数根;(2)若m>0,且该方程的两个实数根的差为2,求m的值.
8.(1)证明:x2-4mx+3m2=0,∵Δ=(-4m)2-4×1×3m2=4m2≥0,∴该方程总有两个实数根.
(2)解:解法一 由公式法解关于x的一元二次方程x2-4mx+3m2=0,可得x1=3m,x2=m.∵m>0,∴3m-m=2,∴m=1.解法二 设方程的两根分别为x1,x2,则x1+x2=4m,x1·x2=3m2.∵x1-x2=2,∴(x1-x2)2=4,∴(x1+x2)2-4x1x2=4,∴(4m)2-4×3m2=4,∴m=±1.又∵m>0,∴m=1.
9. [2021日照中考]某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量y(桶)与每桶降价x(元)(0
1.D 将方程变为一般形式为5x2+1=0,一次项系数为0.
2. 用配方法解方程x2-6x-8=0时,配方结果正确的是 ( )A.(x-3)2=17B.(x-3)2=14C.(x-6)2=44D.(x-3)2=1
3. 若x=1是关于x的一元二次方程x2+ax+2b=0的解,则2a+4b= ( )A.-2B.-3C.-1D.-6
3.A 由题意,得1+a+2b=0,所以a+2b=-1,所以2a+4b=2(a+2b)=2×(-1)=-2.
4. [2022平凉期中]若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为( )A.16 或24 D.48
4.B ∵四边形ABCD是菱形,∴AB=BC=CD=AD.由x2-10x+24=0,解得x=4或x=6.假设BD=8,分两种情况:①当AB=AD=4时,4+4=8,不能构成三角形;②当AB=AD=6时,6+6>8,能构成三角形.故该菱形ABCD的周长=4AB=24.
8. [2022宁德期中]已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是 ( )A.1一定不是关于x的一元二次方程x2+bx+a=0的根B.0一定不是关于x的一元二次方程x2+bx+a=0的根C.1和-1都是关于x的一元二次方程x2+bx+a=0的根D.1和-1不都是关于x的一元二次方程x2+bx+a=0的根
二、填空题9. 已知关于x的方程(m-1)x|m|+1-x-2 021=0是一元二次方程,则m的值为 .
10. [2022黄冈模拟]一个两位数,十位上的数字比个位上的数字的平方小3,如果把这个数的个位数字与十位数字交换,那么所得到的两位数比原来的数小27,则原来的两位数是 .
12. [2020黑龙江大庆中考]已知关于x的一元二次方程x2-2x-a=0,有下列结论:①当a>-1时,方程有两个不相等的实数根;②当a>0时,方程不可能有两个异号的实数根;③当a>-1时,方程的两个实数根不可能都小于1;④当a>3时,方程的两个实数根一个大于3,另一个小于3.以上4个结论中,正确的个数为 .
三、解答题13. 解下列方程:(1)(x-3)(x-1)=3;(2)(2x-1)2-121=0;(3)x2-2x-3=0;(4)2x2-5x+3=0.
13.解:(1)(x-3)(x-1)=3可化为x2-4x=0,即x(x-4)=0,∴x1=0,x2=4.(2)(2x-1)2-121=0可以变形为(2x-1)2=121,直接开平方,得2x-1=±11,∴x1=6,x2=-5.
14. 一题多解已知关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根.(1)求k的取值范围;(2)若k为正整数,且该方程的根都是整数,求方程的根.
湘教版九年级上册2.1 一元二次方程作业课件ppt: 这是一份湘教版九年级上册2.1 一元二次方程作业课件ppt,共22页。
华师大版九年级上册23.5 位似图形作业课件ppt: 这是一份华师大版九年级上册23.5 位似图形作业课件ppt,共20页。
初中数学华师大版九年级上册23.4 中位线作业ppt课件: 这是一份初中数学华师大版九年级上册23.4 中位线作业ppt课件,共34页。













