





还剩7页未读,
继续阅读
所属成套资源:新版华东师大版九年级数学下册全一册作业课件
成套系列资料,整套一键下载
2023九年级数学下册第27章圆专项3求圆中阴影部分面积的常用方法作业课件新版华东师大版
展开
这是一份2023九年级数学下册第27章圆专项3求圆中阴影部分面积的常用方法作业课件新版华东师大版,共14页。
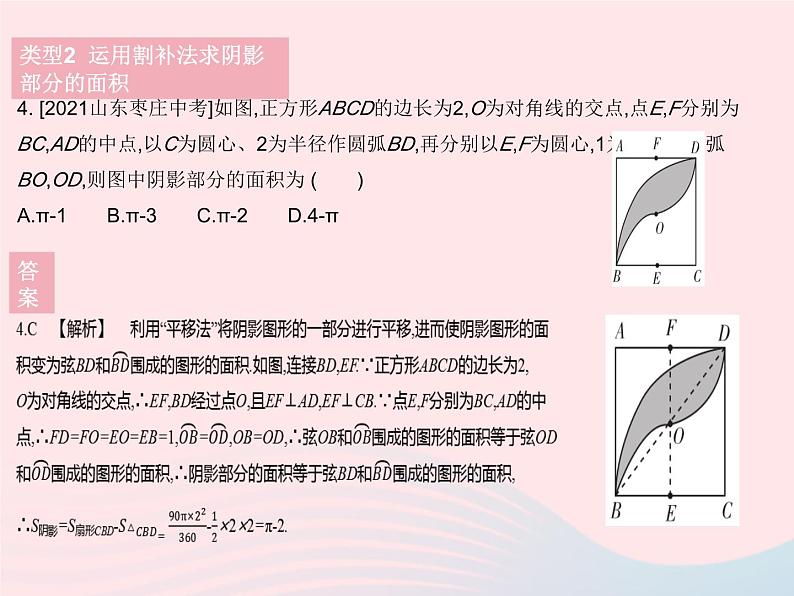
专项3 求圆中阴影部分面积的常用方法类型1 直接运用规则图形面积的和、差求阴影部分的面积 答案类型1 直接运用规则图形面积的和、差求阴影部分的面积 答案类型1 直接运用规则图形面积的和、差求阴影部分的面积3. [2020重庆中考A卷]如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分面积为 .(结果保留π) 答案类型2 运用割补法求阴影部分的面积4. [2021山东枣庄中考]如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点,以C为圆心、2为半径作圆弧BD,再分别以E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为 ( )A.π-1 B.π-3 C.π-2 D.4-π 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积2.利用同(等)底等高的三角形进行等积替换6. 如图,AC与BD是☉O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10 cm,∠BAC=36°,则图中阴影部分的面积为( )A.5π cm2 B.10π cm2 C.15π cm2 D.20π cm2 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积 9.【解析】 (1)∵四边形ABCD为正方形,∴AB=BC=AD=2,∠ABC=90°. ∵将△BEC绕点B逆时针旋转90°得到△BFA,∴△BFA≌△BEC,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,∴∠AFB+∠FAB=90°.∵将线段FA绕点F顺时针旋转90°得到线段FG.∴∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG.∵AF=EC,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG.答案
专项3 求圆中阴影部分面积的常用方法类型1 直接运用规则图形面积的和、差求阴影部分的面积 答案类型1 直接运用规则图形面积的和、差求阴影部分的面积 答案类型1 直接运用规则图形面积的和、差求阴影部分的面积3. [2020重庆中考A卷]如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分面积为 .(结果保留π) 答案类型2 运用割补法求阴影部分的面积4. [2021山东枣庄中考]如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点,以C为圆心、2为半径作圆弧BD,再分别以E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为 ( )A.π-1 B.π-3 C.π-2 D.4-π 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积2.利用同(等)底等高的三角形进行等积替换6. 如图,AC与BD是☉O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10 cm,∠BAC=36°,则图中阴影部分的面积为( )A.5π cm2 B.10π cm2 C.15π cm2 D.20π cm2 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积 答案类型3 利用等积法求阴影部分的面积 9.【解析】 (1)∵四边形ABCD为正方形,∴AB=BC=AD=2,∠ABC=90°. ∵将△BEC绕点B逆时针旋转90°得到△BFA,∴△BFA≌△BEC,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,∴∠AFB+∠FAB=90°.∵将线段FA绕点F顺时针旋转90°得到线段FG.∴∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG.∵AF=EC,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG.答案
相关资料
更多









