


沪科版七年级上册3.5 三元一次方程组及其解法随堂练习题
展开
这是一份沪科版七年级上册3.5 三元一次方程组及其解法随堂练习题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
![]() 3.5三元一次方程及其解法同步练习-沪科版数学七年级上册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.以
3.5三元一次方程及其解法同步练习-沪科版数学七年级上册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.以![]() 为解建立三元一次方程组,不正确的是( )A.
为解建立三元一次方程组,不正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.若
2.若![]() ,则
,则![]() 等于( )A.
等于( )A.![]() B.
B.![]() C.2 D.
C.2 D.![]() 3.某宾馆有单人间,双人间,三人间三种客房供游客选择居住,现某旅游团有20名旅客同时安排游客居住在该宾馆,若每个房间都住满,共租了9间客房,则居住方案( )A.1种 B.2种 C.3种 D.4种4.三元一次方程组
3.某宾馆有单人间,双人间,三人间三种客房供游客选择居住,现某旅游团有20名旅客同时安排游客居住在该宾馆,若每个房间都住满,共租了9间客房,则居住方案( )A.1种 B.2种 C.3种 D.4种4.三元一次方程组 的解是( )A.
的解是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.三元一次方程组
5.三元一次方程组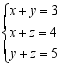 的解是 ( )A.
的解是 ( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.下列方程组中,是三元一次方程组的是( )A.
6.下列方程组中,是三元一次方程组的是( )A.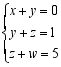 B.
B.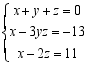 C.
C. D.
D.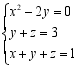 7.方程组
7.方程组 的解是( )A.
的解是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.解三元一次方程组
8.解三元一次方程组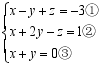 要使解法较为简便,首先应进行的变形为( )A.①+② B.①﹣② C.①+③ D.②﹣③9.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )
要使解法较为简便,首先应进行的变形为( )A.①+② B.①﹣② C.①+③ D.②﹣③9.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )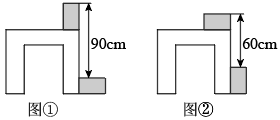 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.若
10.若![]() ,
,![]() ,则x+y+z的值等于( )A.0 B.2 C.1 D.无法求出 二、填空题11.疫情期间,为了降低外出感染风险,各大超市开通了送货到小区的便民服务.某超市推出A、B、C三种蔬菜,并将A、B、C三种蔬菜搭配、装袋,采用甲、乙、丙三种袋装进行销售.已知每袋的成本分别为袋中A、B、C三种蔬菜的成本之和,且袋子的成本忽略不计.每袋甲分别装A、B、C三种蔬菜3斤、1斤、1斤,每袋乙分别装A、B、C三种蔬菜1斤、2斤、2斤.每袋甲的总成本是每斤A成本的12倍,每袋甲的利润率为25%.每袋甲比每袋乙的售价低25%.每袋丙在成本上提高40%标价后打八折销售,每袋的获利为每斤A成本的1.2倍.当销售甲、乙、丙三种袋装蔬菜的数量之比为1:2:5时,则销售的总利润率为 .12.解三元一次方程组
,则x+y+z的值等于( )A.0 B.2 C.1 D.无法求出 二、填空题11.疫情期间,为了降低外出感染风险,各大超市开通了送货到小区的便民服务.某超市推出A、B、C三种蔬菜,并将A、B、C三种蔬菜搭配、装袋,采用甲、乙、丙三种袋装进行销售.已知每袋的成本分别为袋中A、B、C三种蔬菜的成本之和,且袋子的成本忽略不计.每袋甲分别装A、B、C三种蔬菜3斤、1斤、1斤,每袋乙分别装A、B、C三种蔬菜1斤、2斤、2斤.每袋甲的总成本是每斤A成本的12倍,每袋甲的利润率为25%.每袋甲比每袋乙的售价低25%.每袋丙在成本上提高40%标价后打八折销售,每袋的获利为每斤A成本的1.2倍.当销售甲、乙、丙三种袋装蔬菜的数量之比为1:2:5时,则销售的总利润率为 .12.解三元一次方程组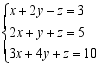 时,先消去z,得二元一次方程组
时,先消去z,得二元一次方程组![]() ,再消去y,得一元一次方程2x=3,解得x=
,再消去y,得一元一次方程2x=3,解得x=![]() ,从而得y= ,z= .13.分别写有数字2,0,
,从而得y= ,z= .13.分别写有数字2,0,![]() 的卡片若干张,从中随机抽取20张,将这20张卡片上的数字分别记为
的卡片若干张,从中随机抽取20张,将这20张卡片上的数字分别记为![]() ,满足
,满足![]() 且
且![]()
![]() ,则抽取写有数字
,则抽取写有数字![]() 的卡片有 张.14.由不同生产商提供
的卡片有 张.14.由不同生产商提供![]() 套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的
套校服参加比选,甲、乙、两三个同学分别参加比选,比选后结果是:每套校服至少有一人选中,且每人都选中了其中的![]() 套校服.如果将其中只有
套校服.如果将其中只有![]() 人选中的校服称作“不受欢迎校服”,
人选中的校服称作“不受欢迎校服”,![]() 人选中的校服称作“颇受欢迎校服”,
人选中的校服称作“颇受欢迎校服”,![]() 人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多 套. 15.北京冬奥会志愿者招募迎来全球申请热潮,赛会志愿者将在北京赛区、延庆赛区、张家口赛区的竞赛场馆开展志愿服务,北京赛区、延庆赛区、张家口赛区的志愿者人数之比为5∶3∶2.随着赛事的调整,各赛区的志愿者人数均要增加,其中等于其余两个赛区增加的总人数的
人都选中的校服称作“最受欢迎校服”,则“不受欢迎校服”比“最受欢迎校服”多 套. 15.北京冬奥会志愿者招募迎来全球申请热潮,赛会志愿者将在北京赛区、延庆赛区、张家口赛区的竞赛场馆开展志愿服务,北京赛区、延庆赛区、张家口赛区的志愿者人数之比为5∶3∶2.随着赛事的调整,各赛区的志愿者人数均要增加,其中等于其余两个赛区增加的总人数的![]() ,则增加后北京赛区志愿者人数占所有赛区增加后的总人数的
,则增加后北京赛区志愿者人数占所有赛区增加后的总人数的![]() .为使延庆赛区、张家口赛区增加后的志愿者人数之比为6∶5,则延庆赛区增加的志愿者人数与各赛区增加的志愿者总人数之比是 .16.利用两块大小相同的长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是 .
.为使延庆赛区、张家口赛区增加后的志愿者人数之比为6∶5,则延庆赛区增加的志愿者人数与各赛区增加的志愿者总人数之比是 .16.利用两块大小相同的长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是 .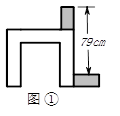
 17.甲、乙、丙、丁是四个不同平台的外卖员,每配送一单即可获得相应配送费且均为整数.已知乙每一单的配送费为甲的两倍,丁每一单的配送费为丙的两倍.12月第一周,甲、乙、丙的配送量之比为
17.甲、乙、丙、丁是四个不同平台的外卖员,每配送一单即可获得相应配送费且均为整数.已知乙每一单的配送费为甲的两倍,丁每一单的配送费为丙的两倍.12月第一周,甲、乙、丙的配送量之比为![]() ,丁的配送量为100单,且他们共获得配送费3700元.第二周配送量增加,甲增加的配送量占乙、丙配送量之和的
,丁的配送量为100单,且他们共获得配送费3700元.第二周配送量增加,甲增加的配送量占乙、丙配送量之和的![]() ,丙增加的配送量占甲、乙、丙增加的配送量之和的
,丙增加的配送量占甲、乙、丙增加的配送量之和的![]() ,此时甲、乙的配送量之和为丙的配送量的
,此时甲、乙的配送量之和为丙的配送量的![]() 倍,丁的配送量增加60单,且他们共获得配送费7660元.若丁每单配送费高于4元且不超过8元,则第二周四位外卖员配送量之和为 单.18.在2022新春佳节即将来临之际,某商家拟推出收费定制个性新春礼品,礼品主要包含三种:对联、门神和红包,如果定制对联
倍,丁的配送量增加60单,且他们共获得配送费7660元.若丁每单配送费高于4元且不超过8元,则第二周四位外卖员配送量之和为 单.18.在2022新春佳节即将来临之际,某商家拟推出收费定制个性新春礼品,礼品主要包含三种:对联、门神和红包,如果定制对联![]() 副、门神
副、门神![]() 副、红包
副、红包![]() 个,需付人民币
个,需付人民币![]() 元;如果定制对联
元;如果定制对联![]() 副、门神
副、门神![]() 副、红包
副、红包![]() 个,需付人民币
个,需付人民币![]() 元;某人想定制
元;某人想定制![]() 副对联、
副对联、![]() 副门神、
副门神、![]() 个红包共需付人民币 元.19.某校七年级在元旦节举行了“速算大赛”,用签字笔、钢笔、圆规三种文具用品混装成甲、乙、丙三种奖品礼包,其中甲种奖品礼包包含10支签字笔、5支钢笔;乙种奖品礼包包含2支签字笔,6支钢笔,4个圆规;丙种奖品礼包包含4支签字笔,8个圆规.购买每个礼包的费用等于礼包内各文具用品的费用之和;已知两包乙奖品礼包比一包丙奖品礼包贵240元.学校采购员小李在1月1日当天,去文具店购买这三种文具用品发现,该文具店对签字笔、钢笔、圆规的售价分别打5折、7折、8折销售;1月2号恢复原价,小李发现1月1日一个乙礼包的售价比1月2日一个丙礼包售价便宜12元,若签字笔、钢笔、圆规三种文具用品的原价都是正整数,且签字笔的单价不超过10元,若小李在1月1日购买一个甲礼包和一个乙礼包,应该付 元.20.对于实数x,y定义新运算
个红包共需付人民币 元.19.某校七年级在元旦节举行了“速算大赛”,用签字笔、钢笔、圆规三种文具用品混装成甲、乙、丙三种奖品礼包,其中甲种奖品礼包包含10支签字笔、5支钢笔;乙种奖品礼包包含2支签字笔,6支钢笔,4个圆规;丙种奖品礼包包含4支签字笔,8个圆规.购买每个礼包的费用等于礼包内各文具用品的费用之和;已知两包乙奖品礼包比一包丙奖品礼包贵240元.学校采购员小李在1月1日当天,去文具店购买这三种文具用品发现,该文具店对签字笔、钢笔、圆规的售价分别打5折、7折、8折销售;1月2号恢复原价,小李发现1月1日一个乙礼包的售价比1月2日一个丙礼包售价便宜12元,若签字笔、钢笔、圆规三种文具用品的原价都是正整数,且签字笔的单价不超过10元,若小李在1月1日购买一个甲礼包和一个乙礼包,应该付 元.20.对于实数x,y定义新运算![]() 其中a,b,c为常数,若
其中a,b,c为常数,若![]() ,且有一个非零常数d,使得对于任意的x,恒有
,且有一个非零常数d,使得对于任意的x,恒有![]() ,则d的值是 . 三、解答题21.解方程组:(1)
,则d的值是 . 三、解答题21.解方程组:(1)![]() (2)
(2)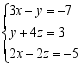 .22.对于一个三位数
.22.对于一个三位数![]() ,如果
,如果![]() 满足:它的百位数字、十位数字之和与个位数字的差等于
满足:它的百位数字、十位数字之和与个位数字的差等于![]() ,那么称这个数
,那么称这个数![]() 为“幸福数”.例如:
为“幸福数”.例如:![]() ,
,![]() ,
,![]() 是“幸福数”;
是“幸福数”;![]() ,
,![]() ,
,![]() 不是“幸福数”.(1)判断
不是“幸福数”.(1)判断![]() ,
,![]() 是否为“幸福数”?并说明理由;(2)若将一个“幸福数”
是否为“幸福数”?并说明理由;(2)若将一个“幸福数”![]() 的个位数的
的个位数的![]() 倍放到十位,原来的百位数变成个位数,原来的十位数变成百位数,得到一个新的三位数
倍放到十位,原来的百位数变成个位数,原来的十位数变成百位数,得到一个新的三位数![]() (例如:若
(例如:若![]() ,则
,则![]() ),若
),若![]() 也是一个“幸福数”,求满足条件的所有
也是一个“幸福数”,求满足条件的所有![]() 的值.23.【阅读感悟】有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是求关于未知数的代数式的值,如以下问题:已知实数x,y满足
的值.23.【阅读感悟】有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是求关于未知数的代数式的值,如以下问题:已知实数x,y满足![]() ①,
①,![]() ②,求代数式
②,求代数式![]() 和
和![]() 的值.本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的代数式得到答案.常规思路运算量比较大.其实仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值.如由
的值.本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的代数式得到答案.常规思路运算量比较大.其实仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值.如由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() .这样的解题思想就是通常所说的“整体思想”.【数学理解】(1)已知二元一次方程组
.这样的解题思想就是通常所说的“整体思想”.【数学理解】(1)已知二元一次方程组![]() 则代数式
则代数式![]() 的值为______,代数式
的值为______,代数式![]() 的值为______;【生活应用】(2)某班级组织活动购买小奖品,买20只铅笔、3块橡皮、2本日记本共需35元;买39只铅笔、5块橡皮、3本日记本共需62元.求购买9只铅笔、9块橡皮、9本日记本共需多少元?【迁移拓展】(3)对于实数x,y,定义新运算:
的值为______;【生活应用】(2)某班级组织活动购买小奖品,买20只铅笔、3块橡皮、2本日记本共需35元;买39只铅笔、5块橡皮、3本日记本共需62元.求购买9只铅笔、9块橡皮、9本日记本共需多少元?【迁移拓展】(3)对于实数x,y,定义新运算:![]() ,其中a,b,c为常数,等式右边是常规的加法和乘法运算.已知
,其中a,b,c为常数,等式右边是常规的加法和乘法运算.已知![]() ,
,![]() ,求
,求![]() 的值.24.解方程组:
的值.24.解方程组: .25.阅读下列材料,然后解答后面的问题.已知方程组
.25.阅读下列材料,然后解答后面的问题.已知方程组![]() ,求x+y+z的值.解:将原方程组整理得
,求x+y+z的值.解:将原方程组整理得![]() ,②–①,得x+3y=7③,把③代入①得,x+y+z=6.仿照上述解法,已知方程组
,②–①,得x+3y=7③,把③代入①得,x+y+z=6.仿照上述解法,已知方程组![]() ,试求x+2y–z的值.
,试求x+2y–z的值.
参考答案:1.C2.A3.C4.A5.A6.C7.B8.A9.B10.C11.11%12. ![]() ,
, ![]() .13.614.215.
.13.614.215.![]() 16.7617.123318.4119.
16.7617.123318.4119.![]() 20.421.(1)
20.421.(1)![]() ;(2)
;(2)![]() 22.(1)
22.(1)![]() 是“幸福数”,
是“幸福数”,![]() 不是“幸福数”,见解析;(2)满足条件的所有
不是“幸福数”,见解析;(2)满足条件的所有![]() 的值为:
的值为:![]() ,
,![]() 23.(1)6,2;(2)72元;(3)
23.(1)6,2;(2)72元;(3)![]() 24.
24.![]() 25.3
25.3
相关试卷
这是一份初中数学沪科版七年级上册3.5 三元一次方程组及其解法课堂检测,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份沪科版七年级上册第3章 一次方程与方程组3.5 三元一次方程组及其解法课时练习,共3页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年第3章 一次方程与方程组3.5 三元一次方程组及其解法精品课后练习题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









