


还剩19页未读,
继续阅读
所属成套资源:新版华东师大版七年级数学上册全一册教学课件
成套系列资料,整套一键下载
2023七年级数学上册第4章图形的初步认识全章综合检测教学课件新版华东师大版
展开
这是一份2023七年级数学上册第4章图形的初步认识全章综合检测教学课件新版华东师大版,共27页。
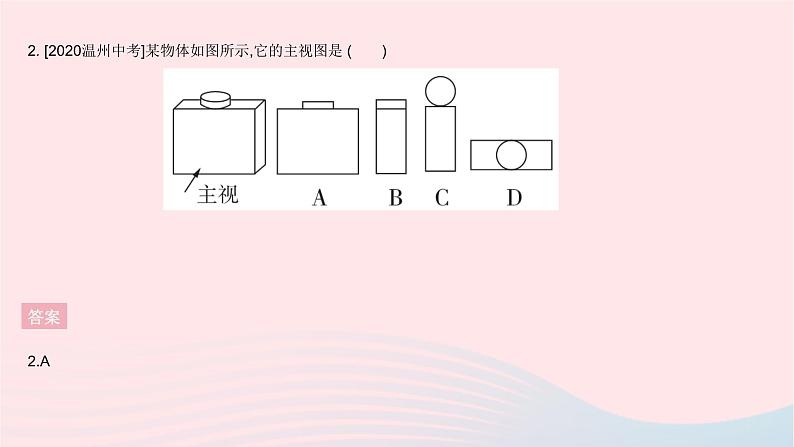
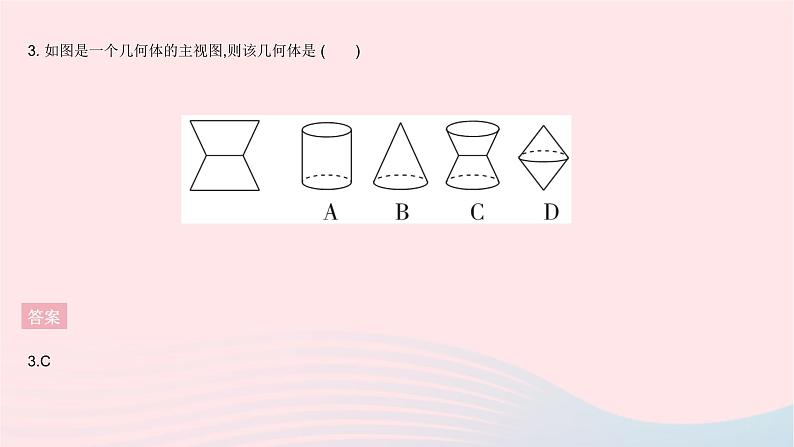
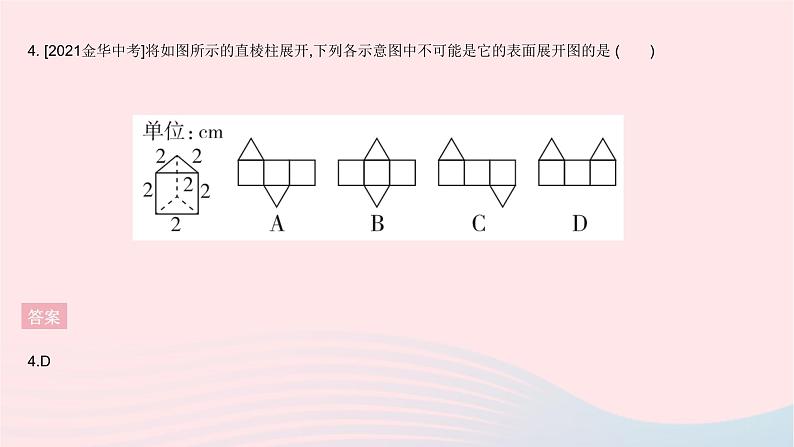
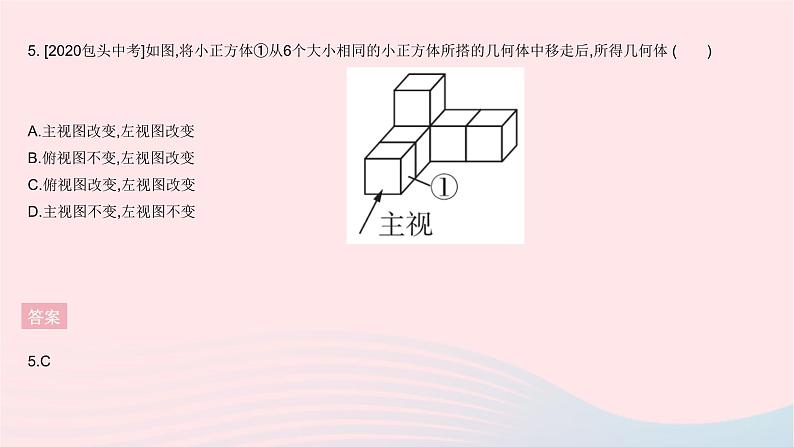
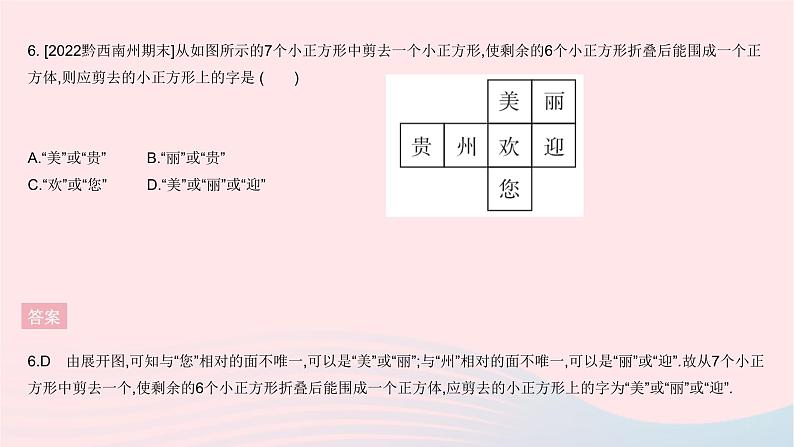
全章综合检测一、选择题1. 下列现象说明“点动成线”的是( )A.汽车雨刷在挡风玻璃上面画出的痕迹B.扔一块小石子,小石子在空中飞行的路线C.旋转一扇门,门在空中运动的痕迹D.电风扇通电后它的扇叶旋转,在空中形成的图形答案1.B2. [2020温州中考]某物体如图所示,它的主视图是 ( )答案2.A3. 如图是一个几何体的主视图,则该几何体是 ( )答案3.C4. [2021金华中考]将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是 ( )答案4.D5. [2020包头中考]如图,将小正方体①从6个大小相同的小正方体所搭的几何体中移走后,所得几何体 ( )A.主视图改变,左视图改变B.俯视图不变,左视图改变C.俯视图改变,左视图改变D.主视图不变,左视图不变答案5.C6. [2022黔西南州期末]从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去的小正方形上的字是 ( )A.“美”或“贵” B.“丽”或“贵”C.“欢”或“您” D.“美”或“丽”或“迎”答案6.D 由展开图,可知与“您”相对的面不唯一,可以是“美”或“丽”;与“州”相对的面不唯一,可以是“丽”或“迎”.故从7个小正方形中剪去一个,使剩余的6个小正方形折叠后能围成一个正方体,应剪去的小正方形上的字为“美”或“丽”或“迎”.7. 如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是 ( )A.48° B.56° C.60° D.32°答案7.B 因为OC平分∠AOB,所以∠AOB=2∠AOC=2∠BOC.因为∠COD是直角,所以∠COD=90°.因为∠BOD=118°,所以∠BOC=∠BOD-∠COD=118°-90°=28°,所以∠AOB=2∠BOC=56°.8. [2022临汾期末]如图,甲从A点出发向北偏东60°方向走至点B,乙从A点出发向南偏西25°方向走至C,则∠BAC的度数是 ( )A.85° B.115° C.135° D.145°答案8.D 由题意得,∠BAF=90°-60°=30°,所以∠BAC=∠BAF+∠EAF+∠CAE=30°+90°+25°=145°.9. [2021济南槐荫区期末]已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm.若M是AC的中点,N是BC的中点,则线段MN的长度是( )A.7 cm B.3 cm C.7 cm或3 cm D.5 cm答案 答案 二、填空题11. [2021营口中考]若∠A=34°,则∠A的补角为 °. 答案11.146 ∠A的补角=180°-∠A=180°-34°=146°.12. 新情境[2022运城盐湖区期末]“运三高铁”已被列入山西省“十四五”铁路建设规划,“运三高铁”是穿越中条山的高速铁路,大大减少了人们从运城到三门峡的时间,建造直隧道的目的可以用数学知识解释为 . 答案12.两点之间,线段最短13. 一题多解[2022石家庄新华区期中]钟表盘上的时间是11时20分,此刻时针与分针之间的夹角为 . 答案 14. 如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC=82°,则∠BOF= °. 答案 15. [2022重庆綦江区期末]正四面体的每条棱上有相同数目的小球,小球的分布特点如图所示(图中只示意了一条棱上有4个小球的情况),假设每条棱上的小球数为a,则正四面体上小球总数是 . 答案15.6a-8 因为正四面体有6条棱,所以6条棱上有6a个小球,但每个顶点处的小球被多计算了2次,4个顶点就被多计算了2×4=8(次),所以正四面体上小球总数为6a-8.三、解答题16. [2021西安碑林区期中]画出如图所示的立体图形的三视图.答案16.解:画图如下: 17. 如图所示是一个几何体的三视图(单位:cm).(1)说明组成该几何体的两部分分别是什么几何体;(2)求该几何体的体积.(结果保留π)答案17.解:(1)下面的是长方体,上面的是圆柱.(2)这个几何体的体积为30×40×26+π×(20÷2)2×26=(31 200+2 600π)(cm3).18. 如图,延长线段AB到点C,使AC=3AB,在线段AB的反向延长线上取一点D,使AD=AB.若点E是线段AB的中点,DE=7.2 cm,求线段CD的长.答案18.解:因为点E是线段AB的中点,所以AB=2AE=2BE.因为AD=AB,所以AD=2AE.因为DE=7.2 cm,所以2AE+AE=7.2 cm,所以AE=2.4 cm,所以AD=AB=2AE=4.8 cm.因为AC=3AB,所以AC=14.4 cm,所以CD=AD+AC=4.8+14.4=19.2(cm).19. 如图, O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD.(1)图中与∠DOE互余的角是 ; (2)图中与∠EOF互补的角是 ; (3)若∠EOD∶∠EOF=2∶1,求∠AOC的度数;(4)若∠AOF=60°,则OD平分∠EOC吗?请说明理由.答案19.解:(1)∠EOF,∠BOD,∠BOC(2)∠AOD,∠AOC (4)OD平分∠EOC.理由如下:因为∠BOE=90°,所以∠AOE=90°,又因为∠DOF=90°,所以∠AOF+∠EOF=90°,∠DOE+∠EOF=90°,所以∠DOE=∠AOF=60°,所以∠DOB=90°-∠DOE=90°-60°=30°.因为OB平分∠COD,所以∠DOC=2∠DOB=60°,所以∠DOC=∠DOE,所以OD平分∠EOC.20. [2022广元朝天区期末]综合与探究:将直角三角尺OAB和直角三角尺OCD按图1所示的方式放置,两个顶点重合于点O,且∠AOB=60°,∠OCD=45°,∠COD=∠ABO=90°,OE平分∠BOC,OF平分∠AOD.将三角尺OCD绕点O逆时针旋转一周的过程中(旋转中∠AOD和∠BOC均是指小于180°的角),探究∠EOF的度数.(1)当三角尺OCD绕点O旋转至图2的位置时,OB与OD重合,则∠AOC= °,∠EOF= °. (2)当三角尺OCD绕点O旋转至图3的位置时,此时B,O,D三点在同一直线上,求∠EOF的度数.(3)三角尺OCD绕点O旋转过程中,∠EOF的度数还有其他可能吗?若有,请直接写出∠EOF的度数;若没有,请说明理由.(4)类比拓展:当∠COD的度数为α(0°<α<180°)时,其他条件不变,在旋转过程中,请直接写出∠EOF的度数.(用含α的代数式表示) 答案
全章综合检测一、选择题1. 下列现象说明“点动成线”的是( )A.汽车雨刷在挡风玻璃上面画出的痕迹B.扔一块小石子,小石子在空中飞行的路线C.旋转一扇门,门在空中运动的痕迹D.电风扇通电后它的扇叶旋转,在空中形成的图形答案1.B2. [2020温州中考]某物体如图所示,它的主视图是 ( )答案2.A3. 如图是一个几何体的主视图,则该几何体是 ( )答案3.C4. [2021金华中考]将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是 ( )答案4.D5. [2020包头中考]如图,将小正方体①从6个大小相同的小正方体所搭的几何体中移走后,所得几何体 ( )A.主视图改变,左视图改变B.俯视图不变,左视图改变C.俯视图改变,左视图改变D.主视图不变,左视图不变答案5.C6. [2022黔西南州期末]从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去的小正方形上的字是 ( )A.“美”或“贵” B.“丽”或“贵”C.“欢”或“您” D.“美”或“丽”或“迎”答案6.D 由展开图,可知与“您”相对的面不唯一,可以是“美”或“丽”;与“州”相对的面不唯一,可以是“丽”或“迎”.故从7个小正方形中剪去一个,使剩余的6个小正方形折叠后能围成一个正方体,应剪去的小正方形上的字为“美”或“丽”或“迎”.7. 如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是 ( )A.48° B.56° C.60° D.32°答案7.B 因为OC平分∠AOB,所以∠AOB=2∠AOC=2∠BOC.因为∠COD是直角,所以∠COD=90°.因为∠BOD=118°,所以∠BOC=∠BOD-∠COD=118°-90°=28°,所以∠AOB=2∠BOC=56°.8. [2022临汾期末]如图,甲从A点出发向北偏东60°方向走至点B,乙从A点出发向南偏西25°方向走至C,则∠BAC的度数是 ( )A.85° B.115° C.135° D.145°答案8.D 由题意得,∠BAF=90°-60°=30°,所以∠BAC=∠BAF+∠EAF+∠CAE=30°+90°+25°=145°.9. [2021济南槐荫区期末]已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm.若M是AC的中点,N是BC的中点,则线段MN的长度是( )A.7 cm B.3 cm C.7 cm或3 cm D.5 cm答案 答案 二、填空题11. [2021营口中考]若∠A=34°,则∠A的补角为 °. 答案11.146 ∠A的补角=180°-∠A=180°-34°=146°.12. 新情境[2022运城盐湖区期末]“运三高铁”已被列入山西省“十四五”铁路建设规划,“运三高铁”是穿越中条山的高速铁路,大大减少了人们从运城到三门峡的时间,建造直隧道的目的可以用数学知识解释为 . 答案12.两点之间,线段最短13. 一题多解[2022石家庄新华区期中]钟表盘上的时间是11时20分,此刻时针与分针之间的夹角为 . 答案 14. 如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC=82°,则∠BOF= °. 答案 15. [2022重庆綦江区期末]正四面体的每条棱上有相同数目的小球,小球的分布特点如图所示(图中只示意了一条棱上有4个小球的情况),假设每条棱上的小球数为a,则正四面体上小球总数是 . 答案15.6a-8 因为正四面体有6条棱,所以6条棱上有6a个小球,但每个顶点处的小球被多计算了2次,4个顶点就被多计算了2×4=8(次),所以正四面体上小球总数为6a-8.三、解答题16. [2021西安碑林区期中]画出如图所示的立体图形的三视图.答案16.解:画图如下: 17. 如图所示是一个几何体的三视图(单位:cm).(1)说明组成该几何体的两部分分别是什么几何体;(2)求该几何体的体积.(结果保留π)答案17.解:(1)下面的是长方体,上面的是圆柱.(2)这个几何体的体积为30×40×26+π×(20÷2)2×26=(31 200+2 600π)(cm3).18. 如图,延长线段AB到点C,使AC=3AB,在线段AB的反向延长线上取一点D,使AD=AB.若点E是线段AB的中点,DE=7.2 cm,求线段CD的长.答案18.解:因为点E是线段AB的中点,所以AB=2AE=2BE.因为AD=AB,所以AD=2AE.因为DE=7.2 cm,所以2AE+AE=7.2 cm,所以AE=2.4 cm,所以AD=AB=2AE=4.8 cm.因为AC=3AB,所以AC=14.4 cm,所以CD=AD+AC=4.8+14.4=19.2(cm).19. 如图, O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD.(1)图中与∠DOE互余的角是 ; (2)图中与∠EOF互补的角是 ; (3)若∠EOD∶∠EOF=2∶1,求∠AOC的度数;(4)若∠AOF=60°,则OD平分∠EOC吗?请说明理由.答案19.解:(1)∠EOF,∠BOD,∠BOC(2)∠AOD,∠AOC (4)OD平分∠EOC.理由如下:因为∠BOE=90°,所以∠AOE=90°,又因为∠DOF=90°,所以∠AOF+∠EOF=90°,∠DOE+∠EOF=90°,所以∠DOE=∠AOF=60°,所以∠DOB=90°-∠DOE=90°-60°=30°.因为OB平分∠COD,所以∠DOC=2∠DOB=60°,所以∠DOC=∠DOE,所以OD平分∠EOC.20. [2022广元朝天区期末]综合与探究:将直角三角尺OAB和直角三角尺OCD按图1所示的方式放置,两个顶点重合于点O,且∠AOB=60°,∠OCD=45°,∠COD=∠ABO=90°,OE平分∠BOC,OF平分∠AOD.将三角尺OCD绕点O逆时针旋转一周的过程中(旋转中∠AOD和∠BOC均是指小于180°的角),探究∠EOF的度数.(1)当三角尺OCD绕点O旋转至图2的位置时,OB与OD重合,则∠AOC= °,∠EOF= °. (2)当三角尺OCD绕点O旋转至图3的位置时,此时B,O,D三点在同一直线上,求∠EOF的度数.(3)三角尺OCD绕点O旋转过程中,∠EOF的度数还有其他可能吗?若有,请直接写出∠EOF的度数;若没有,请说明理由.(4)类比拓展:当∠COD的度数为α(0°<α<180°)时,其他条件不变,在旋转过程中,请直接写出∠EOF的度数.(用含α的代数式表示) 答案
相关资料
更多









