

2022-2023学年湖南省怀化市新晃县七年级(下)期末数学试卷(含解析)
展开2022-2023学年湖南省怀化市新晃县七年级(下)期末数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
A.  B.
B.  C.
C.  D.
D. 
A. 过![]() 可画直线垂直于
可画直线垂直于![]() B. 过
B. 过![]() 可画直线
可画直线![]() 的垂线
的垂线
C. 连结![]() 使
使![]() D. 过
D. 过![]() 可画直线与
可画直线与![]() 垂直
垂直
3. 下列计算正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
9. 计算![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共6小题,共24.0分)
12. 已知一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,将这组数据中的每个数据都减去
,将这组数据中的每个数据都减去![]() ,得到一组新数据,则这组新数据的方差是______ .
,得到一组新数据,则这组新数据的方差是______ .
15. 若![]() ,
,![]() ,则
,则![]() ______ .
______ .
16. 甲、乙两个同学分解因式![]() 时,甲看错了
时,甲看错了![]() ,分解结果为
,分解结果为![]() ;乙看错了
;乙看错了![]() ,分解结果为
,分解结果为![]() ,则正确的分解结果为______ .
,则正确的分解结果为______ .
三、解答题(本大题共8小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. ![]() 本小题
本小题![]() 分
分![]()
解方程组:![]() ;
;![]() .
.
18. ![]() 本小题
本小题![]() 分
分![]()
因式分解:![]() .
.
19. ![]() 本小题
本小题![]() 分
分![]()
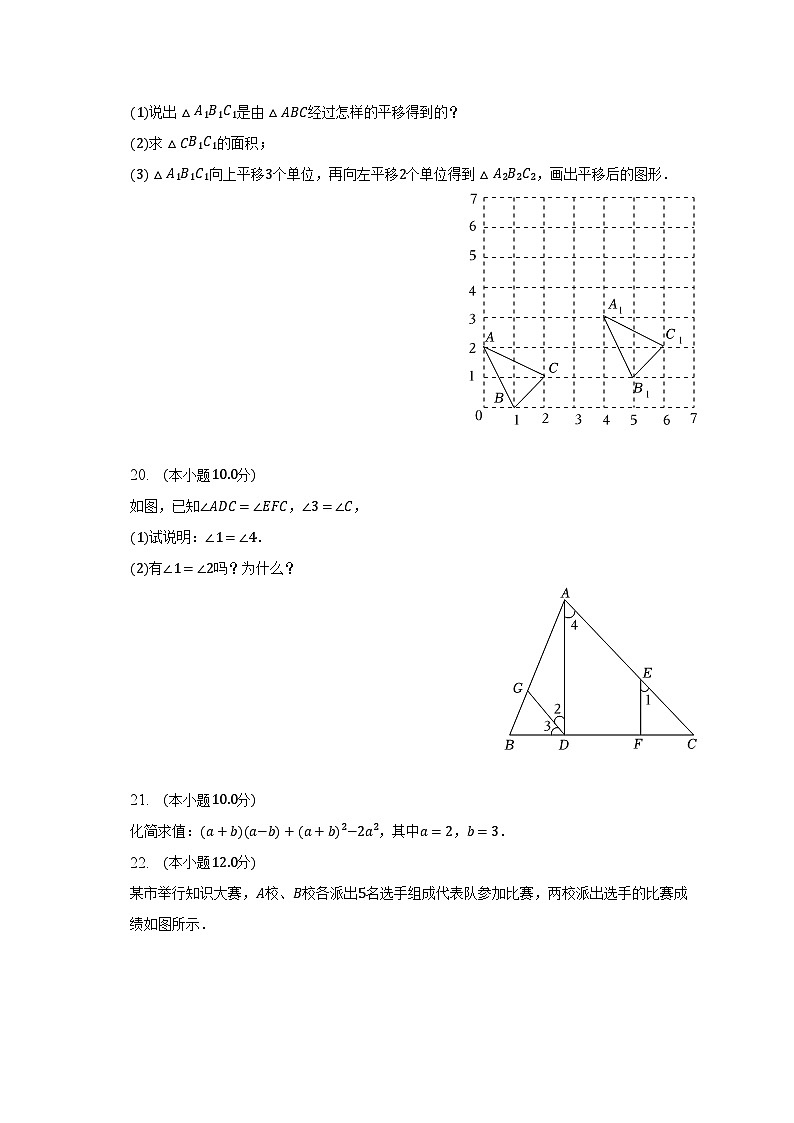
已知如图.![]() 说出
说出![]() 是由
是由![]() 经过怎样的平移得到的?
经过怎样的平移得到的?![]() 求
求![]() 的面积;
的面积;![]() 向上平移
向上平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位得到
个单位得到![]() ,画出平移后的图形.
,画出平移后的图形.
|
|
21. ![]() 本小题
本小题![]() 分
分![]()
化简求值:![]() ,其中
,其中![]() ,
,![]() .
.
22. ![]() 本小题
本小题![]() 分
分![]()
某市举行知识大赛,![]() 校、
校、![]() 校各派出
校各派出![]() 名选手组成代表队参加比赛,两校派出选手的比赛成绩如图所示.
名选手组成代表队参加比赛,两校派出选手的比赛成绩如图所示.
根据以上信息、整理分析数据:
| 平均数 | 中位数 | 众数 |
|
|
|
|
|
|
|
|
![]() ______ ,
______ ,![]() ______ .
______ .![]() 填空:
填空:![]() 填“
填“![]() 校”或“
校”或“![]() 校”
校”![]()
![]() 从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是______ ;
从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是______ ;![]() 从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是______ ;
从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是______ ;![]() 校比赛成绩的方差为______ ,
校比赛成绩的方差为______ ,![]() 校比赛成绩的方差为______ ,从两校比赛成绩的平均数和方差的角度来比较,______ 代表队选手成绩更稳定.
校比赛成绩的方差为______ ,从两校比赛成绩的平均数和方差的角度来比较,______ 代表队选手成绩更稳定.
23. ![]() 本小题
本小题![]() 分
分![]()
用![]() 辆
辆![]() 型车和
型车和![]() 辆
辆![]() 型车载满货物一次可运货
型车载满货物一次可运货![]() 吨;用
吨;用![]() 辆
辆![]() 型车和
型车和![]() 辆
辆![]() 型车载满货物一次可运货
型车载满货物一次可运货![]() 吨.某物流公司现有
吨.某物流公司现有![]() 吨货物,计划同时租用
吨货物,计划同时租用![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆,一次运完,且恰好每辆车都载满货物,根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都载满货物,根据以上信息,解答下列问题:
![]() 辆
辆![]() 型车和
型车和![]() 辆车
辆车![]() 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?
![]() 请你帮该物流公司设计租车方案;
请你帮该物流公司设计租车方案;
![]() 若
若![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次,
次,![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次.请选出最省钱的租车方案,并求出最少租车费.
次.请选出最省钱的租车方案,并求出最少租车费.
答案和解析
1.【答案】![]()
【解析】解:![]() 是轴对称图形,故本选项符合题意;
是轴对称图形,故本选项符合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项不合题意.
故选:![]() .
.
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】![]()
【解析】解:![]() 、
、![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 为
为![]() 外一点,
外一点,![]() 可以过
可以过![]() 可画直线垂直于
可画直线垂直于![]() ,正确,不合题意;
,正确,不合题意;
B、![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 为
为![]() 外一点,
外一点,![]() 过
过![]() 可画直线
可画直线![]() 的垂线,正确,不合题意;
的垂线,正确,不合题意;
C、连接![]() 不能保证
不能保证![]() ,故错误,符合题意;
,故错误,符合题意;
D、![]() 为
为![]() 外一点,
外一点,![]() 可以过
可以过![]() 可画直线与
可画直线与![]() 垂直,正确,不合题意;
垂直,正确,不合题意;
故选:![]() .
.
直接利用垂线的定义结合垂线作法得出答案.
此题主要考查了垂线的作法以及垂线的定义,正确把握垂线的作法是解题关键.
3.【答案】![]()
【解析】解:![]() 、
、![]() ,故A不符合题意;
,故A不符合题意;
B、![]() ,故B不符合题意;
,故B不符合题意;
C、![]() ,故C不符合题意;
,故C不符合题意;
D、![]() ,故D符合题意;
,故D符合题意;
故选:![]() .
.
利用完全平方公式,多项式乘多项式的法则,平方差公式对各项进行运算即可.
本题主要考查整式的混合运算,解答的关键是对相应的运算法则的掌握.
4.【答案】![]()
【解析】解:![]() 无法利用平方差公式计算,则
无法利用平方差公式计算,则![]() 不符合题意;
不符合题意;![]() 无法利用平方差公式计算,则
无法利用平方差公式计算,则![]() 不符合题意;
不符合题意;![]() ,它可以利用平方差公式计算,则
,它可以利用平方差公式计算,则![]() 符合题意;
符合题意;![]() ,它可以利用完全平方公式计算,则
,它可以利用完全平方公式计算,则![]() 不符合题意;
不符合题意;
故选:![]() .
.
根据平方差公式及完全平方公式的形式进行判断即可.
本题考查完全平方式和平方差公式,熟练掌握两个公式是解题的关键.
5.【答案】![]()
【解析】解:将![]() 代入原方程得:
代入原方程得:![]() ,
,
解得:![]() ,
,![]() 的值为
的值为![]() .
.
故选:![]() .
.
将![]() 代入原方程,可得出关于
代入原方程,可得出关于![]() 的一元一次方程,解之即可求出
的一元一次方程,解之即可求出![]() 的值.
的值.
本题考查了二元一次方程的解,牢记“把方程的解代入原方程,等式左右两边相等”是解题的关键.
6.【答案】![]()
【解析】解:![]() ,
,![]() .
.
故选:![]() .
.
由两直线平行,同位角相等,即可得到答案.
本题考查平行线的性质,关键是掌握两直线平行,同位角相等.
7.【答案】![]()
【解析】解:![]() ,
,![]() ,
,![]()
![]()
![]() .
.
故选:![]() .
.
根据垂线的定义可知![]() ,由
,由![]() ,从而可求出答案.
,从而可求出答案.
本题考查垂线定义,解题的关键正确运用垂线的定义求出相关的角的度数,本题属于基础题型.
8.【答案】![]()
【解析】解:![]()
![]()
![]() ,
,![]() 结果中不含
结果中不含![]() 的一次项,
的一次项,![]() ,
,
解得:![]() .
.
故选:![]() .
.
利用多项式乘多项式的法则进行运算,再结合结果不含![]() 的一次项,则其系数为
的一次项,则其系数为![]() ,从而可求解.
,从而可求解.
本题主要考查多项式乘多项式,解答的关键是明确不含![]() 的一次项,则其系数为
的一次项,则其系数为![]() .
.
9.【答案】![]()
【解析】解:![]()
![]()
![]()
![]()
![]()
![]() .
.
故选:![]() .
.
利用积的乘方的法则进行运算即可.
本题主要考查积的乘方,解答的关键是对相应的运算法则的掌握.
10.【答案】![]()
【解析】解:由题意得:![]() ,
,![]() 得:
得:![]() ,
,
把![]() 代入
代入![]() 中得:
中得:![]() ,
,
解得:![]() ,
,![]() 原方程组的解为:
原方程组的解为:![]() ,
,
把![]() 代入方程组
代入方程组![]() 中可得:
中可得:![]() ,
,
解得:![]() ,
,![]() ,
,
故选:![]() .
.
先联立不含![]() ,
,![]() 的两个方程,解方程组求出
的两个方程,解方程组求出![]() ,
,![]() 的值,再代入含
的值,再代入含![]() ,
,![]() 的两个方程联立的方程组中,进行计算即可解答.
的两个方程联立的方程组中,进行计算即可解答.
本题考查了二元一次方程组的解,熟练掌握同解方程组是解题的关键.
11.【答案】![]()
【解析】解:![]() ,
,
故答案为:![]() .
.
本题主要根据提公因式法把多项式分解因式,从而找出公因式.
本题主要考查了因式分解的相关知识,难度不大,找出公因式是关键.
12.【答案】![]()
【解析】解:已知一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,将这组数据中的每个数据都减去
,将这组数据中的每个数据都减去![]() ,得到一组新数据,则这组新数据的方差是
,得到一组新数据,则这组新数据的方差是![]() .
.
故答案为:![]() .
.
方差是用来衡量一组数据波动大小的量,每个数都减去![]() 所以波动不会变,方差不变.
所以波动不会变,方差不变.
本题考查方差、算术平均数,解答本题的关键是明确题意,会计算一组数据的方差和平均数.
13.【答案】![]()
【解析】解:![]() 直线
直线![]() ,直线
,直线![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故答案为:![]() .
.
首先证明![]() ,可得
,可得![]() ,再根据
,再根据![]() 即可解决问题.
即可解决问题.
本题考查平行线的判定和性质、邻补角的性质等知识,灵活运用知识是解决问题的关键.
14.【答案】![]()
【解析】解:![]() 多项式
多项式![]() 是完全平方式,且
是完全平方式,且![]() ,
,![]() .
.
故答案为:![]() .
.
根据多项式![]() 是完全平方式,且
是完全平方式,且![]() ,可得:
,可得:![]() ,据此求出
,据此求出![]() 的值是多少即可.
的值是多少即可.
此题主要考查了完全平方公式的应用,要熟练掌握,解答此题的关键是要明确:![]() .
.
15.【答案】![]()
【解析】解:![]() ,
,![]() ,
,![]() ,
,![]() .
.
故答案为:![]() .
.
直接利用同底数幂的乘法运算法则将已知变形,进而得出答案.
此题主要考查了同底数幂的乘法,正确将已知变形是解题关键.
16.【答案】![]()
【解析】解:![]() 甲看错了
甲看错了![]() ,分解结果为
,分解结果为![]() ,
,![]() 由
由![]() ,可知
,可知 ![]() ,
,
又![]() 乙看错了
乙看错了![]() ,分解结果为
,分解结果为![]() ,
,![]() 由
由![]() ,可知
,可知![]() ,
,![]() ,
,![]() ,
,![]() 正确的分解结果为
正确的分解结果为![]() .
.
故答案为:![]() .
.
根据题意分别运算![]() 和
和![]() ,确定
,确定![]() 、
、![]() 的值,然后进行因式分解即可.
的值,然后进行因式分解即可.
本题主要考查了因式分解的知识,整式乘法运算,解决本题的关键是理解题意,求出![]() 、
、![]() 的值.
的值.
17.【答案】解:![]() 得,
得,![]() ,
,
解得![]() ;
;
把![]() 代入
代入![]() 得,
得,![]() ,
,
解得![]() ,
,
故方程组的解为![]() ;
;![]() 得,
得,![]() ,
,
解得![]() ;
;
把![]() 代入
代入![]() 得,
得,![]() ,
,
解得![]() ,
,
故方程组的解为![]() .
.
【解析】![]() 先用加减消元法求出
先用加减消元法求出![]() 的值,再用代入消元法求出
的值,再用代入消元法求出![]() 的值即可;
的值即可;![]() 先用加减消元法求出
先用加减消元法求出![]() 的值,再用代入消元法求出
的值,再用代入消元法求出![]() 的值即可.
的值即可.
本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解题的关键.
18.【答案】解:原式![]()
![]() .
.
【解析】原式提取公因式,再利用平方差公式分解即可.
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
19.【答案】解:![]() 经过向上平移
经过向上平移![]() 个单位,向右平移
个单位,向右平移![]() 个单位得到
个单位得到![]() ;
;![]() 的面积
的面积![]() ;
;![]() 如图,
如图,![]() 即为所求作.
即为所求作.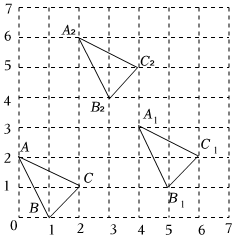
【解析】![]() 利用平移的性质解决问题即可;
利用平移的性质解决问题即可;![]() 利用三角形面积公式即可求解;
利用三角形面积公式即可求解;![]() 利用平移的性质分别作出
利用平移的性质分别作出![]() 、
、![]() 、
、![]() 的对应点
的对应点![]() 、
、![]() 、
、![]() 即可.
即可.
本题考查作图![]() 平移变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
平移变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
20.【答案】![]() 证明:
证明:![]() ,
,![]() 同位角相等,两直线平行
同位角相等,两直线平行![]() ,
,![]() 两直线平行,同位角相等
两直线平行,同位角相等![]() .
.![]() 解:有
解:有![]() ,理由如下:
,理由如下:![]() ,
,![]() ,
,![]() 是
是![]() 的一个外角,
的一个外角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】![]() 根据同位角相等,两直线平行得出
根据同位角相等,两直线平行得出![]() ,再由平行得出角相等即可;
,再由平行得出角相等即可;![]() 根据三角形的外角等于不相邻的外角之和,可知
根据三角形的外角等于不相邻的外角之和,可知![]() ,由
,由![]() 即可得出
即可得出![]() .
.
本题考查了平行线的判定与性质,熟记平行线的判定方法和性质是解题关键.
21.【答案】解:![]() ,
,![]()
![]() ,
,
当![]() ,
,![]() 时,原式
时,原式![]() .
.
【解析】先根据完全平方公式和平方差公式进行计算,再合并同类项,最后代入求出答案即可.
本题考查了整式的化简求值,能正确根据整式的运算法则进行计算是解此题的关键,注意运算顺序.
22.【答案】![]()
![]()
![]() 校
校 ![]() 校
校 ![]()
![]()
![]() 校
校
【解析】解:![]() 条形统计图可知:
条形统计图可知:![]() 校
校![]() 名选手的成绩从小到大排列后分别为:
名选手的成绩从小到大排列后分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
![]() 校
校![]() 名选手的成绩的中位数为
名选手的成绩的中位数为![]() ,众数为
,众数为![]() ,
,![]() ,
,![]()
故答案为:![]() ,
,![]() ;
;![]() 两校的平均数相同,
两校的平均数相同,![]() 校的中位数
校的中位数![]() 校的中位数,
校的中位数,![]() 从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是
从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是![]() 校,
校,
故答案为:![]() 校;
校;![]() 两校的平均数相同,
两校的平均数相同,![]() 校的众数
校的众数![]() 校的众数,
校的众数,![]() 从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是
从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是![]() 校,
校,
故答案为:![]() 校;
校;![]() 校的方差
校的方差![]() ,
,![]() 校的方差
校的方差![]() ,
,![]() ,
,![]() 从两校比赛成绩的方差的角度来比较,
从两校比赛成绩的方差的角度来比较,![]() 校代表队选手成绩的方差较大,
校代表队选手成绩的方差较大,
故A校代表队选手成绩更稳定.![]() 根据中位数的定义和众数的定义即可求出
根据中位数的定义和众数的定义即可求出![]() 和
和![]() 的值;
的值;![]() 根据平均数和中位数的意义即可得出结论;
根据平均数和中位数的意义即可得出结论;![]() 根据平均数和众数的意义即可得出结论;
根据平均数和众数的意义即可得出结论;![]() 求出两个代表队的方差即可得出结论.
求出两个代表队的方差即可得出结论.
本题考查的是条形统计图和统计表及用各统计量作决策,掌握各统计量的定义、公式及意义是解题关键.
23.【答案】解:![]() 设每辆
设每辆![]() 型车、
型车、![]() 型车都装满货物一次可以分别运货
型车都装满货物一次可以分别运货![]() 吨、
吨、![]() 吨,
吨,
依题意列方程组得:![]() ,
,
解方程组,得:![]() ,
,
答:![]() 辆
辆![]() 型车装满货物一次可运
型车装满货物一次可运![]() 吨,
吨,![]() 辆
辆![]() 型车装满货物一次可运
型车装满货物一次可运![]() 吨.
吨.![]() 结合题意和
结合题意和![]() 得:
得:![]() ,
,![]()
![]() 、
、![]() 都是正整数
都是正整数![]() 或
或![]() 或
或![]()
答:有![]() 种租车方案:
种租车方案:
方案一:![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆;
辆;
方案二:![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆;
辆;
方案三:![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆.
辆.![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次,
次,![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次,
次,![]() 方案一需租金:
方案一需租金:![]() 元
元![]()
方案二需租金:![]() 元
元![]()
方案三需租金:![]() 元
元![]()
![]()
![]() 最省钱的租车方案是方案三:
最省钱的租车方案是方案三:![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆,最少租车费为
辆,最少租车费为![]() 元.
元.
【解析】本题主要考查了二元一次方程组和二元一次方程的实际应用,此题型是各地中考的热点,同学们在平时练习时要加强训练,属于中档题.![]() 根据“用
根据“用![]() 辆
辆![]() 型车和
型车和![]() 辆
辆![]() 型车载满货物一次可运货
型车载满货物一次可运货![]() 吨;”“用
吨;”“用![]() 辆
辆![]() 型车和
型车和![]() 辆
辆![]() 型车载满货物一次可运货
型车载满货物一次可运货![]() 吨”,分别得出等式方程,组成方程组求出即可;
吨”,分别得出等式方程,组成方程组求出即可;![]() 由题意理解出:
由题意理解出:![]() ,解此二元一次方程,求出其整数解,得到三种租车方案;
,解此二元一次方程,求出其整数解,得到三种租车方案;![]() 根据
根据![]() 中所求方案,利用
中所求方案,利用![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次,
次,![]() 型车每辆需租金
型车每辆需租金![]() 元
元![]() 次,分别求出租车费用即可.
次,分别求出租车费用即可.
24.【答案】![]()
【解析】解:![]() 正方形面积为
正方形面积为![]() ,小块四边形面积总和为
,小块四边形面积总和为![]()
![]() 由面积相等可得:
由面积相等可得:![]() ,
,
故答案为:![]() .
.![]() 由
由![]() 可知
可知![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() .
.![]() 由题意知,
由题意知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,
又![]() 为定值,
为定值,![]() ,即
,即![]() .
.![]() 正方形面积为
正方形面积为![]() ,小块四边形面积总和为
,小块四边形面积总和为![]() ,由面积相等即可求解;
,由面积相等即可求解;![]() 根据
根据![]() 中的结论,将式子的值代入计算即可求解;
中的结论,将式子的值代入计算即可求解;![]() ,
,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,即可求解.
,即可求解.
本题主要考查多项式乘多项式,掌握整式混合运算法则是解题的关键.
2022-2023学年湖南省怀化市新晃县八年级(上)期末数学试卷(含解析): 这是一份2022-2023学年湖南省怀化市新晃县八年级(上)期末数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖南省怀化市新晃县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年湖南省怀化市新晃县七年级(下)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖南省怀化市新晃县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年湖南省怀化市新晃县八年级(下)期末数学试卷(含解析),共21页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。


















