2022-2023学年湖北省恩施州恩施市沙地、崔坝、双河、新塘四校八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年湖北省恩施州恩施市沙地、崔坝、双河、新塘四校八年级（下）期中数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年湖北省恩施州恩施市沙地、崔坝、双河、新塘四校八年级（下）期中数学试卷
一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列二次根式中是最简二次根式的是(    )
A. 12 B. x2+1 C. 15 D. a2
2. 下列各组数中，是勾股数的一组是(    )
A. 13，14，15 B. 40，9，41 C. 3，4， 5 D. 1，34，54
3. 下列计算正确的是(    )
A. (−a)2=−a B. ( a)2=a C. a2=a D. ( −a)2=a
4. 如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为(    )
A. 2 55
B. 3 55
C. 4 55
D. 45
5. 计算( 2−1)2022⋅( 2+1)2023的结果为(    )
A. 2+1 B. 2−1 C. 1− 2 D. 1
6. 若 2x−1x−3在实数范围内有意义，则x的取值范围是(    )
A. x≠3 B. x>12且x≠3 C. x≥2 D. x≥12且x≠3
7. 已知实数a、b在数轴上的位置如图所示，则化简代数式 a2− b2− (a−b)2的结果是(    )


A. −2b B. −2a C. 0 D. 2b−2a
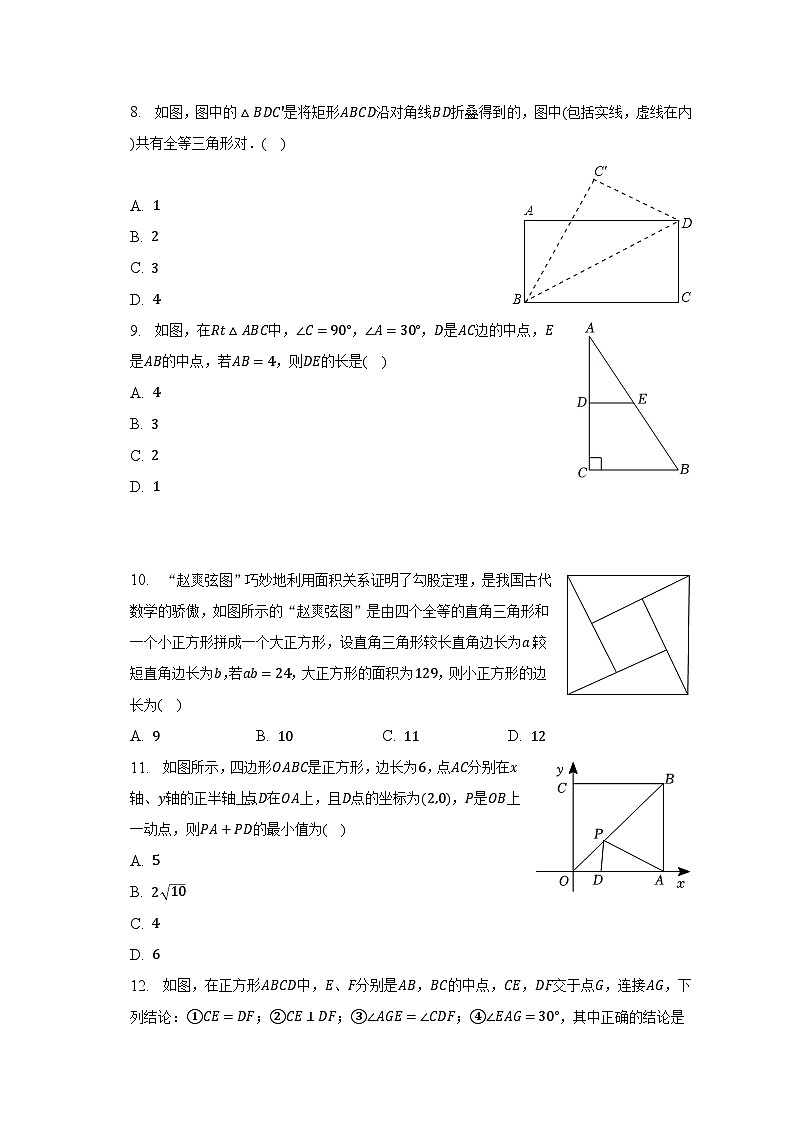
8. 如图，图中的△BDC′是将矩形ABCD沿对角线BD折叠得到的，图中(包括实线，虚线在内)共有全等三角形对．(    )

A. 1
B. 2
C. 3
D. 4
9. 如图，在Rt△ABC中，∠C=90°，∠A=30°，D是AC边的中点，E是AB的中点，若AB=4，则DE的长是(    )
A. 4
B. 3
C. 2
D. 1


10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若ab=24，大正方形的面积为129，则小正方形的边长为(    )
A. 9 B. 10 C. 11 D. 12
11. 如图所示，四边形OABC是正方形，边长为6，点AC分别在x轴、y轴的正半轴上，点D在OA上，且D点的坐标为(2,0)，P是OB上一动点，则PA+PD的最小值为(    )
A. 5
B. 2 10
C. 4
D. 6
12. 如图，在正方形ABCD中，E、F分别是AB，BC的中点，CE，DF交于点G，连接AG，下列结论：①CE=DF；②CE⊥DF；③∠AGE=∠CDF；④∠EAG=30°，其中正确的结论是(    )


A. ①② B. ①③ C. ①②④ D. ①②③
二、填空题（本大题共4小题，共12.0分）
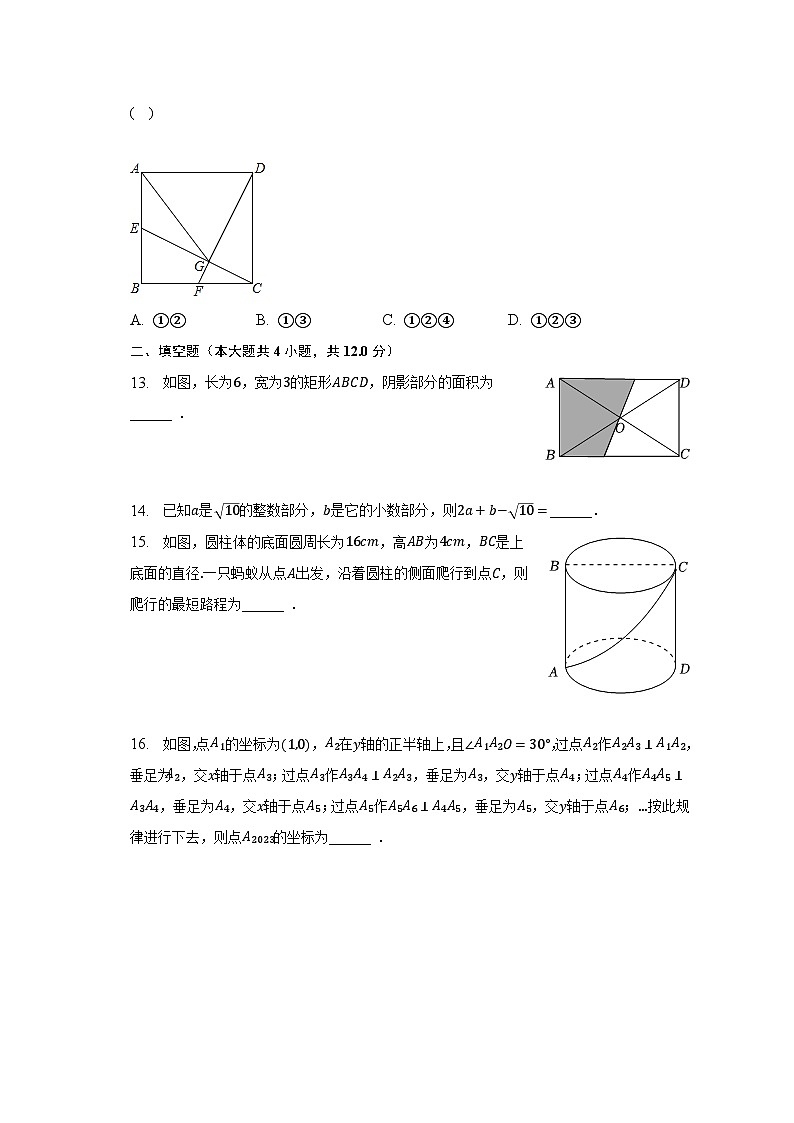
13. 如图，长为6，宽为3的矩形ABCD，阴影部分的面积为______ ．


14. 已知a是 10的整数部分，b是它的小数部分，则2a+b− 10=______．
15. 如图，圆柱体的底面圆周长为16cm，高AB为4cm，BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，则爬行的最短路程为______ ．


16. 如图，点A1的坐标为(1,0)，A2在y轴的正半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交x轴于点A3；过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交x轴于点A5；过点A5作A5A6⊥A4A5，垂足为A5，交y轴于点A6；…按此规律进行下去，则点A2023的坐标为______ ．

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题8.0分)
计算题：
(1)(−13)−1−(3.14−π)0+| 2−2|−22+ 2；
(2)(2 12−4 18+3 48)×5 2．
18. (本小题8.0分)
先化简，再求值：2aa+1−2a−4a2−1÷a−2a2−2a+1，其中a= 2−1．
19. (本小题8.0分)
如图，小明爸爸在鱼池边开了一块四边形土地种了一些蔬菜，爸爸让小明计算这块土地的面积，以便估算产量．小明测得AB=3m，AD=4m，CD=12m，BC=13m，又已知∠A=90°.求这块土地的面积．

20. (本小题8.0分)
已知：如图，四边形ABCD是平行四边形，P，Q是对角线BD上的两个点，且BP=DQ.求证：AP//QC，AP=QC．

21. (本小题8.0分)
如图，在菱形ABCD中，BE⊥AD于点E，BF⊥CD于点F．
(1)求证：BE=BF．
(2)当DE=4，CF=2时，求菱形ABCD的面积．

22. (本小题10.0分)
在一次海上救援中，两艘专业救助船A、B同时收到某事故渔船P的求救讯息，已知此时救助船B在A的正北方向，事故渔船P在救助船A的北偏西30°方向上，在救助船B的西南方向上，且事故渔船P与救助船A相距60海里．
(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号)；
(2)求救助船A、B分别以20海里/小时，15海里/小时的速度同时出发，匀速直线前往事故渔船P处搜救，试通过计算判断哪艘船先到达．

23. (本小题10.0分)
在四边形ABCD中，AD//BC，BC⊥CD，AD=6cm，BC=10cm，点E从点A出发以1cm/s的速度向点D运动，点F从点B出发，以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t，
(1)t取何值时，四边形EFCD为矩形？
(2)M是BC上一点，且BM=4，t取何值时，以A、M、E、F为顶点的四边形是平行四边形？

24. (本小题12.0分)
平面直角坐标系中有正方形AOBC，O为坐标原点，点A、B分别在y轴、x轴正半轴上，点P、E、F分别为边BC、AC、OB上的点，EF⊥OP于M．

(1)如图1，若点E与点A重合，点A坐标为(0,8)，OF=3，求P点坐标；
(2)如图2，若点E与点A重合，且P为边BC的中点，求证：CM=2CP；
(3)如图3，若点M为线段OP的中点，连接AB交EF于点N，连接NP，试探究线段OP与NP的数量关系，并证明你的结论．
答案和解析

1.【答案】B 
【解析】
【分析】
本题主要考查了最简二次根式的定义．根据最简二次根式的定义，即可进行解答．
【解答】
解：A、 12=2 3不是最简二次根式，故A不符合题意；
B、 x2+1是最简二次根式，故B符合题意；
C、 15= 55不是最简二次根式，故C不符合题意；
D、 a2=|a|不是最简二次根式，故D不符合题意，
故选：B．  
2.【答案】B 
【解析】解：A、132+142≠152，故不是勾股数，故选项不符合题意；
B、92+402=412，能构成直角三角形，都是整数，是勾股数，故选项符合题意；
C、3，4， 5，不都是正整数，不是勾股数，故选项不符合题意；
D、1，34，54，不都是正整数，不是勾股数，故选项不符合题意．
故选：B．
欲判断是否为勾股数，必须根据勾股数是正整数，同时还需验证两小边的平方和是否等于最长边的平方．
此题主要考查了勾股数，关键是掌握勾股数的定义，及勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．

3.【答案】B 
【解析】解：A选项 (−a)2=|a|，当a>0， (−a)2=|a|=a，故错误，不符合题意；
B选项( a)2=a，所以正确，符合题意；
C选项 a2=|a|，当a