2022-2023学年湖南省永州市零陵区八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年湖南省永州市零陵区八年级（下）期末数学试卷（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年湖南省永州市零陵区八年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列文字中是中心对称图形的是(    )
A. 端 B. 午 C. 节 D. 日
2. 如图是某校门口的电动伸缩门，电动伸缩门利用了性质(    )

A. 四边形的不稳定性 B. 三角形的稳定性 C. 四边形的稳定性 D. 三角形的不稳定性
3. 若正比例函数y=kx(k≠0)的函数值y随x的增大而减少，则一次函数y=2x−k的图象大致是(    )
A. B.
C. D.
4. 如图，在Rt△ABC中，∠ABC=90°，点D是AC边上的中点，∠ADB=120°，则∠C=(    )
A. 30°
B. 60°
C. 25°
D. 45°
5. 如图，小明与小亮在玩“五子棋”，小明是黑子，他把第四子下在棋盘坐标的(1,−2)上，则小亮下的白色第三子的棋盘坐标是(    )

A. (2,6) B. (6,−2) C. (−6,−2) D. (6,2)
6. 勾股定理现约有500多种证明方法，是数学定理中证明方法最多的定理之一，在中国周朝的商定提出了“勾三股四弦五”的勾股定理的特例，古埃及人用“结绳法”在金字塔等建筑的拐角处作出直角；“普林顿322”的古巴比伦泥板上记载了很多勾股数；公元前6世纪古希腊的毕达哥拉斯学派用演绎法证明了勾股定理.下面图例中，不能证明勾股定理的是(    )
A. B. C. D.
7. 下列关系中，属于成正比例函数关系的是(    )
A. 正方形的面积与边长 B. 三角形的周长与边长
C. 圆的面积与它的半径 D. 速度一定时，路程与时间
8. 如图，正方形ABCD的边长为4，建立平面直角坐标系后，表示点D的坐标正确的是(    )

A. (4,0) B. (2,−2) C. (0,4) D. (−2,−4)
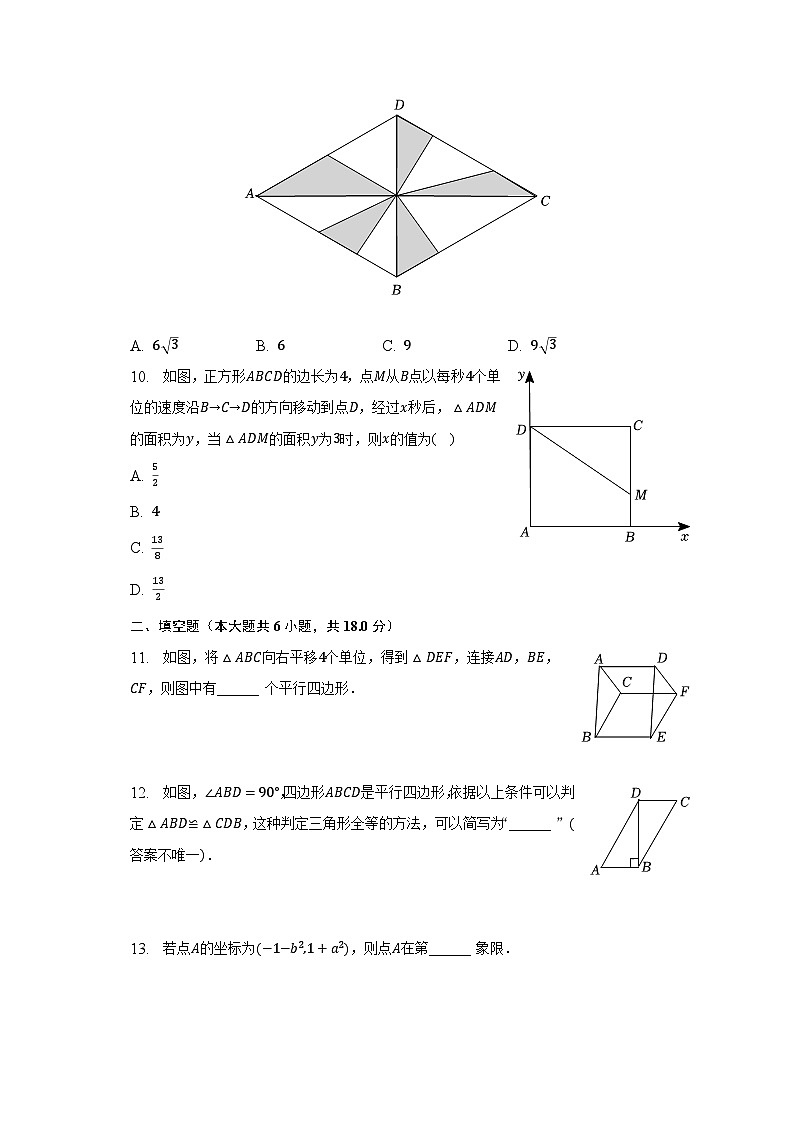
9. 如图，在菱形ABCD中，AC，BD为对角线，BC=6，∠BAD=60°，则阴影部分的面积为(    )

A. 6 3 B. 6 C. 9 D. 9 3
10. 如图，正方形ABCD的边长为4，点M从B点以每秒4个单位的速度沿B→C→D的方向移动到点D，经过x秒后，△ADM的面积为y，当△ADM的面积y为3时，则x的值为(    )
A. 52
B. 4
C. 138
D. 132
二、填空题（本大题共6小题，共18.0分）
11. 如图，将△ABC向右平移4个单位，得到△DEF，连接AD，BE，CF，则图中有______ 个平行四边形．


12. 如图，∠ABD=90°，四边形ABCD是平行四边形，依据以上条件可以判定△ABD≌△CDB，这种判定三角形全等的方法，可以简写为“______ ”(答案不唯一)．


13. 若点A的坐标为(−1−b2,1+a2)，则点A在第______ 象限．
14. 如图，在△ABC中，∠A=90°，∠C=30°，BD平分∠ABC，过点D作DE⊥BC，垂足为点E，若BC=12，则△DEB的面积为______ ．


15. 小胜参加2023年的高考，到达考点时发现没有带身份证，求助交警后，交警驱车载小胜迅速回到离考点2千米的家取身份证，并立即返回考场，小胜离考点行驶路程y(米)与时间x(分钟)之间的变化关系如图所示，根据图象中的数据，写出y与x(0≤x≤6)之间的函数表达式______ ．


16. 如图，直角边长为单位1的等腰Rt△AOB的直角边OA与x轴重合，以斜边OB的长度为半径画弧，交x轴于点A1，以OA1为直角边的Rt△A1OB1中∠OA1B1=90°，另一直角边A1B1为单位1；以斜边OB1的长度画弧交x轴于点A2，以OA2为直角边的Rt△A2OB2中∠OA2B2=90°，另一直角边A2B2为单位1；以斜边OB2的长度画弧交x轴于点A3，以OA3为直角边的Rt△A3OB3中∠OA3B3=90°，另一直角边A3B3为单位1，依此类推，则Bn的坐标为______ ．

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
如图，在公路与铁路的夹角内部区域，需要建一个货运站点P，使货运站点P到公路和铁路的距离相等，且到公交A站与地铁B站的距离也相等，请用尺规作图在图中标出货运站点P的位置.(不写作法，保留作图痕迹)

18. (本小题6.0分)
如图，在△ABC中，E、F分别是边AB、AC上的点，且EF/​/BC，DF/​/AB，CE平分∠ACB；求证：BD=CF．

19. (本小题6.0分)
如图，在平面直角坐标系中，△ABC的顶点都在网格点上，其中C的坐标为(1,2)．
(1)点A的坐标是______ ，点B的坐标是______
(2)将△ABC绕A点顺时针旋转90°，得到Δ A′B′C′，再将Δ A′B′C′向上平移6个单位得到Δ A″B″C″请在网格直角坐标中画出Δ A″B″C”．
(3)求△ABC的面积．

20. (本小题8.0分)
如图，在△ABC中，AB=AC，点D为△ABC内一点，连接AD，EH⊥AD，E，F，G，H分别是AB，BD，CD，AC的中点，BC=4，AD=6，求：四边形EFGH的面积．

21. (本小题8.0分)
小唐同学去年暑假随爸爸去成都大熊猫繁殖基地看熊猫，发现整个基地的燃猫都未出熊猫内室，当天的温度有33度，他了解到熊猫的外出活动与室外温度有关，因此通过一年(以365天计算)的观察，对熊猫“花花”外出活动时的温度(以0°C至40°C为监测温度区间)进行了调查，并制作了如图所示的频数分布表与直方图：
温度区间温度区间°
频数(天数)
频率
0≤x