

2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷(含解析)
展开2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
1. 能与 8合并的二次根式是( )
A. 12 B. 18 C. 24 D. 28
2. 在正比例函数y=−13x图象上的点是( )
A. (−1,−3) B. (−3,−1) C. (−1,3) D. (−3,1)
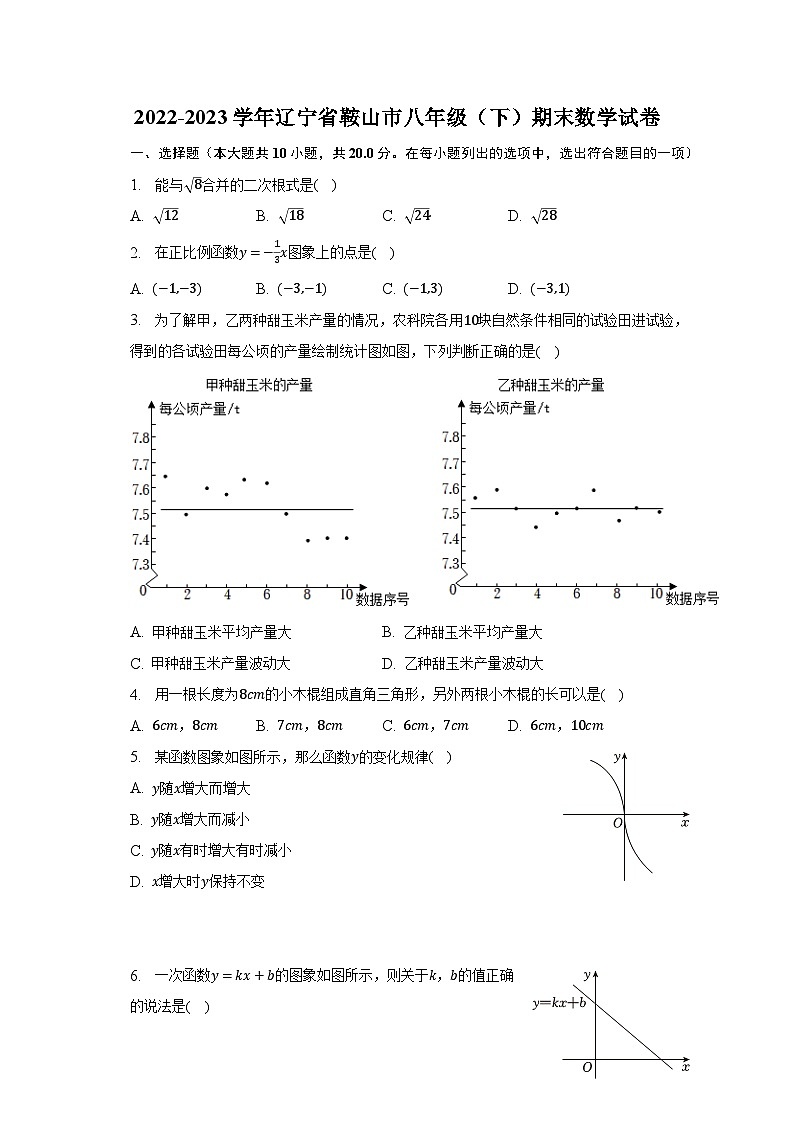
3. 为了解甲,乙两种甜玉米产量的情况,农科院各用10块自然条件相同的试验田进试验,得到的各试验田每公顷的产量绘制统计图如图,下列判断正确的是( )
A. 甲种甜玉米平均产量大 B. 乙种甜玉米平均产量大
C. 甲种甜玉米产量波动大 D. 乙种甜玉米产量波动大
4. 用一根长度为8cm的小木棍组成直角三角形,另外两根小木棍的长可以是( )
A. 6cm,8cm B. 7cm,8cm C. 6cm,7cm D. 6cm,10cm
5. 某函数图象如图所示,那么函数y的变化规律( )
A. y随x增大而增大
B. y随x增大而减小
C. y随x有时增大有时减小
D. x增大时y保持不变
6. 一次函数y=kx+b的图象如图所示,则关于k,b的值正确的说法是( )
A. k>0,b>0
B. k<0,b<0
C. k>0,b<0
D. k<0,b>0
7. 如图,在▱ABCD中,点E,F分别在边AB,CD上,且BE=DF,连接EF与AC交于点O,则下列结论:①OA=OC;②OE=OF;③AC=EF,其中正确结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
8. 如图,学校在校园围墙边缘开垦一块四边形菜地ABCD,测得AB=9m,BC=12m,CD=8m,AD=17m,且∠ABC=90°,这块菜地的面积是( )
A. 48m2 B. 114m2 C. 122m2 D. 158m2
9. 如图,△ABC中,点M,N分别是边AB,AC上的点,且MN//BC,将△ABC沿MN翻折,使点A的对称点A′落在BC边上,若AB=4.6cm,AC=4cm,BC=4.2cm,则△A′MN的周长是( )
A. 6.4cm
B. 8.5cm
C. 8.8cm
D. 12.8cm
10. 游泳池设有浅水区及深水区两个不同区域,其横截面如图所示,游泳馆每次向空池注水的速度相同,注水时水的深度随时间的变化而变化,用函数图象刻画这种变化正确的是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15.0分)
11. 二次根式 2a+1有意义,则a的取值范围是______ .
12. 矩形的边长分别为2和2 3,两条对角线相交所形成的夹角中,锐角的度数是______ .
13. 某销售公司招聘一名项目经理,甲,乙,丙三人最后考核成绩如表:公司决定笔试成绩,面试成绩与计算机操作成绩分别按3:5:2,计算平均成绩,那么应聘者______ 会被录取.
应试者
笔试成绩
面试成绩
计算机操作
甲
88
90
90
乙
92
85
90
丙
90
94
88
14. 如图,由边长为1个单位长度的小正方形组成的网格中,点A,B,C都在小正方形的格点上,则∠ABC的度数是______ .
15. 如图,河的两岸有A,B两个水文观测点,为方便联络,要在河上修一座木桥MN(河的两岸互相平行,MN垂直于河岸),现测得A,B两点到河岸的距离分别是5米,4米,河宽3米,且A,B两点之间的水平距离为12米,则AM+MN+NB的最小值是______ 米.
三、解答题(本大题共8小题,共65.0分。解答应写出文字说明,证明过程或演算步骤)
16. (本小题6.0分)
计算:( 2+ 3)2−(2 5+ 6)(2 5− 6).
17. (本小题6.0分)
已知 6≈2.449,求 23−13 24+ 1.5的近似值.(结果保留小数点后两位)
18. (本小题8.0分)
如图,直线y=x+2与x轴,y轴分别交于A,B两点,点C的坐标是(0,−4),点D在x轴正半轴上,且OD=12OC,直线CD交直线AB于点E.
求:(1)△ABC的面积;
(2)点E的坐标.
19. (本小题7.0分)
已知,BD为矩形ABCD的对角线,完成如下操作,并解决问题.
(1)作BD的垂直平分线l;(不写画法,保留作图痕迹)
(2)在直线l上确定两点M,N,使四边形BMDN为正方形,简要阐述作法,并说明理由.
20. (本小题8.0分)
完成表格,在坐标系中画出函数y=x+1x+1(x>0)的图象,根据图象回答问题:观察直线y1=3x(x≥0)的图象,当x取何值时y1>y?
x
…
14
12
1
2
4
…
y
…
3
…
21. (本小题10.0分)
每年6月5日为世界环境日,某中学为增强学生的环保意识,开展了关于保护环境的知识竞赛,经过班级推荐,共有50名学生参赛,其成绩统计如表:
成绩(单位:分)
50
2
8
12
16
12
其中80
(2)根据表格估计此次竞赛成绩的平均数;
(3)根据数据,请写出两条可以获得的信息.
22. (本小题10.0分)
高速公路上A,B两地相距760千米,一辆货车从A地开往B地,同时一辆客车从B开往A地,已知货车的行驶速度为每小时90千米,客车的行驶速度为每小时100千米.设货车与B地的距离为y1(单位:千米),客车与B地的距离为y2(单位:千米);
(1)分别写出y1,y2与出发时间x的函数关系式;
(2)若距离B地400千米处有一服务区,两车均需要在此处加油和休息,请判断两是否会同时进入服务区,并说明理由.
23. (本小题10.0分)
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,AC=2,点D是BC边中点,连接AD,过点B作BE//AD,过点A作AE//BC;
(1)判断四边形ADBE的形状,并证明结论;
(2)点M是线段BE上的动点,点N是线段AC上的动点,且BM=AN,连接MN交AD于点P,若四边形BMPD是平行四边形时,求BM的值,并计算此时MN的长度.
答案和解析
1.【答案】B
【解析】解: 8= 4×2=2 2,
A、 12= 4×3=2 3,不能与 8合并,不符合题意;
B、 18= 9×2=3 2,能与 8合并,符合题意;
C、 24= 4×6=2 6,不能与 8合并,不符合题意;
D、 28= 4×7=2 7,不能与 8合并,不符合题意;
故选:B.
根据二次根式的性质把各个二次根式化简,根据同类二次根式的概念判断即可.
本题考查的是同类二次根式的概念、二次根式的性质,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.
2.【答案】D
【解析】解:y=−13x,
A.x=−1,y=13,不符合题意;
B.x=−3,y=1,不合题意;
C.x=−1,y=13,不符合题意;
D.x=−3,y=1,合题意.
故选:D.
根据y=−13x,所以只要代入点的横坐标与纵坐标就可判断.
本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.
3.【答案】C
【解析】解:从图中看到,甲,乙两种甜玉米平均产量相近,甲种甜玉米产量的波动比乙的波动大.
故选:C.
据从图中数据的波动情况分析.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4.【答案】D
【解析】解:A、∵62+82≠82,故不符合题意;
B、∵72+82≠82,故不符合题意;
C、∵62+72≠82,故不符合题意;
D、∵62+82=102,故符合题意;
故选:D.
根据勾股定理判断即可.
本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
5.【答案】B
【解析】解:由函数图象可知,函数y的变化规律为y随x增大而减小.
故选:B.
根据函数图象判断即可.
本题考查了函数的图象,利用掌握数形结合的方法是解答本题的关键.
6.【答案】D
【解析】解:根据图象随着x的增大而减小,可知k<0,
∵图象与y轴的交点大于0,
∴b>0,
综上可知,k<0,b>0.
故选:D.
根据一次函数的图象与性质之间的关系进行判断.
本题考查了一次函数的图象与性质之间的关系,掌握一次函数的图象与性质之间的关系是关键.
7.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∵AB//CD,AB=CD,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∵BE=DF,
∴AB−BE=CD−DF,
∴AE=CF,
在△AEO和△CFO中,
∠EAO=∠FCOAE=CF∠AEO=∠CFO,
∴△AEO≌△CFO(ASA),
∴OA=OC,OE=OF,
∴①和②正确;
∵AC与EF不一定相等,
∴③不一定正确,
∴正确的距离个数为2,
故选:C.
根据ASA证明△AEO≌△CFO即可判断①、②正确,不能判定③正确.
本题考查了平行四边形的性质,全等三角形的判定与性质,正确得出△AEO≌△CFO是解题的关键.
8.【答案】B
【解析】解:连接AC,
∵∠ABC=90°,AB=9m,BC=12m,
∴AC= AB2+BC2= 92+122=15(m),
∵CD=8m,AD=17m,
∴AC2+CD2=152+82=289,AD2=172=289,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴∠ACD=90°,
∴四边形ABCD的面积=△ABC的面积+△ACD的面积
=12AB⋅BC+12AC⋅CD
=12×9×12+12×15×8
=54+60
=114(m2),
∴这块菜地的面积为114m2,
故选:B.
连接AC,先在Rt△ABC中,利用勾股定理求出AC的长,然后利用勾股定理的逆定理证明△ACD是直角三角形,从而可得∠ACD=90°,最后根据四边形ABCD的面积=△ABC的面积+△ACD的面积,进行计算即可解答.
本题考查了勾股定理的逆定理,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
9.【答案】A
【解析】解:连接AA′交MN于点G,
∵△A′MN由△AM翻折而成,AB=4.6cm,AC=4cm,BC=4.2cm,
∴MN是线段AA′的垂直平分线,
∵MN//BC,
∴MG是△ABA′的中位线,
∴MN是△ABC的中位线,
∴AM=A′M=12AB=2.3cm,AN=A′N=12AC=2cm,MN=12BC=2.1cm,
∴△A′MN的周长=A′M+A′N+MN=2.3+2+2.1=6.4(cm).
故选:A.
连接AA′,根据轴对称的性质可知MN是线段AA′的垂直平分线,再由MN//BC可知MN是△ABC的中位线,据此可得出结论.
本题考查的是翻折变换及平行线的性质,熟知图形翻折不变性的性质是解题的关键.
10.【答案】C
【解析】解:根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢.
故选:C.
首先看图可知,蓄水池的下部分比上部分的体积小,故h与t的关系变化为先快后慢.
本题考查根据几何图形的性质,确定函数的图象和函数图象的作图能力.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.
11.【答案】a≥−12
【解析】解:由题意得:2a+1≥0,
解得:a≥−12,
故答案为:a≥−12.
根据二次根式的被开方数是非负数列出不等式,解不等式得到答案.
本题考查的是二次根式有意义的条件,熟记二次根式的被开方数是非负数是解题的关键.
12.【答案】60°
【解析】解:如图,
∵AB=2,BC=2 3,
∴AC= AB2+BC2= 4+12=4,
∵四边形ABCD是矩形,
∴AO=CO=2=BO=DO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
故答案为:60°.
由勾股定理可求AC的长,由矩形的性质可得AO=CO=2=BO=DO,可证△ABO是等边三角形,可得∠AOB=60°,即可求解.
本题考查了矩形的性质,等边三角形的判定和性质,证明△ABO是等边三角形是解题的关键.
13.【答案】丙
【解析】解:甲的平均成绩为88×3+90×5+90×23+5+2=89.4,
乙的平均成绩为90×3+85×5+90×23+5+2=87.5,
丙的平均成绩为90×3+94×5+88×23+5+2=91.6,
∵91.6>89.4>87.5,
∴应聘者丙会被录取,
故答案为:丙.
根据加权平均数的定义求解即可.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
14.【答案】90°
【解析】解:∵AB2=12+22=5,BC2=22+42=20,AC2=32+42=25,
∴AB2+BC2=AC2,
∴∠ABC=90°,
故答案为:90°.
根据勾股定理及勾股定理逆定理求解即可.
此题考查了勾股定理逆定理、勾股定理,熟记勾股定理逆定理、勾股定理是解题的关键.
15.【答案】18
【解析】解:过点A作AP⊥FG,垂足为P,在AP上截取AH=MN=3米,连接HB交DE于点N,过点N作NM⊥FG,垂足为M,过点B作BC⊥AP,交AP的延长线于点C,交DE于点Q,
由题意得:AH=MN,AH//MN,
∴四边形AHNM是平行四边形,
∴AM=HN,
∴AM+BN=HN+BN=HB,
此时AM+BN的值最小,且最小值即为HB的长,
在Rt△HBC中,BC=12米,HC=AC−AH=5+3+4−3=9(米),
∴HB= BC2+HC2= 122+92=15(米),
∴AM+BN的最小值为15米,
∴AM+MN+NB的最小值=15+3=18米,
故答案为:18.
过点A作AP⊥FG,垂足为P,在AP上截取AH=MN=3米,连接HB交DE于点N,过点N作NM⊥FG,垂足为M,过点B作BC⊥AP,交AP的延长线于点C,交DE于点Q,根据题意可得:AH=MN,AH//MN,从而可得四边形AHNM是平行四边形,进而可得AM=HN,然后根据两点之间,线段最短可得此时AM+BN的值最小,且最小值即为HB的长,最后在Rt△HBC中,利用勾股定理求出HB的长,从而进行计算即可解答.
本题考查了勾股定理的应用,平行四边形的判定与性质,轴对称−最短路线问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
16.【答案】解:( 2+ 3)2−(2 5+ 6)(2 5− 6)
=2+2 6+3−(20−6)
=2+2 6+3−14
=−9+2 6.
【解析】先根据完全平方公式,平方差公式和二次根式的性质进行计算,再关键二次根式的加减法法则进行计算即可.
本题考查了二次根式的混合运算和乘法公式,能正确根据二次根式的运算法则进行计算是解此题的关键.
17.【答案】解:∵ 6≈2.449,
∴ 23−13 24+ 1.5
= 63−2 63+ 32
=− 63+ 62
= 66
≈2.4496
≈0.41.
【解析】结合已知条件,将原式计算后代入数值计算即可.
本题考查无理数的估算及二次根式的计算,特别注意最终结果需保留两位小数.
18.【答案】解:(1)∵直线y=x+2与x轴,y轴分别交于A,B两点,
∴将x=0代入,得y=2,
∴B(0,2),
将y=0代入,得0=x+2,解得x=−2,
∴A(−2,0),
∴OA=2,
∵点C的坐标是(0,−4),
∴BC=2−(−4)=6,
S△ABC=12BC⋅OA=12×6×2=6;
(2)∵点C的坐标是(0,−4),OD=12OC,
∴D(2,0),
设直线CD的解析式为y=kx+b,将C(0,−4),D(2,0)代入得,
b=−42k+b=0,解得b=−4k=2,
∴直线CD的解析式为y=2x−4,
∵直线CD交直线AB于点E,
∴y=x+2y=2x−4,解得x=6y=8,
∴E(6,8).
【解析】(1)根据已知条件求点A和点B的坐标,结合点C的坐标,求出BC和OA的长度,即可求△ABC的面积;
(2)已知点C的坐标,由OD=12OC,可求点D的坐标,用待定系数法求直线CD的解析式,与直线y=x+2联立,解方程组即可求出点E的坐标.
本题考查了用待定系数法求一次函数关系式,直线与坐标轴围成的图形的面积,掌握待定系数法求解析式及联立方程求交点坐标是解题的关键.
19.【答案】解:(1)如图:
直线l即为所求;
(2)设直线l交BD于O,则O为BD中点,如上图:
以O为圆心,OB为半径作⊙O交直线l于M,N,连接MB,MD,NB,BD,
四边形BMDN即为所求;
理由如下:
由作图可知,OB=OM=OD=ON,
∴四边形BMDN是平行四边形,且MN=BD,
∴四边形BMDN是矩形,
∵直线l是BD的垂直平分线,
∴MB=MD,
∴四边形BMDN是正方形.
【解析】(1)根据垂直平分线的尺规作图步骤作图即可;
(2)设直线l交BD于O,以O为圆心,OB为半径作⊙O交直线l于M,N,四边形BMDN即为所求.
本题考查作图−复杂作图,解题的关键是掌握尺规作垂直平分线和正方形的判定定理.
20.【答案】解:完成表格如下:
x
…
14
12
1
2
4
…
y
…
214
72
3
72
214
…
图象如图:
根据图象可得:当x>1时y1>y.
【解析】将x的值代入函数表达式,即可求解;然后描点画出函数图象,根据图象即可得到结论;
本题考查函数的图象与性质,观察函数图象并结合函数性质是解决本题的关键.
21.【答案】解:(1)此次竞赛成绩的中位数为第25个和第26个数据的平均数,
所以中位数为82+822=82;
(2)55×2+65×8+75×12+85×16+95×1250=80.6(分),
答:估计此次竞赛成绩的平均数为80.6分;
(3)①90分以上有12人,占总人数的1250=24%,
②有2人成绩小于或等于60分,应加强学生的环保意识.(答案不唯一,只要言之有理均可).
【解析】(1)根据中位数的定义进行计算;
(2)根据平均数的定义进行计算;
(3)分析表格,获得相应的信息.
本题考查频数分布表、中位数、加权平均数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.【答案】解:(1)设行驶时间为x小时,则y1和y2的表达式为:
y1=760−90x(0≤x≤769h)y2=100x(0≤x≤769h);
(2)假设客车和火车同时进入服务区,即y1=y2,
即760−90x=100x,
解得:x=4h,取值符合题意,
此时代入y表达式得:y=400km,所以客车和货车同时进入服务区,
【解析】(1)通过题干的定义求出客车和货车距离B地的函数表达式;
(2)将相遇问题转化为一次函数相交问题求解,注意时间x的取值范围.
本题主要考查一次函数的应用,理解题意,根据题意列出解析式是解题的关键.
23.【答案】(1)证明:四边形ADBE是菱形,理由如下:
∵BE//AD,AE//BC,
∴四边形ADBE是平行四边形,
又∵Rt△ABC中,∠BAC=90°,点D是BC边中点,
∴AD=BD=CD=12BC,
∴四边形ADBE是菱形;
(2)解:∵在Rt△ABC中,∠BAC=90°,∠ABC=30°,AC=2,点D是BC边中点,
∴AD=BD=CD=12BC=2=AC,
∵四边形BMPD是平行四边形,
∴PM//BC,BM=DP,
在正三角形ACD中,
∵PN//BC,
∴△ANP是正三角形,
∴AN=AP=PN,
∵BM=AN,
∴AP=PD=PN=BM=1,
∴MN=MP+PN=2+1=3,
答:BM=1,MN=3.
【解析】(1)根据两组对边分别平行证明四边形ADBE平行四边形,再由邻边相等的四边形是菱形得以证明;
(2)根据直角三角形的斜边中线等于斜边一半得出AD=BD=CD=12BC=2=AC,进而得到△ACD是正三角形,由四边形BMPD是平行四边形,得出AN=AP=BM=PD=1,再根据平行四边形的性质求出MN即可.
本题考查直角三角形的性质,正三角形,平行四边形的性质和判定,菱形,掌握直角三角形斜边中线等于斜边一半,正三角形的性质以及平行四边形、菱形的性质和判定是正确解答的前提.
2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷(含答案解析),共15页。试卷主要包含了能与 8合并的二次根式是等内容,欢迎下载使用。
2022-2023学年辽宁省鞍山市千山区八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年辽宁省鞍山市千山区八年级(下)期中数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年辽宁省鞍山市八年级(下)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












