河南省周口市西华县2022-2023学年八年级下学期期末数学试题（含答案）

2022－2023学年下期期末调研八年级试卷

数学

注意事项：

1．本试卷共6页，三个大题，满分120分，考试时间100分钟．

2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上．答在试卷上的答案无效．

一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的．

1．下列二次根式是最简二次根式的是（）

A． B． C． D．

2．下列函数中，y是x的正比例函数的是（）

A． B．y＝2x＋1 C． D．y＝x²

3．下列计算正确的是（）

A． B． C． D．

4．小明在计算一组数据的方差时，列出的算式如下：，根据算式信息，下列判断错误的是（）

A．平均数是8 B．极差是2 C．众数是8 D．中位数是8

5．一直角三角形的两边长分别为6和8，则第三边的长为（）

A．10 B． C． D．10或

6．在数学课上，为探究四边形瓷砖是否为菱形，以下拟定的测量方案，正确的是（）

A．测量四个内角是否相等  B．测量两条对角线是否互相垂直

C．测量一组对边是否平行且相等 D．测量四条边是否相等

7．关于一次函数y＝2x＋3的描述，下列说法正确的是（）

A．图象经过第一、三、四象限 B．图象与x轴的交点坐标为（0，3）

C．图象沿y轴向下平移3个单位，可得到y＝2x D．当x＜0时，y＜0

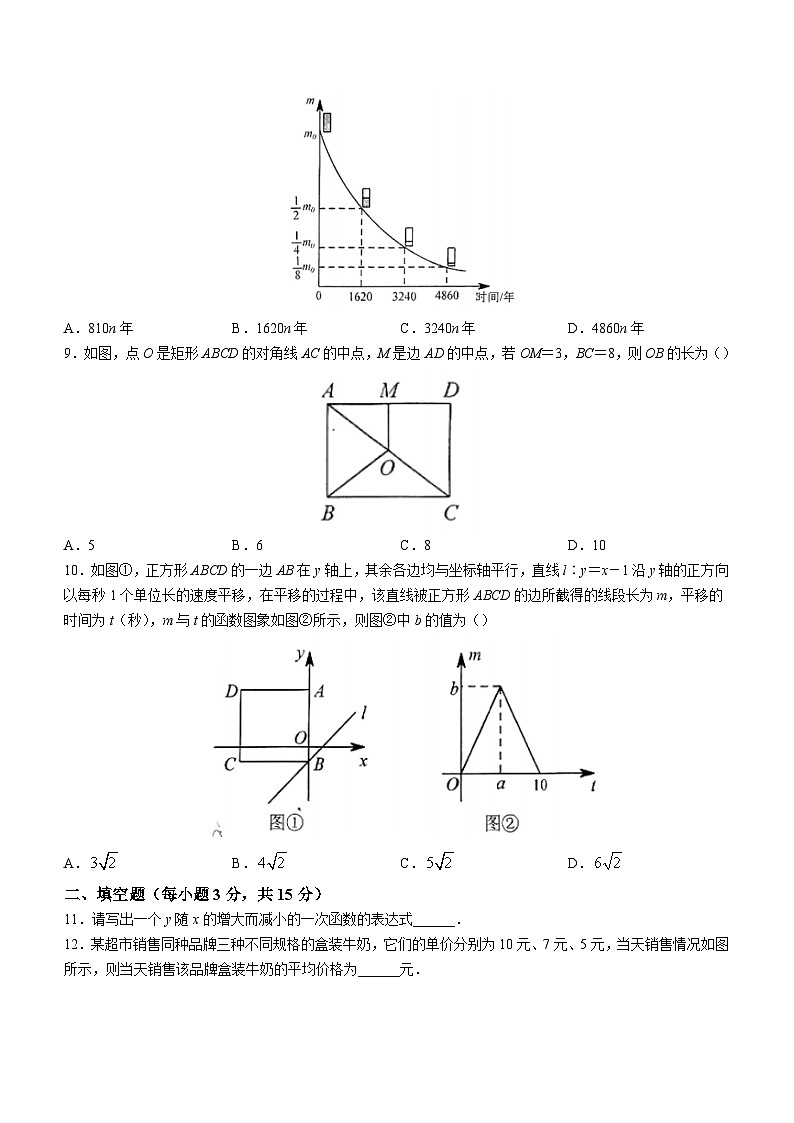
8．1903年，英国物理学家卢瑟福通过实验证实，放射性物质在放出射线后，这种物质的质量将减少，减少的速度开始较快，后来较慢．实际上，放射性物质的质量减为原来的一半所用的时间是一个不变的量，我们把这个时间称为此种放射性物质的半衰期．如图是表示镭的放射规律的函数图象，根据图象可以判断，镭的质量衰减到（n为正整数）的时间是（）

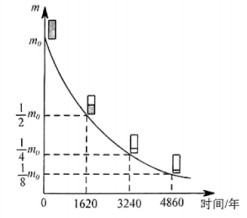
A．810n年 B．1620n年 C．3240n年 D．4860n年

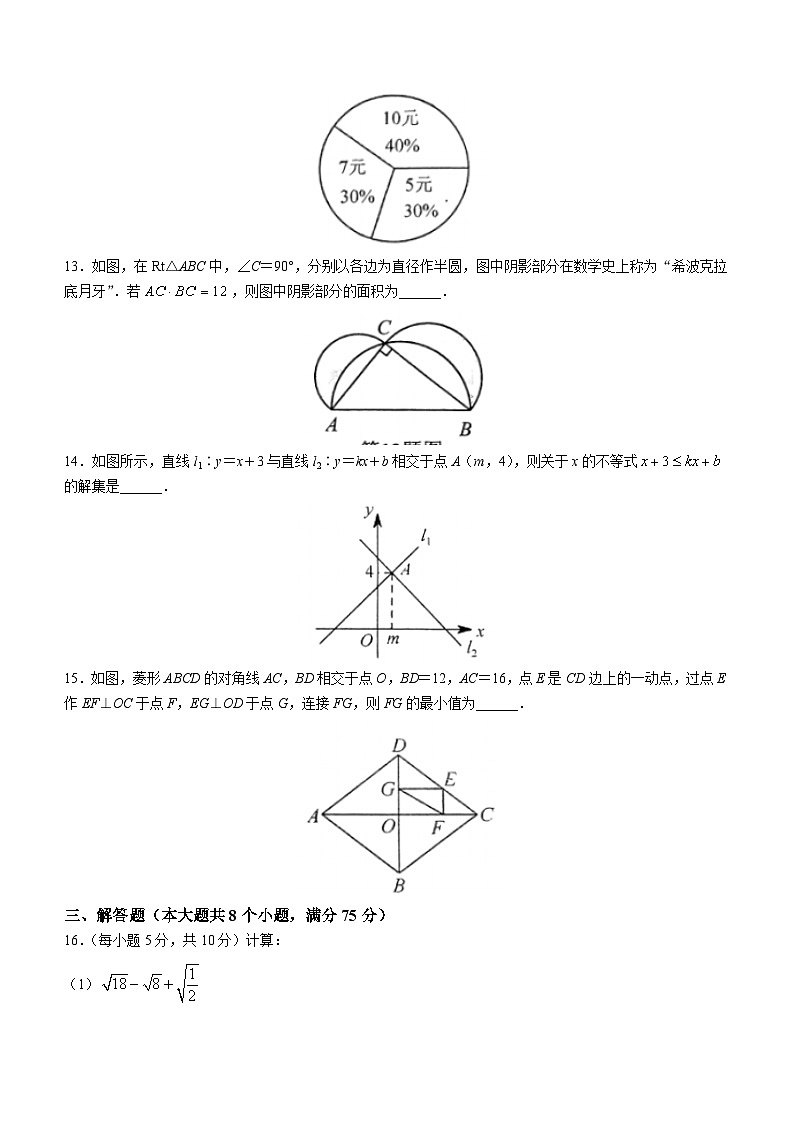
9．如图，点O是矩形ABCD的对角线AC的中点，M是边AD的中点，若OM＝3，BC＝8，则OB的长为（）

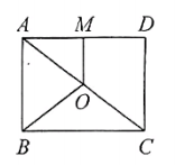
A．5 B．6 C．8 D．10

10．如图①，正方形ABCD的一边AB在y轴上，其余各边均与坐标轴平行，直线l∶y＝x－1沿y轴的正方向以每秒1个单位长的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图②所示，则图②中b的值为（）

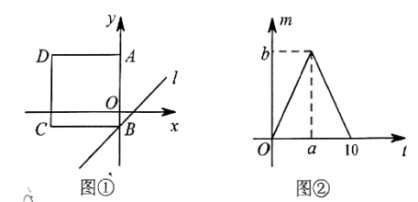
A． B． C． D．

二、填空题（每小题3分，共15分）

11．请写出一个y随x的增大而减小的一次函数的表达式______．

12．某超市销售同种品牌三种不同规格的盒装牛奶，它们的单价分别为10元、7元、5元，当天销售情况如图所示，则当天销售该品牌盒装牛奶的平均价格为______元．

13．如图，在Rt△ABC中，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”．若，则图中阴影部分的面积为______．

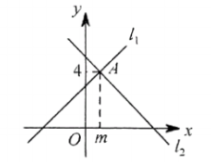
14．如图所示，直线l1∶y＝x＋3与直线l2∶y＝kx＋b相交于点A（m，4），则关于x的不等式的解集是______．

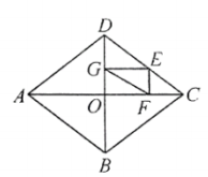
15．如图，菱形ABCD的对角线AC，BD相交于点O，BD＝12，AC＝16，点E是CD边上的一动点，过点E作EF⊥OC于点F，EG⊥OD于点G，连接FG，则FG的最小值为______．

三、解答题（本大题共8个小题，满分75分）

16．（每小题5分，共10分）计算：

（1）

（2）

17．（9分）下面是小明同学设计的“已知一组邻边构造平行四边形”的尺规作图过程．

已知：如图，线段AB，BC．求作：平行四边形ABCD．

作法：①分别以A、C为圆心，BC、AB的长为半径画弧，两弧交于点D；

②连接AD，CD．四边形ABCD即为所求作的平行四边形．

（1）请你使用直尺和圆规，帮助小明补全尺规作图过程（保留作图痕迹）；

（2）证明上述作法所得的四边形ABCD是平行四边形．

18．（9分）2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课，这是中国空间站的第二次太空授课，被许多中小学生称为“最牛网课”．某中学为了解学生对“航空航天知识”的掌握情况，随机抽取50名学生进行测试，并对成绩（百分制）进行整理，信息如下：

a．成绩频数分布表：

b．这一组的成绩是（单位：分）：

70  71  72  72  74  77  78  78  79  79  79  79

根据以上信息，回答下列问题：

（1）在这次测试中，成绩的中位数是______分，成绩不低于80分的人数占测试人数的百分比为______．

（2）这次测试成绩的平均数是76.4分，甲的测试成绩是77分．乙说：“甲的成绩高于平均数，所以甲的成绩高于一半学生的成绩．”你认为乙的说法正确吗？请说明理由．

（3）请对该校学生“航空航天知识”的掌握情况作出合理的评价．

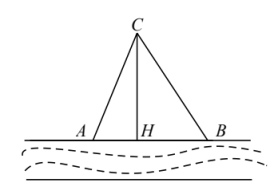
19．（9分）如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A、B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村庄为方便村民取水，决定在河边新建一个取水点H（A、B、H在同一直线上），并新建一条路CH，测得千米，CH＝3千米，HB＝2千米．

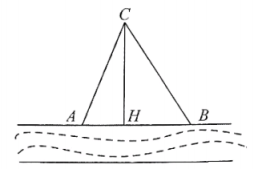
（1）CH是不是从村庄C到河边的最近路？请通过计算加以说明；

（2）新路CH比原路AC短多少千米？

20．（9分）如图，在四边形ABCD中，，对角线BD的垂直平分线与边AD，BC分别相交于点M，N，连接BM，DN．

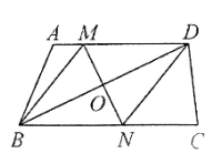
（1）求证：四边形BNDM是菱形；

（2）若BD＝24，BM＝13，求菱形BNDM的面积．

21．（9分）已知直线与x轴、y轴分别交于点A、点B．

（1）求A、B两点的坐标；

（2）将直线l1向右平移8个单位后得到直线l2，求直线l2的解析式；

（3）设直线l2与x轴的交点为P，求△PAB的面积．

22．（10分）甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BC→CD→DE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系．请根据图象解答下列问题：

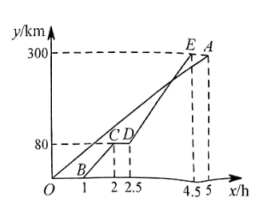
（1）线段CD表示轿车在途中停留了______h．

（2）轿车走折线DE的速度为______km/h．

（3）求轿车从甲地出发后经过多长时间追上货车？

23．（10分）我们可以通过类比联想、引申拓展研究典型题目，以达到触类旁通的目的．下面是一个案例，请补充完整．

原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF＝45°，连接EF，则EF＝BE＋DF，试说明理由．

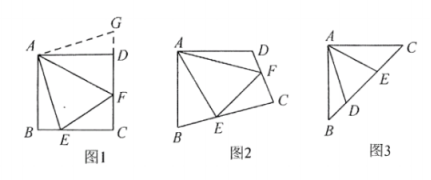
（1）思路梳理

如图1，把△ABE绕点A逆时针旋转90°至△ADG，易知△ADG≌△ABE

∴AG＝AE，BE＝DG，∠DAG＝∠BAE，∠ADG＝∠ABE．

∵四边形ABCD是正方形，∠EAF＝45°，

∴∠FDG＝∠ADF＋∠ADG＝180°，点F，D，G共线；

∠FAG＝∠FAD＋∠DAG＝∠FAD＋∠BAE＝45°＝∠EAF

易得△AEF≌______（），得EF＝GF＝BE＋DF．

（2）类比引申

如图2，四边形ABCD中，AB＝AD，∠BAD＝90°，点E，F分别在边BC，CD上，∠EAF＝45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系______时，仍有EF＝BE＋DF．

（3）联想拓展

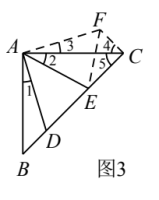
如图3，在△ABC中，∠BAC＝90°，AB＝AC，点D，E均在边BC上，且∠DAE＝45°．

猜想BD，DE，EC应满足的等量关系，并写出推理过程．

2022—2023学年下期期中八年级阶段练习

数学试题参考答案

一、选择题（每小题3分，共30分）

二、填空题（每小题3分，共15分）

三、解答题（本大题共8个小题，共75分）

16．（1）原式

．

（2）原式

＝20－1＋6－9

＝16．

17．（1）如图所示，四边形ABCD即为所求作的平行四边形．

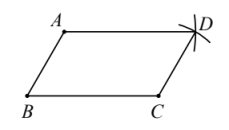
（2）（过程略）

18．（1）78.5，44%．

（2）不正确．因为甲的成绩77分低于中位数78.5分，所以甲的成绩不可能高于一半学生的成绩．

（3）测试成绩不低于80分的人数占测试人数的44%，说明该校学生对“航空航天知识”的掌握情况较好．（注：答案不唯一，合理即可）

19．（1）CH是从村庄C到河边的最近路．理由如下：

∵，∴CH2＋HB2＝CB2．

∴△BCH为直角三角形，∠BHC＝90°，∴CH⊥AB．

∴CH是村庄C到河边的最近路；

（2）设AC＝x千米，则AB＝x千米，AH＝（x－2）千米，

在Rt△ACH中，AH2＋CH2＝AC2即（x－2）2＋32＝x2，

解得即（千米）．

∵（千米），

∴新路CH比原路AC短0.25千米．

20．（1）证明略（2）120（过程略）

21．（1）A（－6，0），B（0，3）（过程略）

（2）∵直线l2是将直线l1向右平移8个单位后得到的，

∴直线l2的解析式为：即．（方法不唯一）

（3）由题可知点P是由点A（－6，0）向右平移8个单位得到的，

∴点P的坐标是（2，0），∴AP＝8，

又B（0，3），∴OB＝3且OB⊥AP

∴．（方法不唯一）

22．（1）0.5   （2）110

（3）①求线段OA的函数解析式

设线段OA的函数解析式为y＝k1x，∵线段OA经过点A（5，300），

∴300＝5k1，解得k1＝60，

∴线段OA的函数解析式为y＝60x．

②求线段DE的函数解析式

设线段DE的函数解析式为y＝k2x＋b，

∵点D（2.5，80），E（4.5，300）在线段DE上，

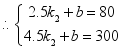解得

∴线段DE的函数解析式为y＝110x－195（）．

联立方程可得，解得x＝3.9

3.9－1＝2.9（）

∴轿车从甲地出发后经过2.9h追上货车

23．（1）△AGF SAS

（2）∠B＋∠D＝180°

（3）DE2＝BD2＋EC2．

（提示：把△ABD绕点A逆时针旋转90°到△ACF的位置，连接EF，如图3所示则△ABD≌△ACF．然后证：①△ADE≌△AFE，②∠ECF＝90°）

（方法不唯一，也可以把△ACE顺时针旋转90°）