初中数学华师大版七年级上册第5章 相交线与平行线5.2 平行线3 平行线的性质教学课件ppt

这是一份初中数学华师大版七年级上册第5章 相交线与平行线5.2 平行线3 平行线的性质教学课件ppt，共18页。PPT课件主要包含了a∥c等内容，欢迎下载使用。

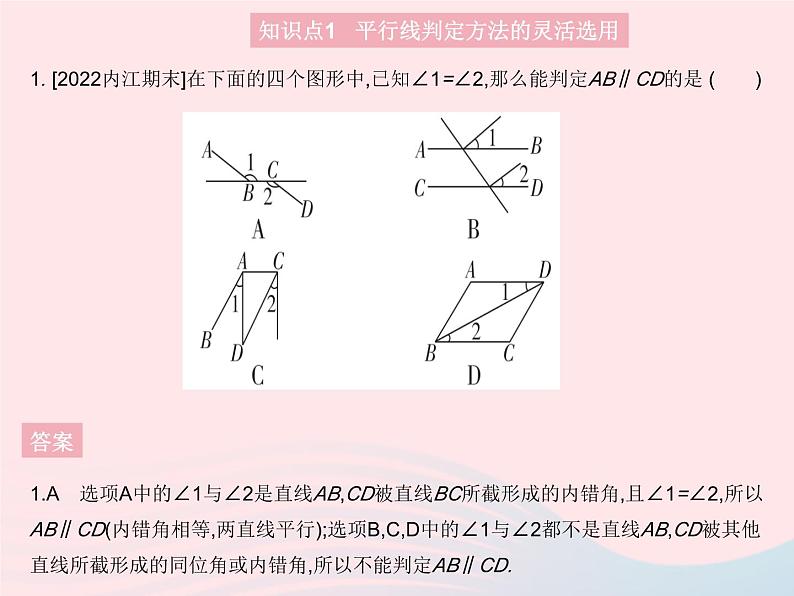
1. [2022内江期末]在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是 (　　)
知识点1 平行线判定方法的灵活选用
1.A　选项A中的∠1与∠2是直线AB,CD被直线BC所截形成的内错角,且∠1=∠2,所以AB∥CD(内错角相等,两直线平行);选项B,C,D中的∠1与∠2都不是直线AB,CD被其他直线所截形成的同位角或内错角,所以不能判定AB∥CD.
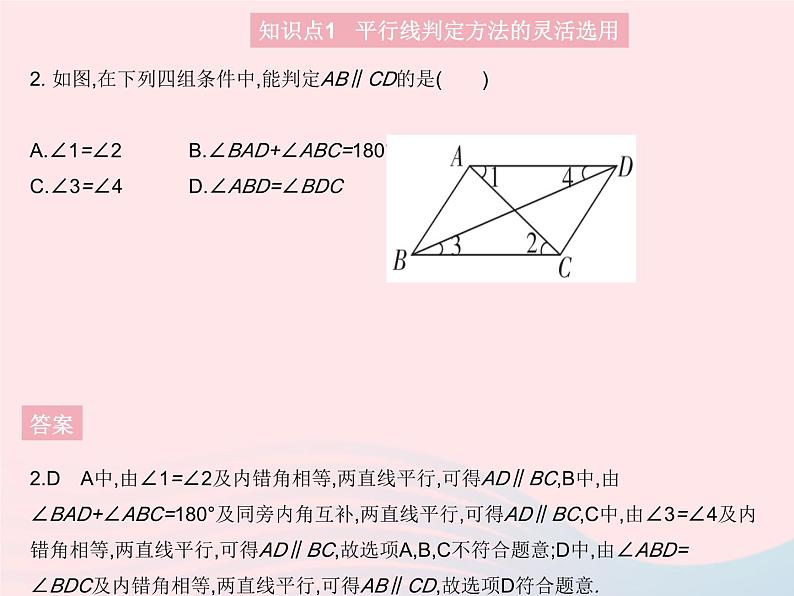
2. 如图,在下列四组条件中,能判定AB∥CD的是(　　)　　　　　　　　　　　　　　　A.∠1=∠2B.∠BAD+∠ABC=180°C.∠3=∠4D.∠ABD=∠BDC
2.D　A中,由∠1=∠2及内错角相等,两直线平行,可得AD∥BC,B中,由∠BAD+∠ABC=180°及同旁内角互补,两直线平行,可得AD∥BC,C中,由∠3=∠4及内错角相等,两直线平行,可得AD∥BC,故选项A,B,C不符合题意;D中,由∠ABD=∠BDC及内错角相等,两直线平行,可得AB∥CD,故选项D符合题意.
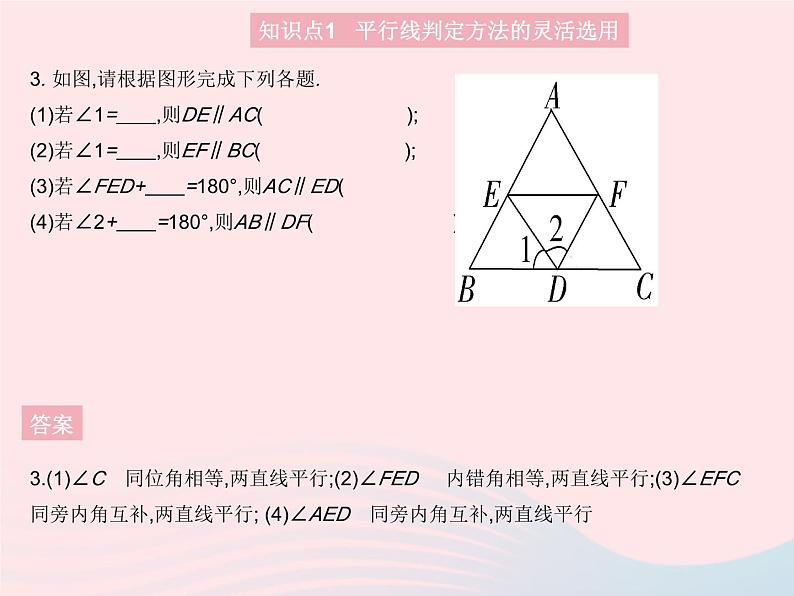
3. 如图,请根据图形完成下列各题.(1)若∠1=　　,则DE∥AC( ); (2)若∠1=　　,则EF∥BC( ); (3)若∠FED+　　=180°,则AC∥ED(　　　　　　　); (4)若∠2+　　=180°,则AB∥DF(　　　　　　　). 
3.(1)∠C　同位角相等,两直线平行;(2)∠FED 内错角相等,两直线平行;(3)∠EFC　同旁内角互补,两直线平行; (4)∠AED　同旁内角互补,两直线平行
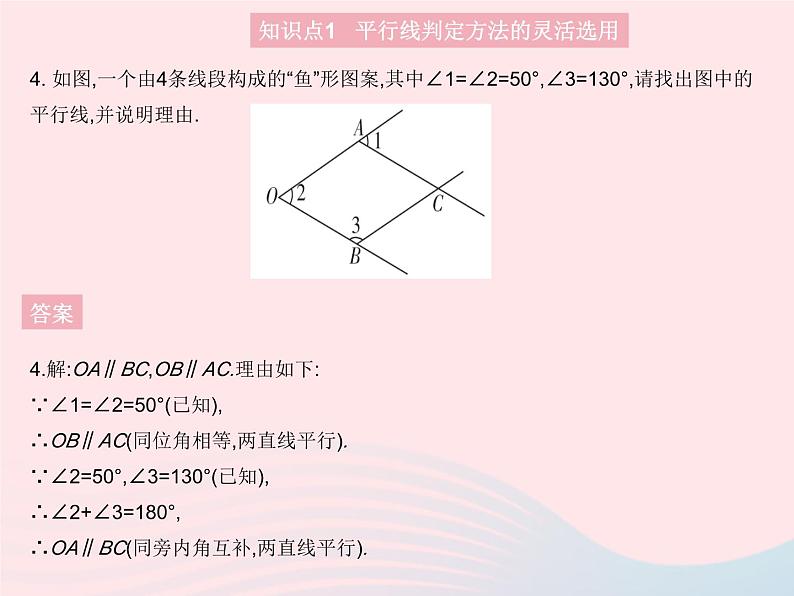
4. 如图,一个由4条线段构成的“鱼”形图案,其中∠1=∠2=50°,∠3=130°,请找出图中的平行线,并说明理由.
4.解:OA∥BC,OB∥AC.理由如下:∵∠1=∠2=50°(已知),∴OB∥AC(同位角相等,两直线平行).∵∠2=50°,∠3=130°(已知),∴∠2+∠3=180°,∴OA∥BC(同旁内角互补,两直线平行).
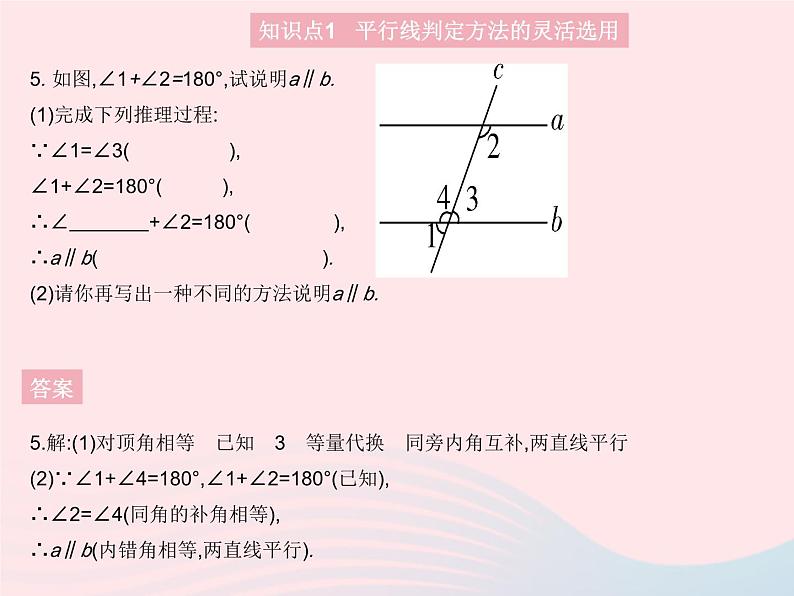
5. 如图,∠1+∠2=180°,试说明a∥b.(1)完成下列推理过程:∵∠1=∠3(　　　　　),∠1+∠2=180°(　　　),∴∠　　　　+∠2=180°( ), ∴a∥b(　　　　　　　　　　　 ).(2)请你再写出一种不同的方法说明a∥b.
5.解:(1)对顶角相等　已知　3　等量代换　同旁内角互补,两直线平行 (2)∵∠1+∠4=180°,∠1+∠2=180°(已知),∴∠2=∠4(同角的补角相等),∴a∥b(内错角相等,两直线平行).
6. 在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是　　　　. 
知识点2 在同一平面内,垂直于同一条直线的两条直线平行
7. 教材P173例3变式“在同一平面内,垂直于同一条直线的两条直线平行”,运用这一性质可以说明铺设铁轨互相平行的道理.如图,已知∠2是直角,再度量出∠1或∠3的度数就会知道铁轨是否平行.方案一:若量得∠3=90°,结合∠2的情况,说明理由.方案二:若量得∠1=90°,结合∠2的情况,说明理由.
7.解:方案一:已知∠2=90°,若量得∠3=90°,则两条铁轨垂直于同一条枕木,所以由在同一平面内,垂直于同一条直线的两条直线平行可得两铁轨平行.方案二同理可得.
1. 某人在广场上练习驾驶汽车,两次拐弯后,汽车行驶方向与原来相同,则这两次拐弯的角度可能是 (　　)　　　　　 　　　　　　　　　　A.第一次右拐50°,第二次右拐130°B.第一次右拐50°,第二次左拐130°C.第一次左拐30°,第二次右拐30°D.第一次左拐50°,第二次左拐120°
1.C　如图(实线为汽车的行驶路线,箭头表示汽车的行驶方向),易知选C.
2. [2022重庆黔江区期末]如图,下列说法错误的是 (　　)A.∵∠1=∠2,∴l3∥l4B.∵∠2+∠5=180°,∴l3∥l4C.∵∠1=∠4,∴l1∥l2D.∵∠1=∠3,∴l1∥l2
2.D　A项,∵∠1=∠2,∴l3∥l4(内错角相等,两直线平行),不符合题意;B项,∵∠2+∠5=180°,∴l3∥l4(同旁内角互补,两直线平行),不符合题意;C项,∵∠1=∠4,∴l1∥l2(内错角相等,两直线平行),不符合题意;D项,由∠1=∠3不能得到l1∥l2,符合题意.
3. [2021洛阳第二外国语学校期中]已知在同一平面内有三条不同的直线a,b,c,下列说法错误的个数是 (　　)①若a∥b,a∥c,则b⊥c;②若b∥a,c∥a,则b∥c;③若b⊥a,c⊥a,则b⊥c. A.1B.2C.3D.0
3.B　若a∥b,a∥c,则b∥c,故①说法错误;若b⊥a,c⊥a,且b,c是两条不同的直线,则b∥c,故③说法错误;易知②说法正确.
4. [2022商丘期中]如图,∠1=120°,∠2=60°,∠3=105°,则∠4=　　　°时,AB∥EF. 
4.105　如图,∵∠1=120°,∠1+∠5=180°,∴∠5=60°.∵∠2=60°,∴∠2=∠5,∴AB∥CD.当∠4=105°时,∵∠3=105°,∴∠3=∠4,∴CD∥EF,∴AB∥EF.
5. 将一副直角三角尺按如图所示的方式放置.(1)①若∠DCE=45°,求∠ACB的度数;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两个三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE的度数的所有可能取值(不必说明理由);若不存在,请说明理由.
5.解:(1)①∵∠ECB=90°,∠DCE=45°,∴∠DCB=90°-45°=45°,∴∠ACB=∠ACD+∠DCB=90°+45°=135°.
②∵∠ACB=140°,∠ACD=90°,∴∠DCB=140°-90°=50°,∴∠DCE=∠ECB-∠DCB=90°-50°=40°.(2)∠ACB+∠DCE=180°.理由如下:∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°.(3)这两个三角尺存在一组边互相平行.当AD∥BC时,∠ACE=30°,当AC∥BE时,∠ACE=45°,当AD∥CE时,∠ACE=120°,当BE∥CD时,∠ACE=135°,当BE∥AD时,∠ACE=165°.综上,∠ACE的可能取值为30°,45°,120°,135°,165°.
素养提升6. 已知直线AB和CD被直线MN所截.(1)如图1,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足什么条件时,AB∥CD?为什么?(2)如图2,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足什么条件时,AB∥CD?为什么?(3)如图3,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD?为什么?