人教版九年级下册26.1.1 反比例函数教学设计

教     学     互     动     设     计

方法

导引

一、新课引入

1、反比例函数的一般形式是 _____________ ，它的图象是 ______________.                             .

2、反比例函数 y= -- 的图像在第__________ 象限，在每个象限内它的图像上y随x的减小而_____________.

3、反比例函数y=  的图像在第___________ 象限，在每个象限内它的图像上y随x的增大而___________.

4、反比例函数经过点（1，－2），这个反比例函数关系式是__________.           .

二、自主探究

认真阅读课本本节的相关内容，完成下面练习并体验知识点的形成过程.

1、用反比例函数解决体积问题

例1  市煤气公司要在地下修建一个容积为的圆柱形煤气储存室．

(1)储存室的底面积S(单位：)与其深度d(单位：m)有怎样的函数关系?

(2)公司决定把储存室的底面积S定为500，施工队施工时应该向下挖进多深?

(3)当施工队按(2)中的计划挖进到地下15m时，碰上了坚硬的岩石，为了节约建设资金，公司临时改变计划把储存室的深改为15m，相应地，储存室的底面积应改为多少才能满足需要(精确0.01 ).

解：（1）根据圆柱体的体积公式，我们有s.d=________,变形得s=__________,即储存室的底面积s是其深度d的___________

函数.

（2）把s=500代入______，得500=______解得d=______如果把储存室的底面积定为500，施工时应向地下掘进______m深.

（3）根据题意，把______代入______，得s=______解得s______.

当储存室的深为15m时，储存室的底面积应改为______才能满足需要.

2、用反比例函数解决工程问题

例2  码头工人以每天30吨的速度往一艘轮船上装载货物，装载完毕恰好用了8天时间.

(1)轮船到达目的地后开始卸货，卸货速度v（单位：吨／天）与卸货时间t（单位：天）之间有怎样的函数关系？

(2)由于遇到紧急情况，船上货物必须在不超过5天内卸载完毕，那么平均每天至少要卸多少吨货物?

分析：根据装货速度 × 装货时间 = 货物的总量，可以求出轮船装载货物的总量；再根据卸货速度 = 货物的总量 ÷ 卸货时间，得到v与t的函数解析式.

解：（1）设轮船上的货物总量为k吨，则根据已知的条件有__________，所以v与t的函数解析式为__________.

（2）把t=5代入_________，得_________从结果可以看出，如果全部货物恰好用5天卸完，则平均每天卸御_________吨，若货物在不超过_________天内卸完，则平均每天至少要卸货_________吨.

复习巩固，并自主探究用反比例函数解决有关实际问题

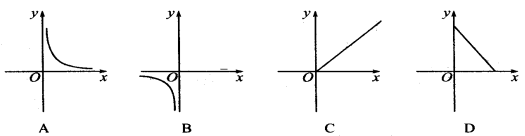
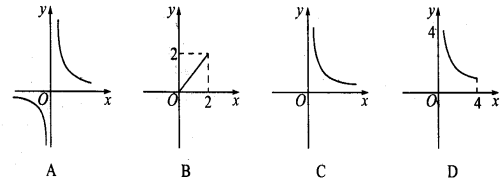
三、课堂练习，巩固新知

1、一个圆柱体的侧面展开图是一个面积为10的矩形，这个圆柱的高h与底面半径r之间的函数关系是（    ）

（A）正比例函数   （B）一次函数  

（C）反比例函数   （D）函数关系不确定

2、已知矩形的面积为10，则它的长y与宽x之间的关系用图象大致可表示为  （    ）

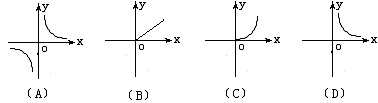
3、面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是（      ）

四、归纳总结

1、长方体中当体积V一定时，高h与底面积S的关系_____________            .

2、在工程问题中，当 __________ 一定时，_____________________                                                                               与____________成反比例_______________________.

3、学习反思：_

  (1)我们建立反比例函数解决实际问题的过程是怎样的？

 （2）在这个过程中要注意什么问题？

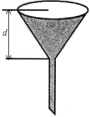
五、课堂作业

1、如图,某玻璃器皿制造公司要制造一种容积为1L（1L=1dm3）的圆锥形漏斗.

(1)漏斗口的面积S（单位: dm2） 与漏斗的深d（单位: dm）有怎样的函数关系?
(2)如果漏斗口的面积为100cm2 ,那么漏斗的深为多少?

2、一司机驾驶汽车从甲地去乙地,他以80km/h 的平均速度，用6小时到达目的地。
(1)当他按原路匀速返回时，汽车的速度v与时间t有怎样的函数关系?
(2)如果该司机必须在4个小时之内回到甲地,那么返程时的速度不能小于多少?

六、课外作业

1、有一面积为60的梯形，其上底长是下底长的   ，若下底长为x，高为y，则y与x的函数关系式为 ________。

2、有x个小朋友平均分20个苹果，每人分得的苹果y（个/人）与x（个）之间的函数是____函数，其函数关系式是_________．当人数增多时，每人分得的苹果就会减少，这正符合函数y＝  （k＞0），当x＞0时，y随x的增大而________的性质。

3、某乡的粮食总产量为a(a为常数)吨，设该乡平均每人占有粮食为y(吨)，人口数为x，则y与x间的函数关系的图象为：(   )

自主归纳总结如何用反比例函数解决有关实际问题并总结应该注意的地方．

学生独立思考并完成，通过练习进一步巩固中心对称的相关知识

通过当堂检测，找到学生自己当堂的问题，并用两种颜色的笔做好修改，注释和笔记等