

人教版九年级下册26.1.1 反比例函数教案设计
展开
这是一份人教版九年级下册26.1.1 反比例函数教案设计,共5页。教案主要包含了复习旧知,新知引入,当堂训练,课堂小结,布置作业,板书设计等内容,欢迎下载使用。
26.1.1反比例函数教学目标1.知识与技能 会识别相关量之间的反比例关系,理解反比例函数的意义,能确定简单的反比例函数关系式. 2.过程与方法 通过对实际问题的分析、类比、归纳,培养学生分析问题的能力,并体会函数在实际问题中的应用. 3.情感、态度与价值观 让学生体会数学来源于生活,又能为社会服务,在实际问题的分析中感受数学美.教学重点 :理解反比例函数的意义,确定反比例函数的解析式难点:反比例函数的解析式的确定教学方法:自主、合作、探究教学用具:多媒体教学过程:一、复习旧知1.在一个变化的过程中,如果有两个变量x和y,当x在其取值范围内任意取一个值时, y 都有唯一确定的值与之对应 ,则称x为 自变量 ,y叫x的 函数 .2.一次函数的解析式是: y=kx+b ;当 b=0 时,称为正比例函数.3.一条直线经过点(2,3)、(4,7),则该直线的解析式为. y=2x-1 这种求函数解析式的方法叫: 待定系数法 . 二、新知引入师:提出问题,让学生先独立思考完成,再合作交流,经历探索反比例函数意义的过程。下列问题中,变量间的对应关系可用怎样的函数关系式表示?(1)京沪线铁路全程为1463km,乘坐某次列车所用时间t(单位:h)随该列车平均速度v(单位:km/h)的变化而变化;(2)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长为y随宽x的变化;(3)已知北京市的总面积为1.68×104平方千米,人均占有土地面积S(单位:平方千米/人)随全市人口n(单位:人)的变化而变化. 1、上面问题中,自变量与因变量分别是什么?三个问题的函数表达式分别是什么?生:(1)![]() (2)
(2)![]() (3)S=
(3)S=![]() 2、这三个函数关系式可以叫正比例函数吗?可以叫一次函数吗?生: 不可以,也不可以师:这就是我们这节课要探讨学习的新内容:板书:反比例函数。二、新知讲解1、上述问题中的函数关系式都有
2、这三个函数关系式可以叫正比例函数吗?可以叫一次函数吗?生: 不可以,也不可以师:这就是我们这节课要探讨学习的新内容:板书:反比例函数。二、新知讲解1、上述问题中的函数关系式都有![]() 的形式,其中k为常数. 归纳 一般地,形如
的形式,其中k为常数. 归纳 一般地,形如![]() (k为常数,且k≠0)的函数称为反比例函数。(inverseprorportional function) 注意 在
(k为常数,且k≠0)的函数称为反比例函数。(inverseprorportional function) 注意 在![]() 中,自变量x是
中,自变量x是![]() 分式的分母,当x=0时,分式
分式的分母,当x=0时,分式![]() 无意义,所以x的取值范围 x≠0 . 探究 在上面的三个问题中,两个变量的积均是一个常数(或定值),这也是识别的两个量是否成反比例函数关系的关键.注意:三种等价形式:2、巩固练习 例1:下列函数中哪些是反比例函数? (1)
无意义,所以x的取值范围 x≠0 . 探究 在上面的三个问题中,两个变量的积均是一个常数(或定值),这也是识别的两个量是否成反比例函数关系的关键.注意:三种等价形式:2、巩固练习 例1:下列函数中哪些是反比例函数? (1)![]() ;⑵y=2x ⑶
;⑵y=2x ⑶![]() ;(4)
;(4)![]() ;(5)
;(5)![]() ;(6)
;(6) ![]() (7)
(7) ![]() (8)
(8) ![]() (9)
(9)![]() (10)
(10)![]() (11)
(11)![]() (12)
(12)![]() (13)
(13)![]() 生: 反比例函数有:⑶(5) (6) (7) (9) (10) (13)练习:当m= 时,关于x的函数y=(m+1)xm2-2是反比例函数?练习:当m取什么值时,函数
生: 反比例函数有:⑶(5) (6) (7) (9) (10) (13)练习:当m= 时,关于x的函数y=(m+1)xm2-2是反比例函数?练习:当m取什么值时,函数 ![]() 是x的反比例函数? 例2 已知y是x的反比函数,并且当x=2时,y=6.(1)写出y关于x的函数解析式(2)当x=4时,求y的值.解:(1)设
是x的反比例函数? 例2 已知y是x的反比函数,并且当x=2时,y=6.(1)写出y关于x的函数解析式(2)当x=4时,求y的值.解:(1)设![]() ,因为当x=2时,y=6,所以有
,因为当x=2时,y=6,所以有 ![]() 解得K=12因此
解得K=12因此![]() (2)把x=4代入
(2)把x=4代入![]() 得
得![]() 【点拨】(1)由题意,可设y=
【点拨】(1)由题意,可设y=![]() ,把x=2,y=6代入即可求得k,进而求得y关于x的函数关系式.(2)在(1)所求得的函数关系式中,把x=4代入即可求得y的值.练习:变式:y是x+1的反比例函数,当x=3时,y=4 (1)写出y与x的函数关系式.
,把x=2,y=6代入即可求得k,进而求得y关于x的函数关系式.(2)在(1)所求得的函数关系式中,把x=4代入即可求得y的值.练习:变式:y是x+1的反比例函数,当x=3时,y=4 (1)写出y与x的函数关系式.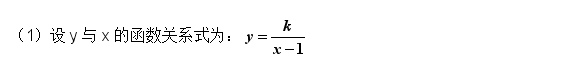 (2)求当y=4时x的值.
(2)求当y=4时x的值.![]() ∵当x=3时,y=-6
∵当x=3时,y=-6![]()
![]() ∴ k=-12
∴ k=-12![]() 三、当堂训练 [中考链接]1.若函数y=(m+1)x|m|-2是反比例函数,则m的值为( B )(A)-1 (B)1 (C)2或-2 (D)-1或12.(桂林·中考)若反比例函数 的图象经过点(-3,2),则k的值为( A )(A)-6 (B)6 (C)-5 (D)53.(威海·中考)下列各点中,在函数
三、当堂训练 [中考链接]1.若函数y=(m+1)x|m|-2是反比例函数,则m的值为( B )(A)-1 (B)1 (C)2或-2 (D)-1或12.(桂林·中考)若反比例函数 的图象经过点(-3,2),则k的值为( A )(A)-6 (B)6 (C)-5 (D)53.(威海·中考)下列各点中,在函数![]() 的图象上的是( C )(A)(-2,-4) (B)(2,3) (C)(-6,1) (D)(- ,3)4.下列关系中是反比例函数的是( C )(A)
的图象上的是( C )(A)(-2,-4) (B)(2,3) (C)(-6,1) (D)(- ,3)4.下列关系中是反比例函数的是( C )(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)y=
(D)y=![]() -15.若点(4,m)在反比例函数
-15.若点(4,m)在反比例函数![]() (x≠0)的图象上,则m的值是___2___.6.已知A(x1,y1),B(x2,y2)都在
(x≠0)的图象上,则m的值是___2___.6.已知A(x1,y1),B(x2,y2)都在![]() 的图象上.若x1x2=-3,则y1y2的值为__-12__四、课堂小结通过本课时的学习,需要我们1.掌握反比例函数的定义,并以此判断是否是反比例函数.2.能根据实际问题中的条件或待定系数法确定反比例函数的解析式.五、布置作业六、板书设计反比例函数一、定义:一般地,形如
的图象上.若x1x2=-3,则y1y2的值为__-12__四、课堂小结通过本课时的学习,需要我们1.掌握反比例函数的定义,并以此判断是否是反比例函数.2.能根据实际问题中的条件或待定系数法确定反比例函数的解析式.五、布置作业六、板书设计反比例函数一、定义:一般地,形如 ![]() ,k≠0 的函数,我们称为反比例函数. 等价形式:
,k≠0 的函数,我们称为反比例函数. 等价形式:![]() xy=k y=kx-1二、例题分析例1、例2、三、练习四、小结
xy=k y=kx-1二、例题分析例1、例2、三、练习四、小结
相关教案
这是一份人教版八年级下册20.1.1平均数教案设计,共8页。教案主要包含了创设情境,引发猜想,验证猜想,探索新知,点击生活,应用新知,回眸课堂,自我提升等内容,欢迎下载使用。
这是一份初中数学人教版七年级下册5.1.1 相交线教案设计,共3页。教案主要包含了学前准备,探索与思考,应用等内容,欢迎下载使用。
这是一份人教版七年级下册8.1 二元一次方程组教案,共5页。教案主要包含了二元一次方程定义等内容,欢迎下载使用。









