数学九年级上册5 一元二次方程的根与系数的关系公开课教案设计

*5 一元二次方程的根与系数的关系

【知识与技能】

掌握一元二次方程根与系数的关系，会运用关系定理求已知一元二次方程的两根之和及两根之积，并会解一些简单的问题.

【过程与方法】

经历一元二次方程根与系数关系的探究过程，培养学生的观察思考、归纳概括能力，解决问题的能力，渗透整体的数学思想、求简思想.

【情感态度】

通过学生自己探究，发现根与系数的关系，增强学习的信心，培养科学探究精神.

【教学重点】

根与系数的关系及运用.

【教学难点】

定理的发现及运用.

一、情境导入,初步认识

我们知道生活中许多事物存在着一定的规律，有人发现并验证后就得到伟大的定理，而我们数学学科中更蕴藏着大量的规律.那么一元二次方程中是否也存在什么规律呢？今天我们共同去探究，感受一次当科学家的滋味.

【教学说明】让学生感受到数学和其他学科一样，里边有很多有价值的规律，等待我们去探索，激发学生的学习兴趣、探究欲望.

二、思考探究，获取新知

解下列方程，将得到的解填入下面的表格中，观察表中x1+x2，x1·x2的值，它们与对应的一元二次方程的各项系数之间有什么关系？从中你能发现什么规律？

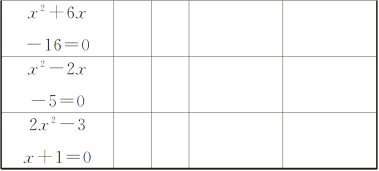
【教学说明】通过学生计算一些特殊的一元二次方程的两根之和与两根之积，引导学生从中发现存在的一般规律，渗透特殊到一般的思考方法.

【归纳总结】一般地，对于关于x的一元二次方程ax2+bx+c=0(a≠0) ，用求根公式求出它的两个根x1、x2 ，由一元二次方程ax2+bx+c=0的求根公式知x1=，x2=，能得出以下结果：

x1+x2=-，x1·x2=.

【教学说明】让学生自己发现规律，找到成功感，再从理论上加以验证，让学生经历从特殊到一般的科学探究过程.

三、运用新知，深化理解

1.求下列方程的两根之和与两根之积.

（1）x2-6x-15=0；

（2）5x-1=4x2；

（3）x2=4；

（4）2x2 =3x.

2.已知关于x的方程x2-2（k-1）x+k2=0有两个实数根x1，x2.

（1）求k的取值范围；

（2）若|x1+x2|=x1x2-1，求k的值.

【教学说明】让学生初步学会运用根与系数的关系来求两根和与两根积.

3.已知方程5x2+kx-6＝0的一个根为2，求它的另一个根及k的值；

解：设方程的另一个根是x1，

那么2x1=

∴ x1=

又x1+2=

∴k=-7

4.利用根与系数的关系，求一元二次方程2x2+3x-1=0的两个根的（1）平方和；（2）倒数和.

解：设方程的两个根分别为x1，x2，

那么x1+x2=，

x1x2=.

（1）∵ （x1+x2）2=x12+2x1·x2+x22，

∴x12+x22=（x1+x2）2-2x1·x2=13/4

（2） = 3

5.已知关于x的方程x2-（k+1）x+1/4k2+1=0，且方程两实根的积为5，求k的值.

解：∵方程两实根的积为5

∴

得 .

∴当k=4时，方程两实根的积为5.

6.已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根.

（1）求实数k的取值范围；

（2）0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由.

解：（1）Δ=［ 2（k-1）］ 2-4（k2-1）

=4k2-8k+4-4k2+4=-8k+8.

∵ 原方程有两个不相等的实数根，

∴-8k+8＞0，解得 k＜1，即实数k的取值范围是 k＜1.

（2）假设0是方程的一个根，则代入得 02+2（k-1）· 0+k2-1 = 0，

解得k=-1或 k=1（舍去）.

即当k=-1时，0就为原方程的一个根.

此时，原方程变为 x2-4x = 0，解得 x1=0，x2=4，所以它的另一个根是4.

【教学说明】目的是考察学生灵活运用知识解决问题的能力，让学生了解到根与系数的关系在解题中的运用，同时也考察学生思维的严密性.

四、师生互动，课堂小结

不解方程，根据一元二次方程根与系数的关系和已知条件结合，可求得一些代数式的值；求得方程的另一根和方程中的待定系数的值：

（1）先化成一般形式，再确定a,b,c. 

（2）当且仅当b2-4ac≥0时，才能应用根与系数的关系.

（3）要注意符号：两个根的和是前面有负号，两个根的积是前面没有负号.

让学生谈谈本节课的收获与体会，教师可适当引导和点拨.

1.布置作业：教材“习题2.8”中第2 、3题.

2.完成练习册中相应练习.

此节课在研究方程的根与系数关系时，先从具体例子观察、归纳其规律，并且先从二次项系数是1的方程入手，然后提出二次项系数不是1的方程，由此，猜想一般的一元二次方程的根与系数的关系，最后对此猜想的正确性作出证明.这个全过程对培养学生正确的思考方法很有价值.