北师大数学九上 第三章 概率的进一步认识复习教案及反思

本章复习

【知识与技能】

回顾本章内容，用所学的概率知识去解决某些现实问题，再归纳和总结试验频率与理论概率的关系.

【过程与方法】

学会与人合作，进一步发展学生合作交流的意识和能力.

【情感态度】

形成解决问题的一些策略，体验解决问题的多样性，发展实践能力和创新精神.

【教学重点】

用所学的概率知识去解决某些现实问题.

【教学难点】

用所学的概率知识去解决某些现实问题.

一、知识结构

【教学说明】通过回顾知识点，使学生掌握各知识点之间的联系.

二、释疑解惑，加深理解

1.用树状图或表格求概率.

回顾：用树状图或表格求概率时应注意什么情况？

2.用频率估计概率.

如何用频率估计概率？

【教学说明】让学生通过知识性内容的小结，了解本章所学内容，如何用所学知识解决实际问题.

三、典例精析，复习新知

1.十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒．当你抬头看信号灯时，是黄灯的概率是（   ）

A.1/3        B.5/12         C.1/12          D.1/2

解析：让黄灯亮的时间处于总时间即为抬头看信号灯时，是黄灯的概率.每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒共60秒，所以是黄灯的概率是5/60=1/12.故选C.

解答：C

2.以下说法合理的是（   ）

 A.小明在10次抛图钉的试验中发现有3次钉尖朝上，由此他说钉尖朝上的概率是30%

 B.抛掷一枚普通的正方体骰子，出现6的概率是1/6的意思是每6次就有1次掷得6

 C.某彩票的中奖机会是2%，那么如果买100张彩票一定有2张中奖

 D.在一次课堂上进行的试验中，甲、乙两组同学估计硬币落地后，正面朝上的概率分别为0.48和0.51

解析：概率是反映事件发生机会的大小的概念，只是表示发生的机会的大小，机会大也不一定发生.A选项，10次抛图钉的试验太少，错误；B选项，概率是反映事件发生机会的大小的概念，机会大也不一定发生，错误；C选项，概率是反映事件发生机会的大小的概念，机会大也不一定发生，错误；D选项，根据概率的统计定义，可知正确.

解答：D

3.如图，图中的两个转盘分别被均匀地分成5个和4个扇形，每个扇形上都标有数字，同时自由转动两个转盘，转盘停止后，指针都落在奇数上的概率是（   ）

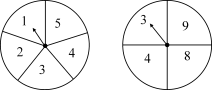
A.2/5         B.3/10         C.3/20        D.1/5

解析：列举出所有情况，看转盘停止后，指针都落在奇数上的情况数占总情况数的多少即可.列表得：

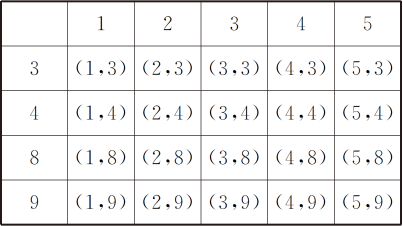
所以两个转盘的组合有20种结果，其中有6种指针都落在奇数，所以指针都落在奇数上的概率是6/20=3/10，故选B.

解答：B

4.小明每天骑自行车上学都要经过三个安装有红绿灯的路口，假如每个路口红灯和绿灯亮的时间相等，那么，小明从家随时出发去学校，他至少遇到一次红灯的概率是多少？不遇红灯的概率是多少？

分析：用列举法列举出符合题意的各种情况的个数，再根据概率公式解答即可.

解：A表示红灯，B表示绿灯，根据题意画出树状图，如图所示：

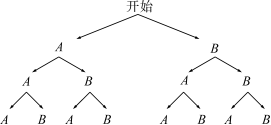
他至少遇到一次红灯的概率是7/8；不遇红灯的概率是1/8.

【教学说明】通过例题的分析和讲解，突出本章内容的重点、难点和解题的方法.在整节课中起到画龙点睛的作用.

四、复习训练，巩固提高

1.某学校的初二（1）班，有男生20人，女生24人，其中男生有18人住宿，女生有20人住宿．现随机抽一名学生，则抽到一名走读女生的概率是_______.

解析：本题考查了概率的简单计算能力，是一道列举法求概率的问题，属于基础题，可以直接应用求概率的公式.共44名学生，其中女生24人，有20人住宿，即4人走读．故抽到一名走读女生的概率是4/44=1/11.

解答：1/11

2.小明与小亮在一起做游戏时需要确定做游戏的先后顺序，他们约定用“锤子、剪刀、布”的方式确定，请问在一个回合中两个人都出“布”的概率是______.

解析：小明与小亮在用“锤子、剪刀、布”的方式确定时共9种结果，故在一个回合中两个人都出“布”的概率是1/9.

解答：1/9

3.中央电视台《幸运52》栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）．某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是________.

解析：本题考查了概率的简单计算能力，是一道列举法求概率的问题，属于基础题，可以直接应用求概率的公式.∵某观众前两次翻牌均获得若干奖金，即现在还有18个商标牌，其中有奖的有3个，∴他第三次翻牌获奖的概率是3/18=1/6.

解答：1/6

4.口袋里有红球4个、绿球5个和黄球若干个，任意摸出一个球是绿色的概率是1/3.

求：（1）口袋里黄球的个数；

（2）任意摸出一个球是红色的概率.

分析：（1）设口袋中有黄球m个，根据概率的求法求任意摸出一个球是绿色的概率，将1/3代入即可求出m的值；（2）口袋里有红球4个，共有15个球任意摸出一个球是红色的概率为4/15.

解：（1）设口袋中有黄球m个，任意摸出一个球是绿色的概率是5/(4+5+m)=1/3，解可得m=6，即有6个黄球；

（2）口袋里有红球4个，共有4+5+6=15个球，故任意摸出一个球是红色的概率为4/15.

5.将分别标有数字1、2、3的三张硬纸片，反面一样，现把三张硬纸片搅均反面朝上．

（1）随机抽取一张，恰好是奇数的概率是多少？

（2）先抽取一张作为十位数（不放回），再抽取一张作为个位数，能组成哪些两位数，将它们全部列出来，并求所组成的两位数中大于20的概率.

分析：根据概率的求法，找准两点：①符合条件的情况数目；②全部情况的总数，二者的比值就是其发生的概率.

解：（1）根据题意分析可得：有分别标有数字1、2、3的三张硬纸片，其中奇数有2个，故随机抽取一张，恰好是奇数的概率为2/3；

（2）共有12、13、21、23、31、32六种情况，大于20的有4个，故其概率为2/3.

6.某校九年级1，2班联合举行毕业晚会，组织者为了使晚会气氛热烈、有趣，策划时计划整场晚会以转盘游戏的方式进行，每个节目开始时，两班各派一人先进行游戏，胜者获得一件奖品，负者表演一个节目．1班的文娱委员利用分别标有数字1，2，3和4，5，6，7的两个转盘（如图）设计了一个游戏方案，两人同时各转动一个转盘一次，将转到的数字相加，和为偶数时，1班代表胜，否则2班代表胜，你认为该方案对双方是否公平？为什么？

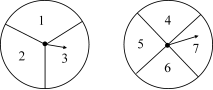
分析：本题考查概率问题中的公平性问题，解决本题的关键是计算出各种情况的概率，然后比较即可：

解：该方案对双方是公平的．理由如下：

列表如下：

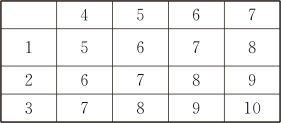
由上表可知，该游戏所有可能的结果共有12种，其中两数字之和为偶数的有6种，和为奇数的也有6种.

所以1班代表获胜的概率为P1=6/12，2班代表获胜的概率为P2=6/12，即P1=P2，所以该游戏方案对双方是公平的.

【教学说明】通过练习，巩固概率的基础知识，加深对概率知识、方法及应用的认识.通过老师的辅导，帮助学生对本节内容进行查漏补缺.

五、师生互动，课堂小结

你有什么收获？请同学们自己谈谈.

【教学说明】师生共同小结.在小结时教师根据学生完成以上练习的情况穿插点评.

布置作业:教材“复习题”中第2、4、5题.

本节课复习课，力求串起全章主要知识点，达到复习目的.使学生具备随机观念，从而能明智地应付变化和不确定性，是概率教学的主要目标.随机观念的培养需要一个长期的过程，教学中以学生自主活动和合作交流为主，使学生在活动中加深对知识的理解，并能进一步应用.