初中数学北师大版九年级上册1 成比例线段完美版课件ppt

第2课时 等比性质

【知识与技能】

1.能用比例的基本性质推出等比性质.

2.学会用设“k”法解答比例的相关题目.

【过程与方法】

经历等比性质的推导过程，掌握并灵活运用等比性质解决相关问题.

【情感态度】

培养学生分析、解决问题的能力，增强数学应用意识，体会数学与现实的紧密联系.

【教学重点】

理解并掌握等比性质.

【教学难点】

等比性质的实际应用.

一、情境导入，初步认识

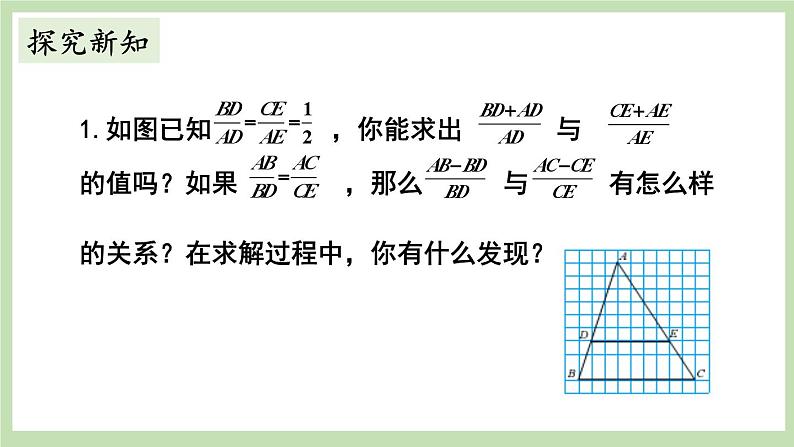
如图，已知，你能求出的值吗？由此你能得出什么结论？

【教学说明】让学生以小组为单位进行思考、探讨和交流，教师采用巡视的方式参与到学生的交流活动中.教师巡视时可关注：①学生的研究方法，发现好的方法时，可在适当时间让其和同学们一起交流分享.②还有哪些小组的同学研究有困难，此时教师可抓住分分秒秒对其进行讲解，争取不让任何一个学生掉队.

二、思考探究，获取新知

已知a，b，c，d，e，f六个数，如果=k，（b=d=f≠0），那么=k成立吗？为什么？

【归纳结论】

如果=k，（b=d=f≠0），那么=k

【教学说明】理解比例的性质可以由等式的基本性质推出.

三、运用新知，深化理解

1.已知（b+d+f≠0），求的值.

分析：根据等比性质，

∵

∴.

2.已知==3，=成立吗？

分析：由==3，得a=3b，c=3d.所以==2， ==2，因此=.

3.已知a∶b∶c=4∶3∶2，且a+3b-3c=14.

（1）求a、b、c；

（2）求4a-3b+c的值.

解：（1）设a=4k，b=3k，c=2k.

∵a+3b-3c=14，

∴4k+9k-6k=14，

∴7k=14，

∴k=2，

∴a=8，b=6，c=4.

（2）4a-3b+c=32-18+4=18.

4.已知a∶b∶c=3∶4∶5，求的值.

解：方法一：由a∶b∶c=3∶4∶5，得，

所以，

所以，所以，

所以.

方法二：由a∶b∶c=3∶4∶5，得，

设=k，

则a=3k，b=4k，c=5k，

所以.

5.在△ABC中，D是BC上一点，若AB=15cm，AC=10cm，且BD∶DC=AB∶AC，BD-DC=2cm，求BC.

解：∵AB=15cm，AC=10cm，

∴.

设BD=3k，DC=2k，

∵BD-DC=2cm，

∴k=2cm.

∴BC=3k+2k=5k=10cm.

【教学说明】让学生清楚的理解比例的基本性质的应用，熟练掌握设“k”法.

6.已知k=，求k的值.

分析：解决这个问题时一定要注意分类讨论，不能只用等比性质，而把a+b+c=0这种情况漏掉.

解：当a+b+c=0时，a+b=-c，k==-1；

当a+b+c≠0时，可以用等比性质k==2；所以k=-1或k=2.

【教学说明】在利用等比性质时，一定要注意等比性质成立的条件，千万不能忽视这一点.

四、师生互动，课堂小结

1.本节课你有哪些收获？

2.通过这节课的学习，你还存在哪些疑惑？

【教学说明】让学生相互交流后，单独回答、提问.

1.布置作业:教材“习题4.2”中第1、2题.

2.完成练习册中相应练习.

本节采用以问题为载体，以培养学生能力为目的的教学模式，教学从提出新的问题开始，引导学生获取知识、探索发现、积极创新，加深对问题的认识，采用讲练结合的方式，增加了教学的弹性.