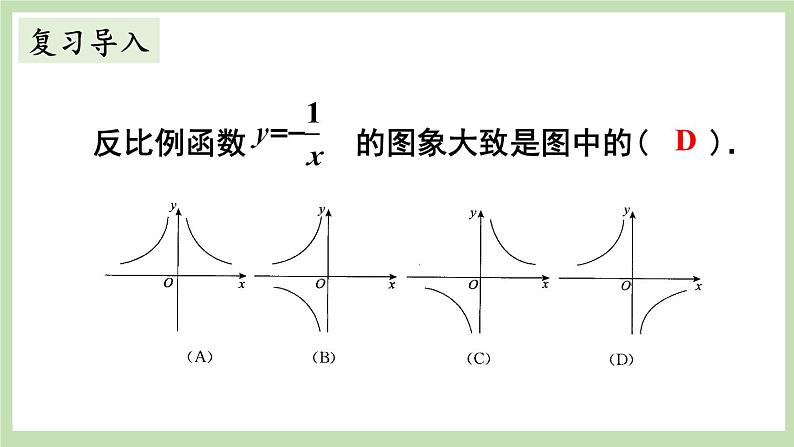
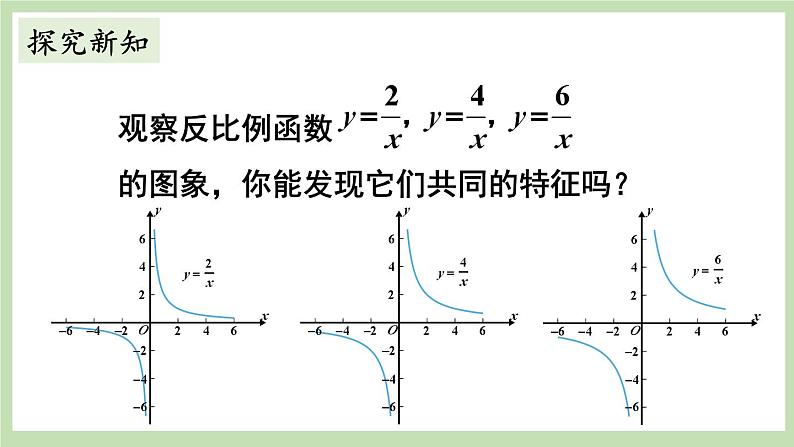
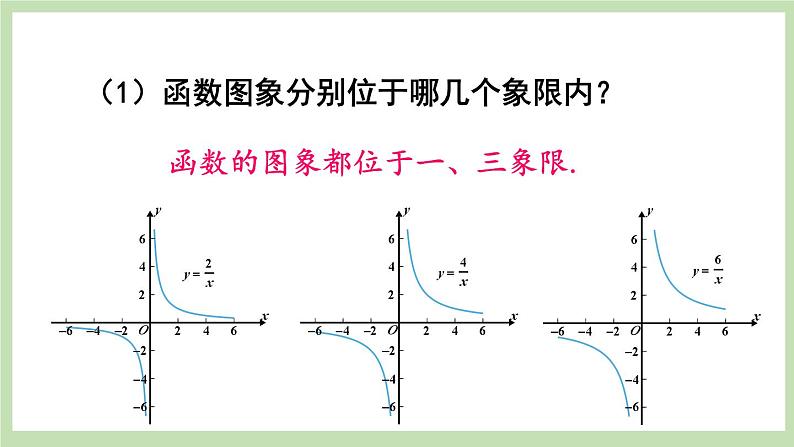
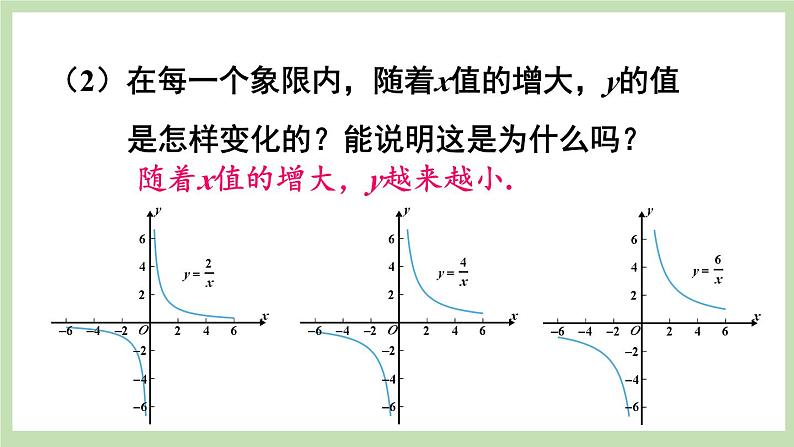
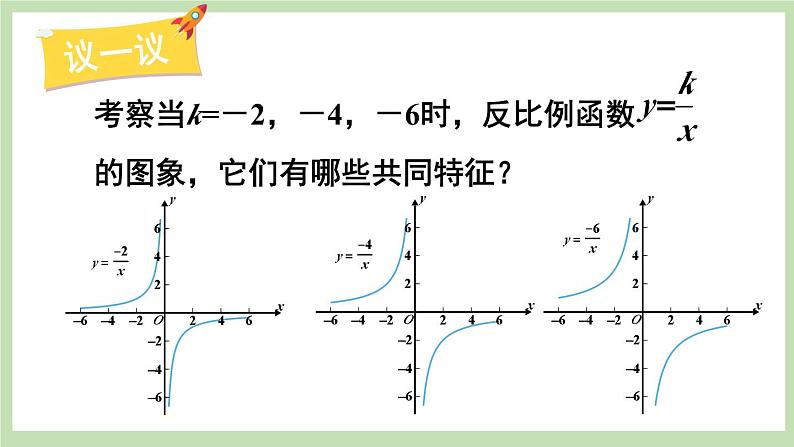
北师大版九年级上册2 反比例函数的图象与性质评优课ppt课件

第2课时 反比例函数的图象与性质（2）

【知识与技能】

探索反比例函数的主要性质.

【过程与方法】

经历观察、归纳、交流的过程，提高学生的观察、分析能力和对图形的感知水平.

【情感态度】

让学生进一步体会用反比例函数刻画现实生活问题的作用．

【教学重点】

准确掌握并能运用反比例函数图象的性质．

【教学难点】

准确掌握并能运用反比例函数图象的性质．

一、情境导入，初步认识

上一节课我们已经学习了反比例函数的定义和图象的画法，及图象所在的象限.今天我们继续来探究反比例函数的图象和它的性质.

【教学说明】通过类比正比例函数的学习，提出本节课所要研究的问题及其研究方法，并引导学生的研究思路．

二、思考探究，获取新知

1.画一画反比例函数y=和y=-的图象.

思考：随着x的增大,y值是怎样变化的？

【教学说明】加深学生对作反比例函数图象的认识，并在列表、画图过程中进一步感知反比例函数的性质.

【归纳结论】反比例函数y=（k≠0）的图象：当k＞0时，在每一象限内，y的值随着x值的增大而减小；当k＜0时，在每一象限内，y的值随着x值的增大而增大.

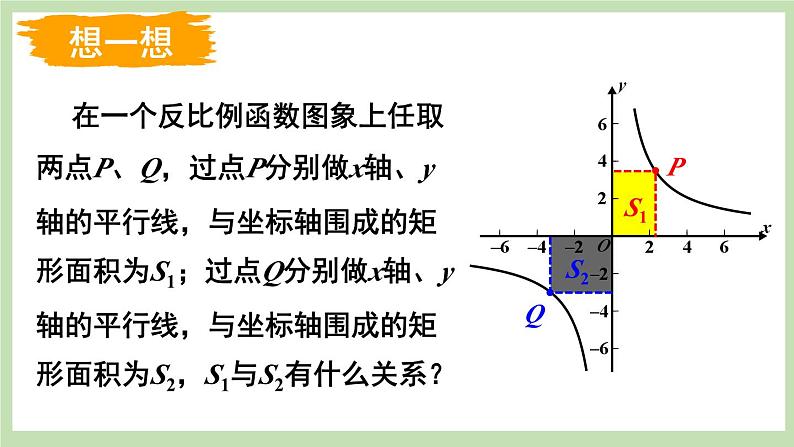
2.在反比例函数y=的图象上取两点Ｐ（1，6），Ｑ（6，1），过点Ｐ分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S1=______；过点Ｑ分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S2=______；S1与S2有什么关系？为什么？

【教学说明】引导学生根据一定的分类标准研究反比例函数的性质，同时鼓励学生用自己的语言进行表述，从而提高学生的表达能力与数学语言的组织能力.

【归纳结论】反比例函数y=（k≠0）中比例系数k的几何意义：过反比例函数y=（k≠0）图象上任意一点引x轴、y轴的平行线，与坐标轴围成的矩形面积为k的绝对值.

三、运用新知，深化理解

1.若点A(7，y1)，B(5，y2)在双曲线y=－上，则y1、y2中较小的是y2．

2.若反比例函数y=，当x＞0时，y随x的增大而增大，则k的取值范围是(A)

A.k＜0            B.k＞0

C.k≤0            D.k≥0

3.下列函数中，当x＞0时，y随x的增大而减小的是(B)

A.y＝x             B.y=

C.y=－           D.y＝

4.反比例函数y＝ ，当x＞0时，y随x的增大而增大，则m的值是(C)

A.±1              B.小于1/2的实数

C.－1              D.1

5.已知点A(x1，y1)，B(x2，y2)是反比例函数y=(k＞0)的图象上的两点，若x1＜0＜x2，则有(A)

A.y1＜0＜y2           B.y2＜0＜y1

C.y1＜y2＜0           D.y2＜y1＜0

6.一次函数y＝kx＋b与反比例函数y=的图象如图所示，则下列说法正确的是(C)

A.它们的函数值y随着x的增大而增大

B.它们的函数值y随着x的增大而减小

C.k＜0

D.它们的自变量x的取值为全体实数

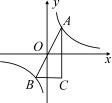
第6题图                 第8题图

7.当k＜0时，反比例函数y=和一次函数y＝kx＋2的图象大致是(B)

8.如图，A、B是函数y=的图象上关于原点对称的任意两点，BC∥x轴，AC∥y轴，△ABC的面积记为S，则(B)

A.S＝2             B.S＝4

C.2＜S＜4          D.S＞4

9.已知点A(m，2)、B(2，n)都在反比例函数y=的图象上．

(1)求m、n的值；

(2)若直线y＝mx－n与x轴交于点C，求C关于y轴对称点C′的坐标.

解：（1）m=n=3； （2）C′（-1，0）.

10.已知正比例函数和反比例函数的图象都经过点A(3，3)．

(1)求正比例函数和反比例函数的解析式；

(2)把直线OA向下平移后与反比例函数的图象交于点B(6，m)，求m的值和这个一次函数的解析式；

(3)在(2)中的一次函数图象与x轴、y轴分别交于C、D，求四边形OABC的面积.

解：(1)y=x,y=；

(2)m=；y=x－;

(3)S四边形OABC＝．

11.如图，反比例函数y=kx的图象与直线y＝x－2交于点A，且A点纵坐标为1，求该反比例函数的解析式.

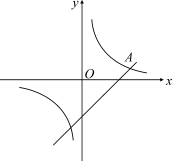
解：将yA=1代入y=x-2

得xA=3，

故A的坐标为（3，1）.

将A(3,1)代入y=得

k=3，

所以反比例函数的解析式为y=.

【教学说明】检测题采取多种形式呈现，增加了灵活性，以基本题为主，也有少量综合问题，可使不同水平的学生均有机会获得成功的体验．

四、师生互动、课堂小结

通过本节课的学习你有哪些收获，还有哪些疑惑？请与同伴交流.

1.布置作业:教材“习题6.3”中第1、2题.

2.完成练习册中相应练习.

本节课是在学生已学完一次函数，并初步认识、感知反比例函数概念之后，对反比例函数的图象和性质的进一步掌握.在教学过程中通过自主探究、小组研讨、学生设计问题等环节充分激发学生的学习兴趣．