初中北师大版4 一次函数的应用完美版ppt课件

这是一份初中北师大版4 一次函数的应用完美版ppt课件，共23页。PPT课件主要包含了你为何选取这几个点，可以有不同取法吗，导入新知，素养目标，探究新知，函数解析式，解析式中未知的系数，满足条件的两定点，一次函数的图象直线，从数到形等内容，欢迎下载使用。

反思 你在作一次函数图象时，分别描了几个点？
引入 在上节课中我们学习了在给定一次函数解析式的前提下，我们可以说出它的图象特征及有关性质；反之，如果给你信息，你能否求出函数的解析式呢？这将是本节课我们要研究的问题.
1.理解待定系数法的意义.
2. 学会运用待定系数法和数形结合思想求一次函数解析式.
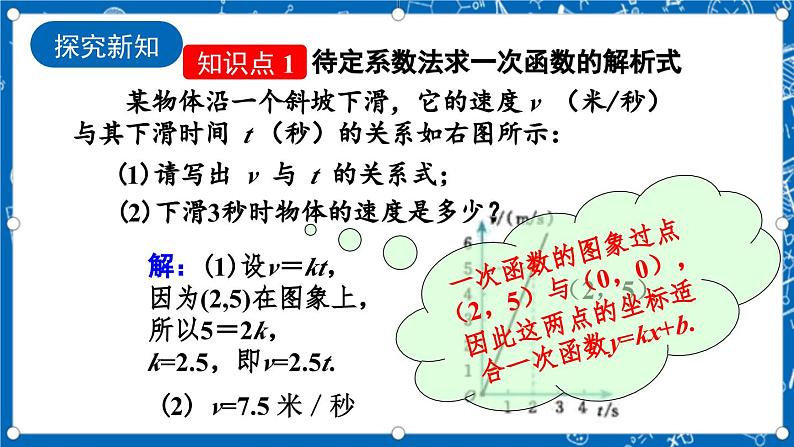
(1)请写出 v 与 t 的关系式；
(2) v=7.5 米／秒
某物体沿一个斜坡下滑，它的速度 v （米/秒）与其下滑时间 t （秒）的关系如右图所示：
解：(1)设v＝kt，因为(2,5)在图象上，所以5＝2k，k=2.5，即v=2.5t.
(2)下滑3秒时物体的速度是多少？
一次函数的图象过点（2，5）与（0，0），因此这两点的坐标适合一次函数y=kx+b.
待定系数法求一次函数的解析式
在弹性限度内，弹簧的长度y（厘米）是所挂物体质量x（千克）的一次函数.一根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米.请写出y与x之间的关系式，并求当所挂物体的质量为4千克时弹簧的长度.
解：设y=kx+b(k≠0) 由题意得：14.5=b,16=3k+b,解得：b=14.5 ; k=0.5.所以在弹性限度内，y=0.5x+14.5,当x=4时，y＝0.5×4+14.5=16.5（厘米）.即物体的质量为4千克时，弹簧长度为16.5厘米.
你能归纳出待定系数法求函数解析式的基本步骤吗？
像这样先设出____________ ，再根据条件确定____________________ ，从而具体写出这个式子的方法，叫做待定系数法.

（1）设：设一次函数的一般形式
求一次函数解析式的步骤:
y=kx+b(k≠0)
（3）解：解几个一次方程得k,b；
（4）还原：把k,b的值代入一次函数的解析式.
函数解析式y=kx+b
整理归纳：从两方面说明：
例1 一次函数图像经过点(2,0)和点(0,6)，写出函数解析式.
这个一次函数的解析式为y=-3x+6.
解：设这个一次函数的解析式为y=kx+b.
把点（2，0）与（0，6）分别代入y=kx+b，得：
已知两点利用待定系数法求一次函数的解析式
已知一次函数的图象过点（3，5）与（0，-4），求这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b.
所以这个一次函数的解析式为
把点（3，5）与（0，-4）分别代入，得：
例2 若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行，求其解析式.
已知一点利用待定系数法求一次函数的解析式
方法点拨：两直线平行，则一次函数中x的系数相等，即k的值不变.
因为一次函数图象与直线y= -x+3平行，所以k= -1.
又因为直线过点（2，0）， 所以0=-1×2+b, 解得b=2,
解：设直线l为y=kx+b,因为l与直线y= -2x平行，所以k= -2.又因为直线过点（0，2）， 所以2=-2×0+b,解得b=2,所以直线l的解析式为y=-2x+2.
已知直线l与直线y=-2x平行，且与y轴交于点(0，2)，求直线l的解析式.
例3 已知一次函数的图象过点（0，2），且与两坐标轴围成的三角形的面积为2，求此一次函数的解析式.
注意：此题有两种情况.
几何面积和待定系数法求一次函数的解析式
解：设一次函数的解析式为y=kx+b(k≠0),因为一次函数y=kx+b的图象过点（0，2），所以b=2，因为一次函数的图象与x轴的交点是( ，0)，则 解得k=1或-1.故此一次函数的解析式为y=x+2或y=-x+2.
正比例函数y=k1x与一次函数y=k2x+b的图象如图所示，它们的交点A的坐标为(3，4)，并且OB=5.(1)你能求出这两个函数的解析式吗？
(2)△AOB的面积是多少呢？
分析：由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3，4)，y=k2x+b的图象过点A(3，4)，B(0,-5)，代入解方程(组)即可.
解：（1）由题意知道，B点的坐标是（0，-5）因为一次函数y=k2x+b的图象过点（0，-5），（3,4）代入得， 因此y=3x-5.因为正比例函数y=k1x的图象过点（3,4），得 ， 因此 ，
S△AOB=5×4÷2=10.
第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢．结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是（　　）A． B． C． D．
3.一次函数的图象如图所示，则k、b的值分别为( )
A.k=-2,b=1 B.k=2,b=1C.k=-2,b=-1 D.k=2,b=-1
4. 如图，直线l是一次函数y=kx+b的图象，填空:　(1)b=______,k=______; (2)当x=30时，y=_____; (3)当y=30时，x=_____.
若一直线与另一直线y=-3x+2交于y轴同一点，且过（2，-6），你能求出这条直线的解析式吗？
分析：直线y=-3x+2与y轴的交点为(0,2)，于是得知该直线过点(0,2)，(2，-6)，再用待定系数法求解即可.
已知一次函数y=kx+b(k≠0)的自变量的取值范围是－ 3≤x≤ 6，相应函数值的范围是－ 5≤y≤ － 2 ，求这个函数的解析式.
分析：(1)当－ 3≤x≤ 6时，－ 5≤y≤ － 2，实质是给出了两组自变量及对应的函数值； (2)由于不知道函数的增减性，此题需分两种情况讨论.
用待定系数法求一次函数的解析式
2. 根据已知条件列出关于k，b的方程；
1. 设所求的一次函数解析式为y=kx+b（k≠0）；
3. 解方程，求出k，b;
4. 把求出的k，b代回解析式即可.