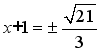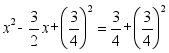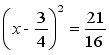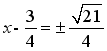数学第二十一章 一元二次方程21.2 解一元二次方程21.2.1 配方法优质课第2课时教学设计

教学

环节

教师活动

学生活动

设计意图

教学目标

【学习目标】

1.理解配方法，会利用配方法熟练地解二次项系数为1的一元二次方程；

2.会利用配方法灵活地解决二次项系数不为1的一元二次方程；

3.通过不同方程的转化，获得解决问题的经验，体会数学中的转化思想；

4. 经历由已知知识到新知识的探究过程，培养学生观察能力和运用所学过的知识解决问题的能力，使学生感受数学的严谨性以及数学结论的确定性.

熟悉学习目标

通过学习目标让学生熟悉本节课要讲解的内容.

环节一

创设情景

【回顾旧知】

教师活动：请同学们跟随老师一起练习上节课内容，着重说明第（4）题的配方

互动方式：全班作答

1.  解方程：

（1）

（2）

（3）

（4）

答：（1）x1=3, x2= – 3

（2）x1=0, x2=4

（3）x1=0, x2= – 6

（4）(y – 3)2=36

y1=9, y2= – 3

2.  填空：

(1)  a2+2ab+b2=__ (a+b)2______

(2)  a2 – 2ab+b2=___ (a – b)2______

(3)  x2 +mx+9是完全平方式，m=__±6_______

(4)  4x2 +12x+a是完全平方式，a=____9_____

教师活动：在问题2中讲解（3）（4）时，着重说明常数项是一次项系数一半的平方，注重演示及方法阐述.

集体回答问题

练习上节课的解方程问题，为后面内容做铺垫.

结合前面学习过的完全平方公式来配方，为后面配方法解方程做方法铺垫.

环节二探究新知

【探究】

问题:怎样解方程x2+6x+4=0 ?

互动方式：分组讨论

教师活动：在分组讨论前，提示学生怎样解方程    x2+6x+9=0?，并演示过程，强调等号左边正好能配成完全平方式，那么x2+6x+4=0与怎样解方程x2+6x+9=0有何区别？分组讨论完后，找学生来阐述思路.再演示过程及解说.

解：x2+6x+4=0

x2+6x= – 4

x2+6x+9= – 4+9

(x+3)2= 5

【归纳】

通过配成完全平方形式来解决一元二次方程的方法，叫做配方法.

跟随老师填空

集体回答问题

通过经历由已知知识到新知识的探究过程，培养学生观察能力和运用所学过的知识解决问题的能力，使学生感受数学的严谨性以及数学结论的确定性.

环节三应用新知

【典例探究】

解下列方程：

(1)   x2 – 8x+1=0

(2)   2x2 +1=3x

(3)   3x2 – 6x+4=0

解：(1)  移项，得

 x2 – 8x = – 1

配方，得

x2 – 8x +42= – 1+42

(x– 4)2=15

由此可得

(2) 解：移项，得

2x2 – 3x = – 1

二项式系数化为1，得

配方，得

由此可得

(3) 解：移项，得

3x2 – 6x = – 4

配方，得

因为(x – 1)2≥0，而＜0，

即原方程无实数根.

【归纳】

一般地，如果一个一元二次方程通过配方转化成

                  (x+n)2=p

的形式，那么就有：

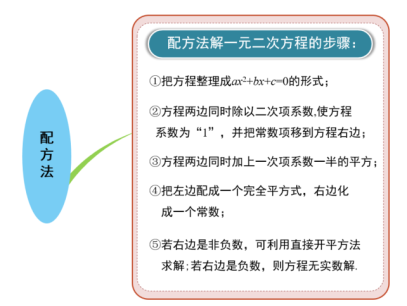
【归纳】

教师活动：根据上一例题的解题过程，逐步誊写配方法解一元二次方程的步骤：

①把方程整理成ax2+bx+c=0的形式；

②方程两边同时除以二次项系数，使方程系数为“1”，并把常数项移到方程右边；

③方程两边同时加上一次项系数一半的平方；

④把左边配成一个完全平方式，右边化成一个常数；

⑤若右边是非负数，可利用直接开平方法求解;若右边是负数，则方程无实数解.

从二次项系数为1到不为1的自然过渡，培养学生用已学的知识解决问题的能力.

环节四

巩固新知

【随堂练习】

练习1

互动方式：抢答

填空：

(1)  x2 + 10x+_____=(x+____)2

(2)  x2 – 12x+_____=(x – ___)2

(3)  x2 + 5x +_____ =(x+____)2

(4)  x2 –    x+_____ =(x – ___)2

答案：（1）25,5（2）36,6（3），（4），

练习2

互动方式：学生独自作答，老师展示书写好的过程.

解下列方程

(1)   x2 +10x+9=0

(2)   x2 – x –=0

(3)   3x2+6x – 4=0

(4)   4x2 – 6x – 3=0

(5)   x2+4x – 9=2x – 11

(6)   x(x+4)=8x +12

答案：

解：（1）x2 +10x+9=0

x2 +10x= – 9

x2 +10x+52= – 9+52

(x+5)2=16

x+5=±4

x1= – 1，x2= – 9

解: (2)

（3）3x2+6x – 4=0

3x2+6x =4

(4) 4x2 – 6x – 3=0

4x2 – 6x =3

(5) x2+4x – 9=2x – 11

x2+2x +2= 0

x2+2x = – 2

x2+2x+12 = – 2+12

(x+1)2 = –1

因为(x+1)2 ≥0，而–1＜0，即方程无实数根.

(6) x(x+4)=8x +12

x2+4x = 8x +12

x2 – 4x = 12

x2 – 4x+22 =12+22

(x– 2)2 = 16

抢答

进一步巩固本节课的内容. 了解学习效果，让学生经历运用知识解决问题的过程，给学生获得成功体验的空间.

通过不同方程的转化，获得解决问题的经验，体会数学中的转化思想.

环节五

课堂小结

以思维导图的形式呈现本节课所讲解的内容.

回顾本节课所讲的内容

通过小结让学生进一步熟悉巩固本节课所学的知识.

环节六

布置作业

教科书

17页习题21.2第2、3题

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.