初中数学人教版九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质精品第2课时教案设计

教学

环节

教师活动

学生活动

设计意图

教学目标

【学习目标】

1. 会用描点法画出二次函数y=a(x-h)² 的图象

2. 通过图象了解二次函数y=a(x-h)²的性质

3. 通过图象了解二次函数y=a(x-h)²与y=ax²图象的关系

4. 掌握二次函数y=a(x-h)²的性质，并会利用性质解决简单问题

熟悉学习目标

通过学习目标让学生熟悉本节课要讲解的内容.

环节一

创设情境

【观察思考】

1.指出下列函数的开口方向、顶点坐标、对称轴

（1）y=-2x²+

（2）y=3x²-

2.抛物线y=x²向上平移3个单位，得到抛物线____

3.抛物线y=-2x²－4向      平移    个单位，得到抛物线y=-2x²+3

答案：2. y=x²+3

      3.上、7

学生通过练习，自主完成练习。

回顾上次课学过的旧知识，引出新知识作铺垫。

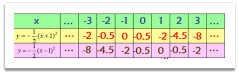
环节二 探究新知

1.画出二次函数、的图象,并考虑它们的开口方向、对称轴和顶点

解：列表、描点

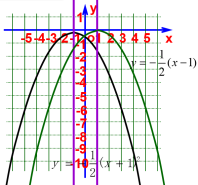
可以看出,抛物线的开口向下

对称轴是经过点(﹣1,0)且与x轴垂直

的直线,我们把它记为x=－1,顶点是(﹣1,0)

抛物线的开口向下，

对称轴是x=1，顶点是（1,0）

学生通过列表、描点、连线。画出二次函数

、

的图象，

培养学生动手操作能力，及观察图象的能力

2.抛物线，与抛物线有什么关系?

学生小组交流，三个二次函数图象的关系，通过数形结合，观察图象具有的性质。

观察图象具有的性质。、两个图象是如何通过平移得到的

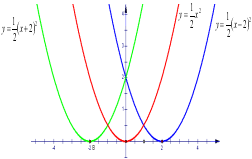
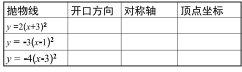
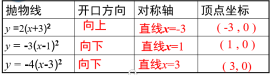
环节三

应用新知

1.在同一坐标系中作出下列二次函数:

、、

观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.

2.二次函数左右平移的口诀

例如：左加右减

学生根据自己总结的规律，画出新的二次函数图象，确定它们的开口方向、对称轴及顶点

教师逐步演示、是如何通过平移得到的，在此过程中，让学生理解平移过程中，对称轴和顶点是如何变化的，理解平移口诀是如何总结出来的。

环节四

巩固新知

答案：

填空：

1.由抛物线y=2x²向左平移_1_个单位可得到y=2(x+1)2

2.函数y= -5(x-4)2的图象。可以由抛物线y=-5x2向右平移4个单位而得到的。它的顶点坐标为 (4,0)

;对称轴为直线x=4

选择题：

 1、若将抛物线y=-2（x-2）²的图象的顶点移到原点，则下列平移方法正确的是（    ）

A、向上平移2个单位

B、向下平移2个单位

C、向左平移2个单位

D、向右平移2个单位

答案：C   .

通过上面的学习，学生自主完成练习题目，小组交流，各自答案，对有疑惑的问题，教师进行解答

对学过的知识进行巩固练习，加深印象。

环节五

课堂小结

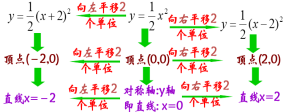
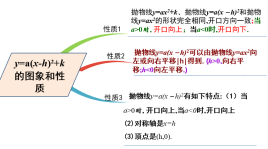
以思维导图的形式呈现本节课所讲解的内容.

回顾本节课所讲的内容

通过小结让学生进一步熟悉巩固本节课所学的知识.

环节六

布置作业

教科书第41页习题22.1

5题（2）

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.