人教版九年级上册22.1.1 二次函数公开课第3课时教案及反思

教学环节

教师活动

学生活动

设计意图

环节一

创设情境

【回顾】

1.二次函数yax2的图象是怎样的呢？有哪些性质？

教师提出问题，全班学生回答，学生回答后，教师PPT呈现结果.

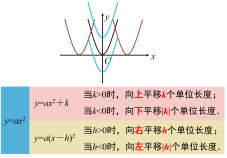
2.怎样由yax2的图象分别得到yax2k、ya(xh)2的图象呢？

教师在上一问题后，继续提问，引导学生回顾，并思考，随机选取学生回答，最后PPT动态展示平移的过程.

根据老师的提问，回顾前面学习的内容，思考并回答.

 通过回顾前面的知识，帮助学生建立起新旧知识之间的联系，为接下来学习新课作铺垫.

环节二 探究新知

【探究】

教师提出问题，可组织学生小组合作，动手操作，得出结论，最后教师汇总补充并呈现结果.

画出函数的图象，并指出它的开口方向、对称轴和顶点.

预设答案：

小组合作，动手操作，并得出结论.

通过画图，培养学生的动手能力，变被动接受为主动探究，激发学生的学习兴趣和求知欲望.加深对二次函数y=a(xh)2k的图象和性质的理解.

【操作】

教师提出问题，学生动手画图，并观察两个函数的图象，思考两者之间的区别和练习，小组交流后选代表回答，教师汇总补充.

1.在同一坐标系中画出的图象；

2.观察这两个函数的图象有什么特点；

3.怎样移动抛物线可得到抛物线.

预设答案：

学生动手画图，观察思考后，小组交流，派代表回答.

通过对比两个函数的图像，建立起知识间的联系.进一步理解二次函数y=a(xh)2k的图象.

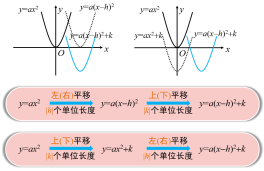
【归纳】

一般地，抛物线ya(xh)2k与yax2形状相同，位置不同，把抛物线yax2向上(下)向左(右)平移，可以得到抛物线ya(xh)2k.平移的方向、距离要根据h、k的值来决定.

抛物线ya(xh)2k有哪些特点呢？

教师提出问题，引导学生从以下几个方面去归纳总结：开口；对称轴与顶点坐标，增减性等等.最终得出结论：

抛物线ya(xh)2k有如下特点：

（1）当a0时，开口向上；当a0时，开口向上；

（2）对称轴是直线xh；

（3）顶点是(h，k).

学生思考，尝试自己先总结.然后小组交流讨论.

归纳梳理二次函数y=a(xh)2k的图象和性质，培养学生的观察能力以及语言组织能力.

【练习】

 1.函数y3x2的图象先向上平移2个单位长度，再向左平移3个单位长度，直接写出平移后的图象表示的二次函数．

答：y3(x3)22

反过来，如果已知y3(x3)22的图象，怎样平移可以得到y3x2的图象？

学生思考并回答.

通过练习，让学生巩固ya(xh)2k的图象和性质，在此基础上进一步锻炼学生逆向思维的能力.

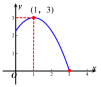
环节三 应用新知

【典型例题】

例1：要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？

追问：还有别的建系方法吗？

教师引导学生发现还有一种比较简单的方法是，让抛物线的最高点在直角坐标系的原点上，但是不管怎样建立直角坐标系，虽然解析式不同，但是最终的结果应该是一致的.

学生观察、思考并回答.

学生小组讨论后，自行解答.

   通过例题讲解，巩固本节课所学知识.

进一步加深对知识的理解，提升综合运用能力.

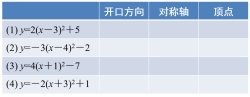
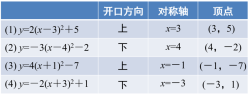
环节四 巩固新知

教师给出练习，随时观察学生完成情况并相应指导，最后给出答案，根据学生完成情况适当分析讲解.

1.指出下列抛物线的开口方向、对称轴和顶点.

答：

2.在平面直角坐标系中，抛物线y=2(x1)26经过怎样的变换可以得到抛物线y2x2 ？

答：方法一：

先向右移1个单位长度，再向上移6个单位长度.

方法二：

先向上移6个单位长度，再向右移1个单位长度.

3.已知函数y2(x1)21，

当x          时， y随x的增大而减小，

当x          时， y随x的增大而增大，

答：1，1

学生自主练习

进一步巩固本节课的内容. 了解学习效果，让学生经历运用知识解决问题的过程，给学生获得成功体验的空间.

环节五 课堂小结

思维导图的形式呈现本节课的主要内容：

通过提问让学生回顾、总结、梳理本节课所学内容.

环节六

布置作业

教科书第41页练习第5、7题.