初中数学人教版九年级上册23.2.2 中心对称图形精品教学设计

教学

环节

教师活动

学生活动

设计意图

教学目标

【学习目标】

1.了解中心对称图形的概念，能够判断一个图形是否为中心对称图形.

2.能够判断出中心对称图形的对称中心，能够区分中心对称图形和中心对称.

3.通过观察、交流等活动，培养学生的概括能力和实践能力.

4.经历观察生活中的中心对称图形，让学生感受现实生活中数学的美，激发学生学习数学的兴趣，培养学生热爱生活的情操.

熟悉学习目标

通过学习目标让学生熟悉本节课要讲解的内容.

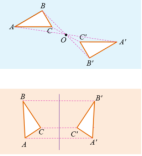
环节一

创设情景

【回顾旧知】

教师活动：引领学生们一起识别中心对称和轴对称（使学生关注是两个图形）；通过复习轴对称图形（使学生关注到是一个图形），创设疑问，中心对称图形是什么呢？.

回答：左图中△ABC与△A′B′C′关于点O对称 (中心对称).

右图中△ABC与△A′B′C′关于直线 l对称 (成轴对称).

学生自由发言

复习轴对称、中心对称、轴对称图形相关知识，通过类比，为下面引进中心对称图形做铺垫.

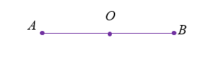
环节二探究新知

【思考】

教师活动：教师依次提出两个问题，动画演示操作，引导学生观察、思考.并引导学生说出它们的共同点.

思考(1) :如图，将线段AB绕它的中点旋转180°，你有什么发现？

回答：将线段AB绕它的中点旋转180°，与它本身重合.

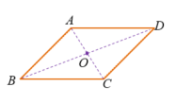
思考(2) : 如图，将□ABCD绕它的两条对角线的交点O旋转180°，你有什么发现？

回答：将□ABCD绕它的两条对角线的交点O旋转180°，与它本身重合.

思考(3) : 能说出这两个图形的共同点吗？

回答：绕着某一个点旋转180°，与原图形重合.

【归纳】

定义：像这样，把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心.

互相重合的点叫做对称点.

教师活动：分析概念要素，帮助学生理解.

线段AB是中心对称图形. 对称中心是点O. A、B为对称点.

平行四边形ABCD是中心对称图形. 对称中心是点O. A、C为对称点；B、D为对称点.

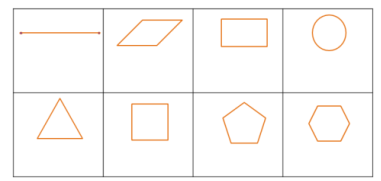
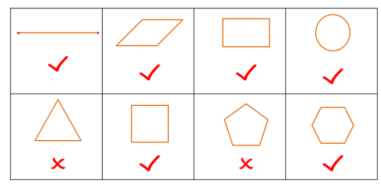
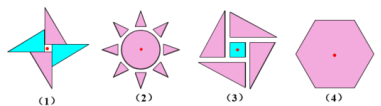
【想一想】

教师活动:引领同学分小组讨论作答，下面8个图形，哪些是中心对称图形，并引导学生观察、思考、归纳、总结正多边形为中心对称图形与边数的关系.

问题：下面8个图形，哪些是中心对称图形?

回答：

追问1：根据表格第二行的图形的情况，观察总结正多边形的边数是多少时，正多边形是中心对称图形？

回答：边数为偶数的正多边形是中心对称图形.

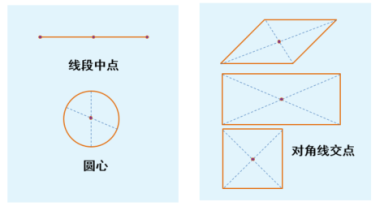
追问2：能找到线段、圆、平行四边形、长方形、正方形的对称中心吗？

教师活动：带领学生们找到对称中心，并总结这些图形对称中心的位置.同时发现中心对称图形的性质并填空.

回答：线段的对称中心为线段的中点；圆的对称中心为圆心；平行四边形、长方形、正方形的对称中心为对角线的交点.

中心对称图形的性质：对称点连线都经过对称中心且被对中心 平分.

【交流】

说说生活中常见到的中心对称图形.

教师活动：智慧课堂操作，让学生发表看法.

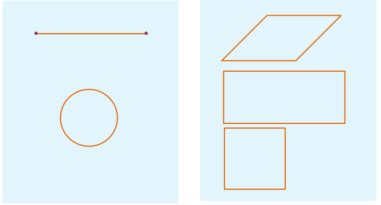
【做一做】

1.  判断下列图形是不是中心对称图形？

答案：不是、是、是.

2.  下列图形是中心对称图形吗？如果是，请指出对称中心.

教师活动：找到对称中心，且教师播放动画，使学生感受事实，且让学生感受中心对称图形顺时针、逆时针旋转180°都重合.

回答：都是中心对称图形.

【归纳】

教师活动：教师带领学生以填空的方式归纳中心对称与中心对称图形的区别与联系；中心对称图形与轴对称图形的区别与联系.

学生进行猜测，并观看教师动画演示

集体回答

分组讨论作答

学生讲

集体回答

通过观察，感受图形变化，从而正确理解中心对称图形的概念.

通过学生自己探讨，进一步加深对中心对称图形的认识.

通过举实例加深印象.

理解概念间的相互关系.

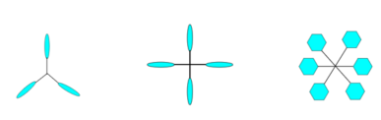
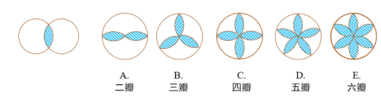
环节三应用新知

【典型例题】

例：将两个大小相等的圆部分重合，其中重叠的部分（如下图的阴影部分）我们称之为一个“花瓣”，由一个“花瓣”及圆组成的图形称之为花瓣图形，下面是一些由“花瓣”和圆组成的图形.

(1) 以上5个图形中是轴对称图形的有_____________，是中心对称图形的有_______；(分别用图形的代号A、B、C、D、E填空).

(2) 若“花瓣”在圆中是均匀分布的，试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律：______________________________________________

回答：

(1)  A、B、C、D、E

A、C、E

(2)  “花瓣”个数为偶数时，这个图形既是轴对称图形又是中心对称图形；“花瓣”个数为奇数时，这个图形是轴对称图形.

小组讨论

.

环节四

巩固新知

【随堂练习】

练习1

判断下列说法是否正确.

（1）轴对称图形也是中心对称图形.（      ）

（2）旋转对称图形也是中心对称图形.（      ）

（3）平行四边形、长方形和正方形都是中心对称图形，对角线的交点是它们的对称中心.（      ）

（4）角是轴对称图形也是中心对称图形.（      ）

（5）在成中心对称的两个图形中，对应线段平行（或在同一直线上）且相等. （      ）

答案：××√×√

练习2

选择题：

下列多边形中，是中心对称图形而不是轴对称图形的是（  ）   

A.   平行四边形

B.   矩形 

C.   菱形 

D.   正方形

答案：A

练习3

下面的扑克牌中，哪些牌面是中心对称图形？

答案：

练习4

在26个英文大写正体字母中，哪些字母是中心对称图形？

A  B  C  D  E  F  G  H  I   J  K  L  M

N  O  P  Q  R  S  T  U  V  W  X  Y  Z

答案:  H  I   N  O  S  X  Z

独立做题

进一步巩固本节课的内容. 了解学习效果，让学生经历运用知识解决问题的过程，给学生获得成功体验的空间.

环节五

课堂小结

以思维导图的形式呈现本节课所讲解的内容.

回顾本节课所讲的内容

通过小结让学生进一步熟悉巩固本节课所学的知识.

环节六

布置作业

巩固例题练习

教科书第69页，习题2.

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.