初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系获奖第2课时教学设计

教学

环节

教师活动

学生活动

设计意图

环节一

创设情境

【学习目标】

1.理解并掌握圆的切线的判定定理和性质定理，并能运用它们解决与圆的切线有关的计算或证明问题；

2.通过探究切线的判定定理和性质定理的过程，领会知识的延续性，进一步培养学生运用已有知识解决数学问题的能力；

3.解决与圆的切线有关的问题时，学会从“数形结合”的角度去思考，学会常用的添加辅助线的方法，学会从反面去思考，发挥逆向思维的作用；

4.经历数学知识的探索和发现过程，体验几何学习中“说理”的无穷乐趣，感受数学思维的严谨性和数学结论的确定性.

熟悉学习目标

通过学习目标让学生熟悉本节课要讲解的内容，教学目标从知识技能、数学思考、解决问题、情感态度等方面着眼设计.

问题：你还记得直线和圆有哪几种位置关系吗？

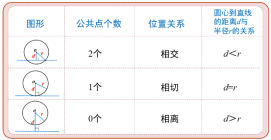
教师带领学生回顾直线和圆的几种位置关系，重点强调本节课要讲解的是直线和圆相切的问题.

问题：我们可以从哪些角度来判断一条直线和圆相切呢？

①       定义法：直线和圆只有一个公共点.

②       数量关系法：圆心到直线的距离等于半径，即d=r.

还有其它的方法能判断直线和圆相切吗？

回顾旧知

总结出直线和圆相切的判断方法

通过回顾旧知帮助学习复习直线和圆的位置关系，同时引出下面的问题：如何判断直线和圆相切.

通过上面复习的知识总结出直线和圆相切的判断方法，领会知识的延续性，进一步培养学生运用已有知识解决数学问题的能力，同时为本节课要学习的切线的判定定理作铺垫.

环节二 探究新知

在⊙O中，经过半径OA的外端点A作直线l⊥OA，则圆心O到直线l的距离是多少，直线l与⊙O有怎样的位置关系呢？

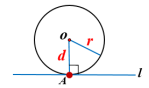
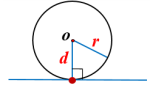
圆心O到直线l的距离=半径r

思考：你能由此得出圆的切线的又一判定方法吗？试着完成下面的表格.

切线的判定定理

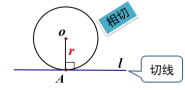
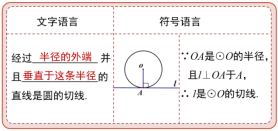
思考：这个定理中包含了哪些要素？

①       经过半径的外端

②       垂直于这条半径

两个条件缺一不可

你能举出生活中直线和圆相切的实例吗？

下雨天快速转动雨伞时飞出的水珠，在砂轮下打磨工件时飞出的火星，都是沿着圆的切线方向飞出的.

思考：已知一个圆⊙O和圆上的一点A，如何过这个点A作出圆的切线？

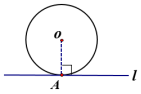
     作法：

    （1）连接OA；

（2）过点A作OA的垂线l，
l即为所作的切线.

圆的切线的判定方法

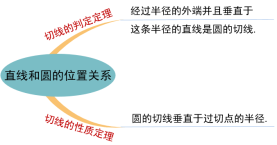
①       定义法：直线和圆只有一个公共点.

②       数量关系法：圆心到直线的距离等于半径，即d=r.

③       判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.

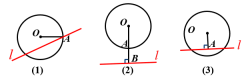
下列各直线是不是圆的切线？如果不是，

请说明为什么？

（1）不是，因为没有与半径垂直

（2）（3）不是，因为没有经过半径的外端点

   思考：如图，在⊙O 中，如果直线 l 是⊙O 的切线，切点为 A，那么半径 OA与直线 l 是不是一定垂直呢？

证明：假设OA与直线l不垂直，

    过点O作一条线段垂直于l，垂足为M，

    由垂线段最短得：OM＜OA，

    即圆心O到直线l的距离小于⊙O的半径，

    因此直线l与⊙O相交，

    这与已知条件“直线l与⊙O相切” 矛盾，

    则OA与直线l垂直．

思考：你能由此得出圆的切线的性质吗？

思考：切线的判定定理和性质定理有什么区别和联系？

联系：交换切线的判定定理的条件和结论，可得到切线的性质定理.

区别：切线的判定定理在未知相切要证明相切时使用；切线的性质定理在已知相切而要得出其它结论时使用.

操作、思考并回答问题

认真完成表格

熟悉切线的判定定理及两个要素

试着举出生活中直线和圆相切的实例

认真思考并作出圆的切线

归纳切线的判定方法

独立完成练习

思考并与同学交流

认真完成表格

通过作图操作让学生感受“直线和圆的位置关系”与“圆心到直线的距离”中的数形结合.

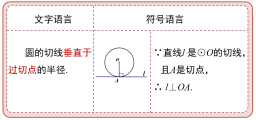
通过表格的形式让学生熟悉切线的判定定理，明确在运用切线的判定定理时两个条件缺一不可，同时要注意文字语言、图形语言和符号语言的相互转化.

通过让学生列举出生活中的实例，进一步熟悉直线和圆相切的情形，同时让学生感受数学来源于生活.

通过“过圆上一点作圆的切线”让学生进一步熟悉切线的判定定理，同时培养学生对于知识的运用能力.

通过归纳总结让学生进一步熟悉切线的几种判定方法，同时培养学生的归纳总结能力.

通过练习进一步让学生熟知：运用切线的判定定理时两个要素缺一不可，同时培养学生独立完成练习的能力.

通过交换切线的判定定理的条件和结论引出新的思考探究，为后面切线的性质定理作铺垫，同时解决这个问题需要用到反证法，从中培养学生的逆向思维能力.

通过表格的形式让学生熟悉切线的性质定理，同时要注意文字语言、图形语言和符号语言的相互转化.

让学生明确切线的判定定理和性质定理之间的联系和区别.感受数学的严谨性.

环节三

应用新知

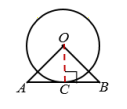
【例1】如图，△ABC 为等腰三角形，O是底边BC的中点，腰AB与⊙O 相切于点D.求证：AC 是⊙O 的切线．

分组讨论：

1.教师带领学生分析解题思路；

2.学生分组进行讨论、整理证明过程；

3.学生展示，教师补充完善.

分析：不知直线和圆的公共点，则过圆心作AC的垂线，证明圆心到直线的距离等于半径即可.

证明：如图，过点O作OE⊥AC，垂足为E，

连接OD，OA.

∵⊙O与AB相切于点D，

∴OD⊥AB.

又△ABC为等腰三角形，O是底边BC的中点，

∴AO是∠BAC的平分线.

∴OE=OD，即OE是⊙O的半径.

这样AC经过半径OE的外端E，并且垂直于半径OE，所以AC与⊙O相切.

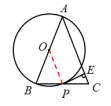
【例2】已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.

自主交流：

1.教师带领学生分析解题思路；

2.学生先独立完成证明过程，再与同桌讨论；

3.学生展示，教师补充完善.

分析：已知直线和圆的公共点C，则连接圆心和公共点，证明直线AB和过公共点的半径OC垂直即可.

证明：连接OC.

      ∵ OA＝OB，CA＝CB,  

      ∴ OC是等腰△OAB底边AB上的中线.　

      ∴ AB⊥OC.

      ∵ OC是⊙O的半径，

      ∴ AB是⊙O的切线.

证切线时常见的添加辅助线的方法

①     不知公共点，作垂直，证半径；

②     已知公共点，连半径，证垂直.

明确本题的做法

明确本题的做法

通过分组讨论的形式帮助学生解决直线和圆相切的问题，让学生明白：当不知直线和圆的公共点时，则过圆心作直线的垂线，证明距离等于半径即可，即“不知公共点，作垂直，证半径”.同时培养学生合作探究的能力.

通过自主的形式帮助学生解决直线和圆相切的问题，让学生明白：当已知直线和圆有公共点时，则可添加过该点的半径，证明直线垂直于该半径即可，即“已知公共点，连半径，证垂直”.同时培养学生独立解决问题的能力.

 通过例题归纳总结出证切线时常见的添加辅助线的方法，培养学生的归纳总结能力.

环节四

巩固新知

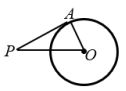
1.判断下列命题是否正确.

 (1)经过半径外端的直线是圆的切线.(    )

 (2)垂直于半径的直线是圆的切线. (    )    

 (3)过直径的外端并且垂直于这条直径的直线是圆的切线. (        )

 (4)和圆只有一个公共点的直线是圆的切线. (  )

 (5)过直径一端点且垂直于直径的直线是圆的切线. （       ）

2.如图所示，A是☉O上一点，且AO=5，PO=13，AP=12，则PA与☉O的位置关系是                 .

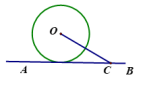
3. 如图，已知⊙O的半径为3，直线AB是⊙O的切线，OC交AB于点C，且∠OCA=30°，则OC的长为_________ .

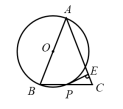
4．如图，△ABC中，AB=AC，以AB为直径的⊙O交边BC于P，PE⊥AC于E.

求证:PE是⊙O的切线.

答案： 1. （1）×；  （2）×；  （3）√

（4）√；  （5）√

2.相切

3.6

4. 证明：连接OP.

    ∵AB=AC,∴∠B=∠C.    

    ∵OB=OP，∴∠B=∠OPB，  

    ∴∠OPB=∠C.  

    ∴OP∥AC.  

    ∵PE⊥AC，

    ∴PE⊥OP. 

    ∴PE为⊙O的切线.

自主完成练习，然后集体交流评价.

通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养独立完成练习的习惯.

环节五

课堂小结

回顾本节课所讲的内容

通过小结总结回顾本节课学习内容，帮助学生归纳、巩固所学知识.

环节六

布置作业

教科书第98页

练习第1、2题

第101页

习题24.2 第5题

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.