24.3《正多边形和圆+第1课时》课件+教案--人教版数学九上

这是一份24.3《正多边形和圆+第1课时》课件+教案--人教版数学九上，文件包含243《正多边形和圆+第1课时》课件--人教版数学九上pptx、243《正多边形和圆+第1课时》教案--人教版数学九上docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

24.3 正多边形和圆第1课时
人教版数学九年级上册
目录
创设情境
探究新知
巩固新知
课堂小结
应用新知
布置作业
1.了解正多边形和圆的关系，了解正多边形的半径、边长、中心、中心角、边心距等概念；2.结合生活中的正多边形形状的图案，发现正多边形和圆的关系，学会用圆的有关知识解决正多边形的问题；3.在探索正多边形和圆的关系的过程中，感受特殊到一般的学习方法，发展学生的逻辑思维能力和推理能力； 4.学生经历观察、发现、探究等数学活动，感受数学来源于生活，又服务于生活，体会事物之间是相互联系、相互作用的.
学习目标
观察思考
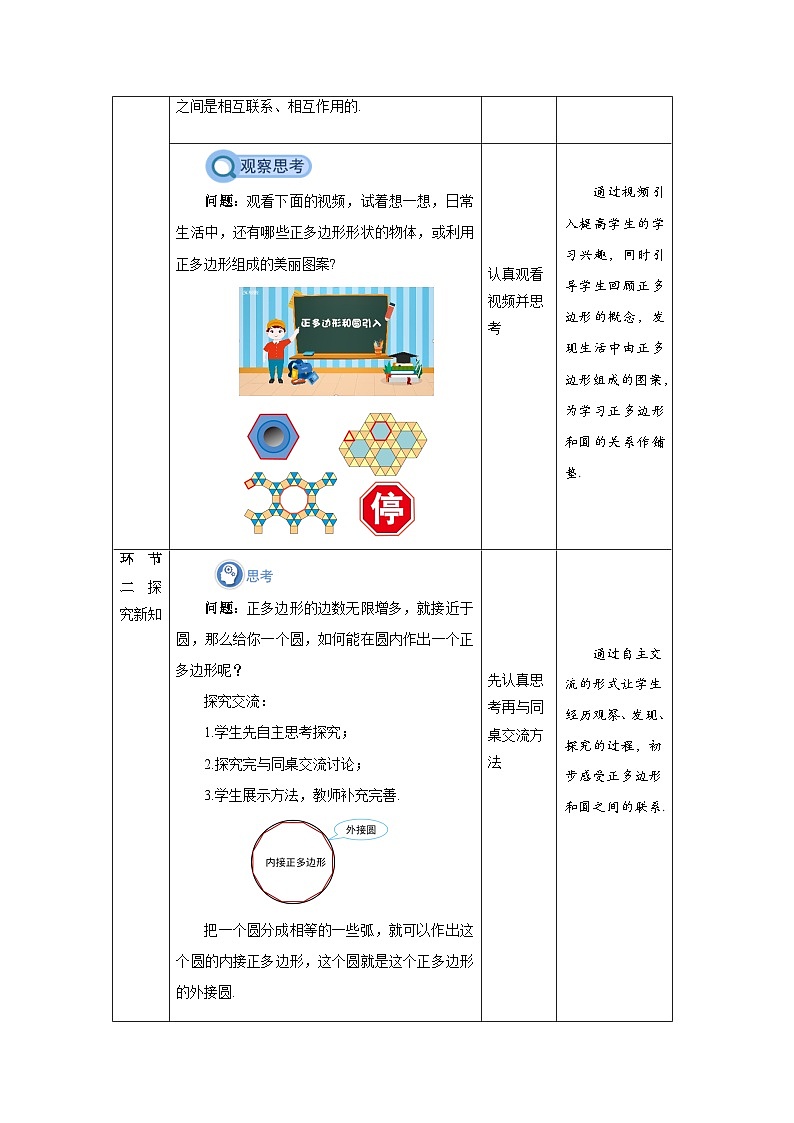
观看下面的视频，试着想一想，日常生活中，还有哪些正多边形形状的物体，或利用正多边形组成的美丽图案?
创设情境
观看下面的视频，试着想一想，日常生活中，还有哪些正多边形形状的物体，或利用正多边形组成的美丽图案?
观察思考
创设情境
正多边形的边数无限增多，就接近于圆，那么给你一个圆，如何能在圆内作出一个正多边形呢？
探究交流：1.学生先自主思考探究；2.探究完与同桌交流讨论；3.学生展示方法，教师补充完善.
探究新知
正多边形的边数无限增多，就接近于圆，那么给你一个圆，如何能在圆内作出一个正多边形呢？
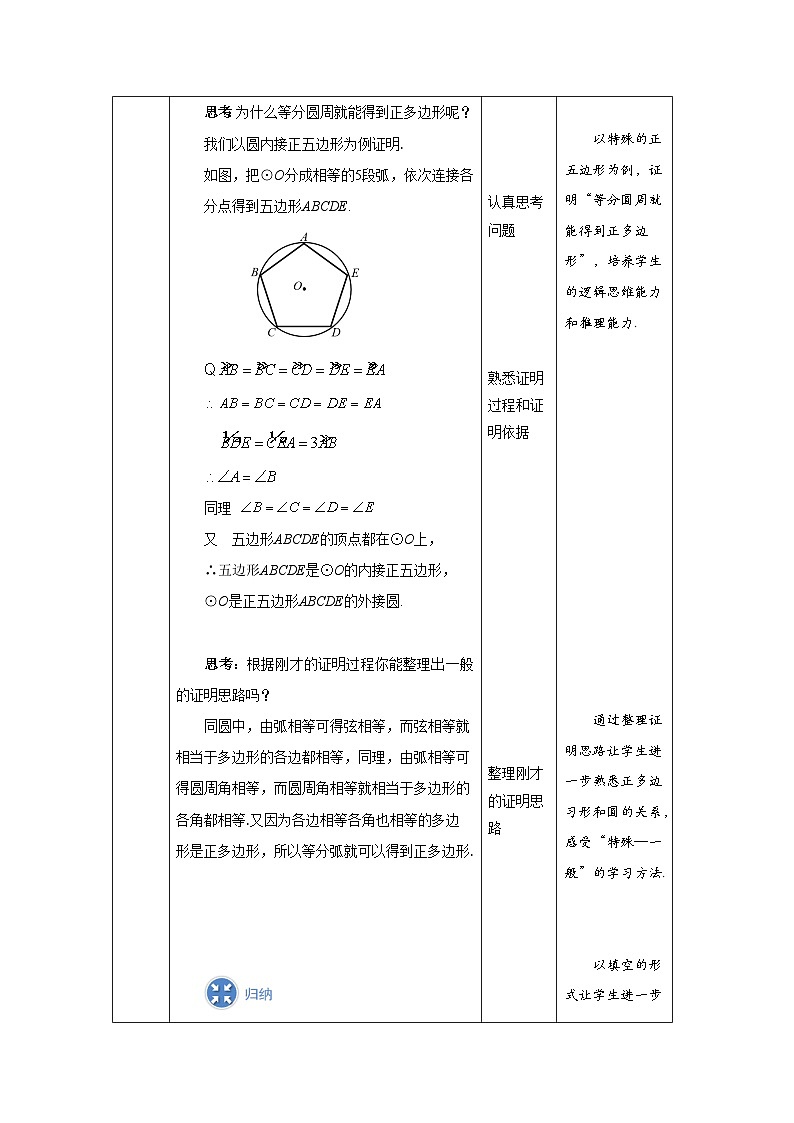
把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆.
外接圆
内接正多边形
探究新知
为什么等分圆周就能得到正多边形呢？
我们以圆内接正五边形为例证明.
如图，把⊙O分成相等的5段弧，依次连接各分点得到五边形ABCDE.
又 五边形ABCDE的顶点都在⊙O上，
∴五边形ABCDE是⊙O的内接正五边形，⊙O是正五边形ABCDE的外接圆.
探究新知
各边相等
各角也相等
正多边形的特征
弧相等
弦相等
圆周角相等
根据刚才的过程你能整理出一般的证明思路吗？
探究新知
把圆分成n（n≥3）等份：依次连接各分点所得的多边形一定是 ，这个正n边形是这个圆的 ，这个圆是这个正n边形的 .
正n边形
内接正n边形
外接圆
探究新知
圆中的元素和正多边形有什么关系呢？
O
中心角
半径R
边心距r
.
A
B
正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
正多边形的每一边所对的圆心角叫做正多边形的中心角.
中心到正多边形的一边的距离叫做正多边形的边心距.
探究新知
完成下面的表格.
正多边形的边数
内角
外角
中心角
3
4
6
n
60°
120°
120°
90°
90°
90°
120°
60°
60°
正多边形的外角=中心角
探究新知
【例】如图，有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积.（结果保留小数点后一位）.
提示：关键是求出正多边形的边长和边心距，作辅助线利用勾股定理求解.
O
B
C
.
应用新知
O
B
C
R
.
因此，亭子地基的周长l =4×6=24(m)．
60°
【例】如图，有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积.（结果保留小数点后一位）.
应用新知
O
B
C
r
P
.
作OP⊥BC，垂足为P，在Rt△OPC中，OC =4， PC =
利用勾股定理，可得边心距
亭子地基的面积
【例】如图，有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积.（结果保留小数点后一位）.
R
应用新知
O
B
C
r
R
P
.
圆内接正多边形常用辅助线
连半径，得中心角
1
2
作边心距，得直角三角形
由勾股定理得
应用新知
1．下列命题正确的是(　 　)　　A．各边相等的多边形是正多边形 　　B．各角相等的多边形是正多边形　　C．既是轴对称图形又是中心对称图形的多边形是正多边形　　D．各边相等，各角也相等的多边形是正多边形
2. 如图，正三角形ABC的外接圆的半径为R，则边长为_____，边心距为______，面积为________．
D
巩固新知
3. 要用圆形铁片截出边长为4 cm的正方形铁片，则选用的圆形铁片的直径最小要 cm.
4. 已知一个正六边形的边心距为 cm，则这个正六边形的周长为 cm.
12
5.在同一个圆中，圆的内接正三角形、正方形、正六边形的边长之比为 .
巩固新知
正多边形和圆
正多边形和圆的关系
正多边形的有关概念
把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆.
正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
正多边形的每一边所对的圆心角叫做正多边形的中心角.
中心到正多边形的一边的距离叫做正多边形的边心距.
课堂小结
教科书第106页练习第1、2、3题第108页习题24.3第1、6题
布置作业
课程结束
人教版数学九年级上册