初中数学人教版九年级上册24.4 弧长及扇形的面积优秀ppt课件

教学

环节

教师活动

学生活动

设计意图

环节一

创设情境

【观察思考】

问题：观察下面的物体，你能抽象出什么相同的几何图形？

圆锥

【思考】

问题：你还能举出一些生活中的圆锥形物体吗？

认真观察

说出常见的圆锥形物体

通过熟悉的生活中实物图片引入，提高学生的学习兴趣，并让学生感受数学与实际生活的联系.

通过举例让学生进一步熟悉圆锥.

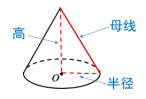
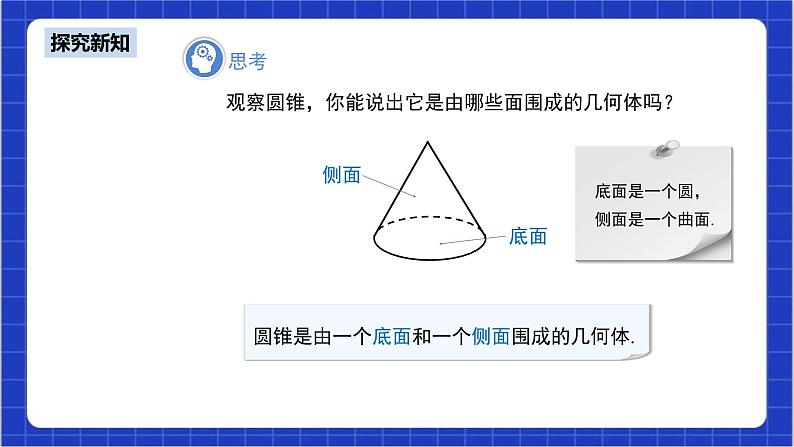
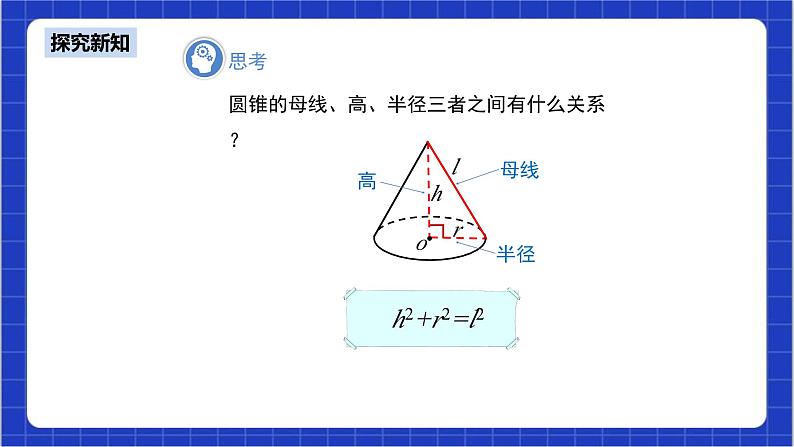
环节二 探究新知

【思考】

教师活动：教师带领学生熟悉圆锥的结构和圆锥中的元素.

问题1：观察圆锥，你能说出它是由哪些面围成的几何体吗？

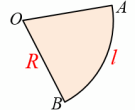
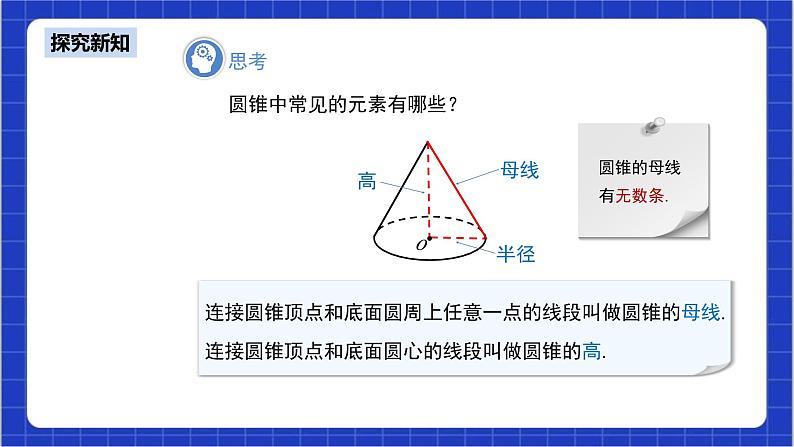
    圆锥是由一个底面和一个侧面围成的几何体. 底面是一个圆，侧面是一个曲面.

追问1：圆锥中常见的元素有哪些？

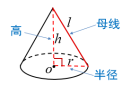
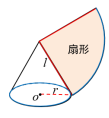
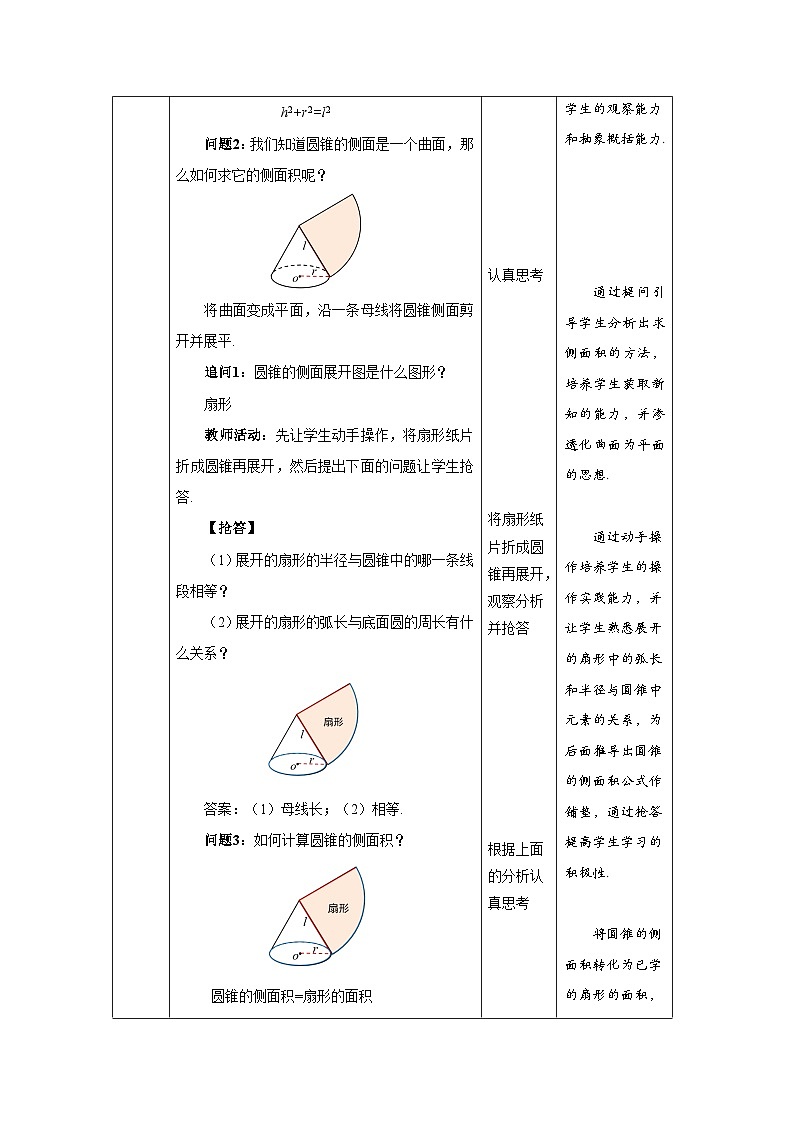
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.圆锥的母线有无数条.

连接圆锥顶点和底面圆心的线段叫做圆锥的高.

追问2：圆锥的母线、高、半径三者之间有什么关系？

h2+r2=l2

问题2：我们知道圆锥的侧面是一个曲面，那么如何求它的侧面积呢？

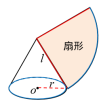
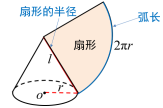
将曲面变成平面，沿一条母线将圆锥侧面剪开并展平.

追问1：圆锥的侧面展开图是什么图形？

扇形

教师活动：先让学生动手操作，将扇形纸片折成圆锥再展开，然后提出下面的问题让学生抢答.

【抢答】

（1）展开的扇形的半径与圆锥中的哪一条线段相等？

（2）展开的扇形的弧长与底面圆的周长有什么关系？

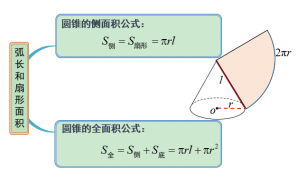
答案：（1）母线长；（2）相等.

问题3：如何计算圆锥的侧面积？

     圆锥的侧面积=扇形的面积

【回顾】扇形的面积公式

S扇形=

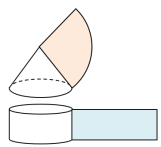
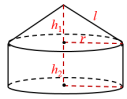
圆锥的侧面积=扇形的面积==

问题4：如何计算圆锥的全面积呢？

圆锥的全面积=侧面积+底面积

            =+

说明：r是底面圆的半径，l是圆锥的母线长.

教师活动：教师提出下面的问题，先让学生自主分析，再播放课件进行动态演示.

问题5：还记得前面提到的蒙古包吗？能否利用今天学到的知识求出蒙古包的全面积？

蒙古包的全面积=圆锥的侧面积+圆柱的侧面积

认真思考

熟悉圆锥中相关元素

熟悉母线、高、半径三者之间的关系

认真思考

将扇形纸片折成圆锥再展开，观察分析并抢答

根据上面的分析认真思考

回顾扇形面积公式

先自主探究、再小组交流

分析出求解思路

通过观察让学生熟悉圆锥的结构和相关元素，培养学生的观察、分析能力.

通过分析得出圆锥的母线、高、半径三者之间的关系，为后面解题作准备，同时进一步培养学生的观察能力和抽象概括能力.

通过提问引导学生分析出求侧面积的方法，培养学生获取新知的能力，并渗透化曲面为平面的思想.

通过动手操作培养学生的操作实践能力，并让学生熟悉展开的扇形中的弧长和半径与圆锥中元素的关系，为后面推导出圆锥的侧面积公式作铺垫，通过抢答提高学生学习的积极性.

将圆锥的侧面积转化为已学的扇形的面积，让学生掌握解决问题的策略.

通过自主探究交流的方式引导学生推导出圆锥的侧面积公式和全面积公式，培养学生分析问题和解决问题的能力.

让学生自主分析出求解思路，学会运用数学知识解决实际问题，进一步感受数学与实际生活的联系，并为后面的例题解答作准备.

环节三

应用新知

【典型例题】

【例】蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12 m2，高为3.2 m，外围高1.8 m的蒙古包，至少需要多少平方米的毛毡（π取3.142，结果取整数）？

探究交流：

1.学生先自主完成例题，再与同桌交流；

2.学生讲述分析解答过程；

3.教师补充完善过程.

解：如图是一个蒙古包的示意图.

根据题意，下部圆柱的底面积为12 m2，高h2=1.8 m；上部圆锥的高h1=3.21.8=1.4（m）.

圆柱的底面圆的半径

r= （m），

侧面积为（m2）.

圆锥的母线长

l=（m），

侧面展开扇形的弧长为                                      

（m），

圆锥的侧面积为     

（m2）.

因此，搭建20个这样的蒙古包至少需要毛毡（m2）.

先自主探究，再与同桌交流

让学生在探究过程中进一步加深对圆锥侧面积公式的理解，培养学生的应用意识.

环节四

巩固新知

【随堂练习】

1.已知一个圆锥的底面半径为12 cm，母线长为20 cm，则这个圆锥的侧面积为_______，全面积为__________.

2.一个圆锥形的冰淇淋纸筒，其底面直径为6 cm，高为4 cm围成这样的冰淇淋纸筒所需纸片的面积为             .

3.若圆锥的底面半径r =4 cm，高线h =3 cm，则它的侧面展开图中扇形的圆心角是     度.

4.童心玩具厂欲生产一种圣诞老人的帽子，其圆锥形帽身的母线长为15 cm，底面半径为5 cm，生产这种帽身10000个，你能帮玩具厂算一算至少需多少平方米的材料吗（不计接缝用料和余料，π取3.14）？

答案：

1.240π cm2；384π cm2；

2.15π cm2；

3.288；

4.解：根据题意，圆锥形帽身的母线长为15 cm，底面半径为5 cm，则其侧面积为

       π515=235.5（cm2）

 因此，生产这种帽身10000个至少需材料 

       235.510000=2355000（cm2）.

自主完成练习，然后集体交流评价.

通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养独立完成练习的习惯.

环节五

课堂小结

回顾本节课所讲的内容

通过小结总结回顾本节课学习内容，帮助学生归纳、巩固所学知识.

环节六

布置作业

教科书第114页

练习第1、2题

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.