


初中数学人教版九年级上册25.2 用列举法求概率获奖ppt课件
展开
第二十五章 概率初步
15.3用列举法求概率
第1课时
一、 教学目标
1.会用直接列举法和列表法求简单事件的概率;
2.能利用概率知识解决涉及两个因素的事件的概率问题;
3.经历试验、列表、统计、运算等活动,渗透数形结合,分类讨论、特殊到一般的思想,培养学生在具体情境中分析问题和解决问题的能力;
4.通过数学活动,体会数学的应用价值,培养积极思考的学习习惯.
二、 教学重难点
重点:会用直接列举法和列表法求简单事件的概率.
难点:当可能出现的结果很多时,会用列表法列出所有可能得结果.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 | 教师活动 | 学生活动 | 设计意图 |
环节一 创设情景 | 【回顾】 教师活动:教师以填空的形式,带领学生回顾简单随机事件求概率的相关内容,接着引入熟悉简单的硬币问题,从而直奔主题,点出列举法.
问题1:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都_相等_,事件A包含其中的m种结果,那么事件A发生的概率P(A) =_ 问题2:掷一枚硬币,正面向上的概率是_ 分析:掷一枚硬币,可能出现的结果有2种: 正面朝上,反面朝上. 这两个结果出现的可能性是相同的.把各种情况列出来,这就是列举法. |
回顾并配合老师回答问题
| 回顾前面学过的求概率的方法,为下面加强列举法打下基础.
|
环节二探究新知 | 【归纳】 在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
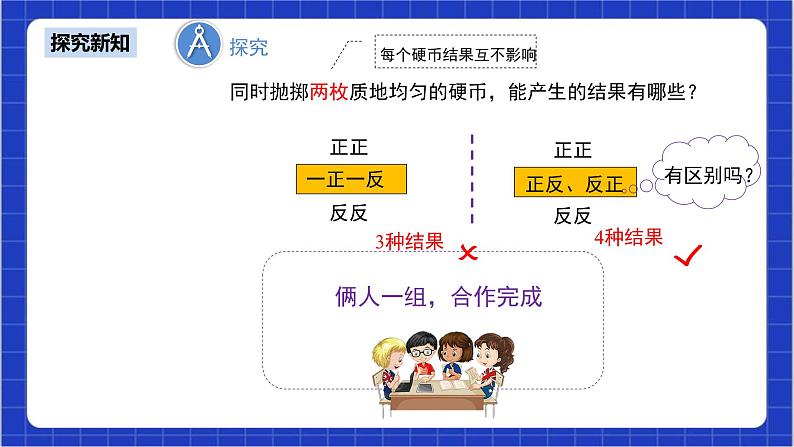
【探究】 教师活动:教师提出问题,引导学生以小组讨论的形式,得出答案,并归纳学生们的结论,预设结论主要为两种形式:正正、一正一反、反反;正正、正反、反正、反反.并引导学生找出这两种结果的区别,判断哪种结果是正确的. 同时抛掷两枚质地均匀的硬币,能产生的结果有哪些? 预设争论答案: 正正、一正一反、反反;(3种结果) 正正、正反、反正、反反.(4种结果)此结果正确.
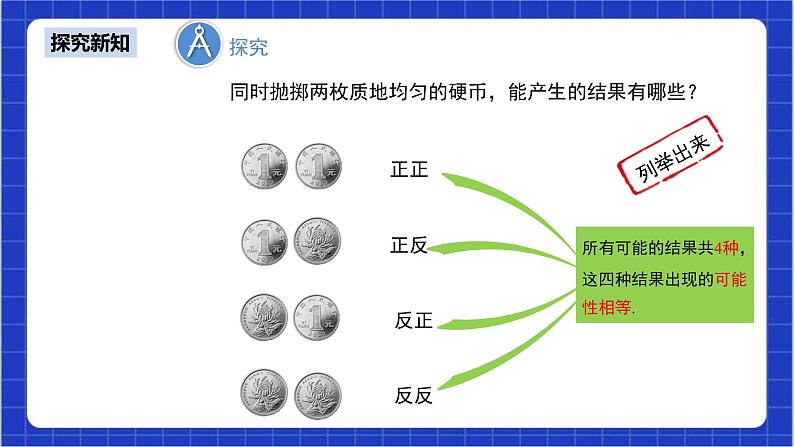
即所有可能的结果共4种,这四种结果出现的可能性相等. 列举出来分别为:正正、正反、反正、反反.
教师活动:以上面问题为背景,接着讨论3个问题,并鼓励学生用列举法,列举出来,加深对列举法的理解.
同时抛掷两枚质地均匀的硬币,求下列事件的概率: (1)两枚硬币全部正面向上; (2)两枚硬币全部反面向上; (3)一枚硬币正面向上;一枚硬币反面向上. 解:列举投掷两枚硬币所能产生的全部结果,它们是: 正正、正反、反正、反反 . 所有可能的结果有 4 个,并且这些结果出现的可能性 相等. ①满足两枚硬币全部正面向上(记为事件A) 的结果只有1种,即“正正”,所以P(A)= ②满足两枚硬币全部反面向上(记为事件B) 的结果只有1种,即“反反”, 所以P(B)= ③满足一枚硬币正面向上;一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反” ,所以P(C)=
教师活动:教师接着上面的问题,追问“先后两次抛掷一枚质地均匀的硬币,能产生的结果有哪些?”以小组讨论的形式展开,让学生加深体会不同事件产生的结果,区分两种事件的同时,体会两个事件产生所有可能的结果是相同的.
先后两次抛掷一枚质地均匀的硬币,能产生的结果有哪些? 与同时抛掷两枚质地均匀的硬币产生的结果一样吗? 答案:一样.
|
小组讨论
小组讨论
|
培养学生在具体情境中分析问题和解决问题的能力.
|
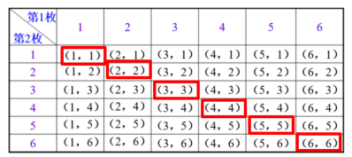
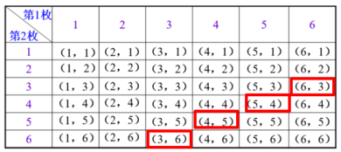
环节三应用新知 | 【典型例题】 教师活动:让学生以小组讨论的形式写出所有可能产生的结果,由于事件较复杂,有两个因素(两个骰子),结果较多,学生会感受到难度,教师因此给出另一种合适的方法——列表法.老师逐步按照分步的方式,把事件分为两步,第1步:掷第1枚骰子,第2步:掷第2枚骰子,然后逐步列表. 例:同时掷两枚质地均匀的骰子,计算下列事件的概率: (2)两枚骰子点数的和是 9; (3)至少有一枚骰子的点数为 2. 当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法. 答案: 解:两枚骰子分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能的结果.用(第1枚点数,第2枚点数)的形式表示结果.
可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相等. (1)
两枚骰子点数相同(记为事件 A)的结果有 6种,即(1,1), (2,2),(3,3),(4,4),(5,5),(6,6). 所以 (2)
两枚骰子点数的和是 9 (记为事件 B)的结果有 4种,即 (3,6),(4,5),(5,4),(6,3). 所以 (3)
至少有一枚骰子的点数为2 (记为事件 C)的结果有 11种,即 (1,2),(2,2),(3,2),(4,2),(5,2),(6,2), (2,1), (2,3),(2,4), ( 2,5),(2,6). 所以
【归纳】 1.用列举法(列表法)求简单随机事件的概率. 2.用列表法求概率的步骤: ①列表; ②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值; ③利用概率公式 3.适用条件: 如果事件中各种结果出现的可能性相等,含有两次操作(如掷骰子两次)或两个条件(如掷两个骰子)的事件.
【思考】 教师活动:教师提出问题“若上一题的情景‘同时掷两枚质地均匀的骰子’换成‘把一枚掷质均匀的骰子投两次’,所有可能的结果有变化吗?”给学生思考时间,最后给出答案,没有变化,只是列表的时候表头变为第1次,第2次即可.
|
集体回答
|
通过例题,规范学生对解题步骤的书写,让学生感受数学的严谨性.
经历试验、列表、统计、运算等活动,渗透数形结合,分类讨论、特殊到一般的思想,培养学生在具体情境中分析问题和解决问题的能力.
|
环节四 巩固新知 | 【随堂练习】 教师活动:通过Pk作答的形式,让学生独立思考,再由老师带领整理思路过程. 练习1 从1,2,−3三个数中,随机抽取两个数相乘,积是正数的概率是______.
答案:
练习2 小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( ) A.
答案:B . 追问:请用列表法写出所有可能的结果. 答案:
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为 |
Pk作答
|
进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
|
环节五 课堂小结 | 以思维导图的形式呈现本节课所讲解的内容.
|
回顾本节课所讲的内容 | 通过小结让学生进一步熟悉巩固本节课所学的知识. |
环节六 布置作业 | 巩固例题练习 教科书第138页练习1、2.
|
课后完成练习 | 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整. |
数学人教版25.1.2 概率教案配套ppt课件: 这是一份数学人教版25.1.2 概率教案配套ppt课件,共19页。PPT课件主要包含了教学目标,教学重难点,教学设计,必然事件,不可能事件,随机事件,≤PA≤1等内容,欢迎下载使用。
初中数学人教版九年级上册第二十五章 概率初步25.1 随机事件与概率25.1.2 概率教课内容ppt课件: 这是一份初中数学人教版九年级上册第二十五章 概率初步25.1 随机事件与概率25.1.2 概率教课内容ppt课件,共26页。PPT课件主要包含了学习目标,新课导入,复习回顾,新知探究,归纳总结概率的定义,正面朝上,反面朝上,随机事件,必然事件,不可能事件等内容,欢迎下载使用。
初中人教版25.1.2 概率集体备课ppt课件: 这是一份初中人教版25.1.2 概率集体备课ppt课件,共14页。