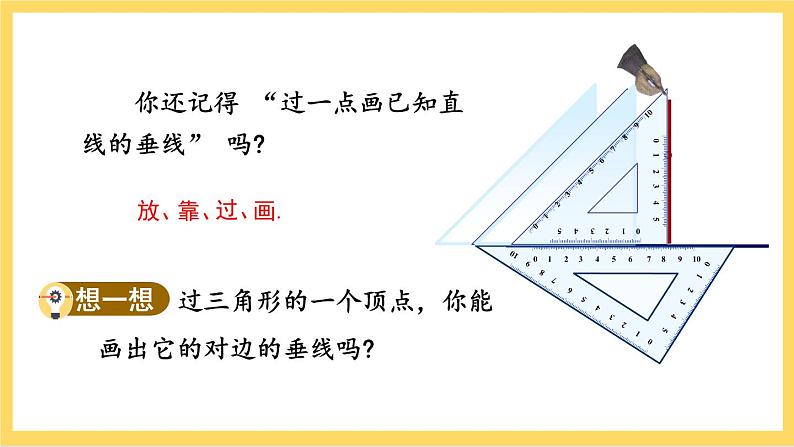
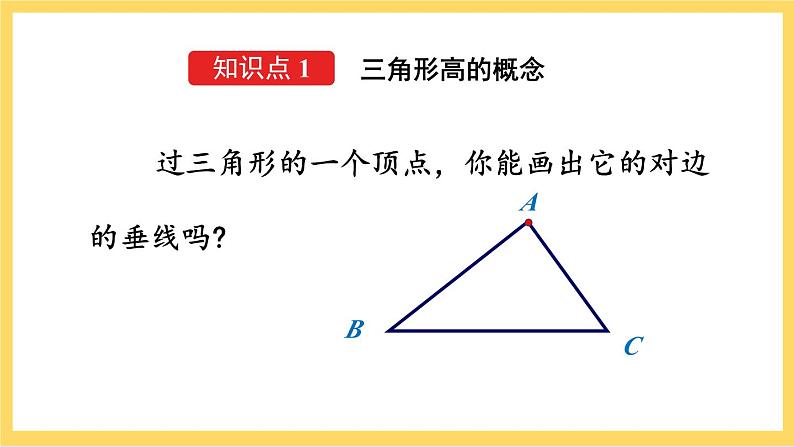
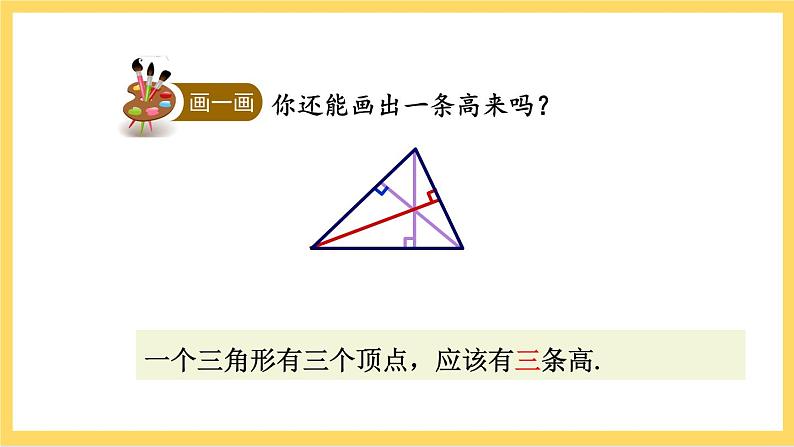
人教版数学八年级上册11.1.2《 三角形的高、中线与角平分线 》课件+教案+练习

第十一章  三角形

11.1  与三角形有关的线段
11.1.2 三角形的高、中线与角平分线

第1课时 三角形的高、中线与角平分线

1．下列说法正确的是(　　)
A．三角形三条高都在三角形内   
B．三角形三条中线相交于一点
C．三角形的三条角平分线可能在三角形内，也可能在三角形外
D．三角形的角平分线是射线

2.在△ABC中，AD为中线，BE为角平分线，则在以下等式中：①∠BAD=∠CAD；②∠ABE=∠CBE；③BD=DC；
④AE=EC．其中正确的是 (　　)
A．①②         B．③④  C．①④        D．②③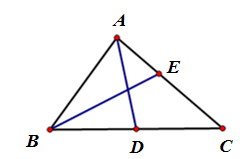

3. 如图，△ABC中∠C=90°，CD⊥AB，图中线段中可以作为△ABC的高的有(　　)
A．2条            B．3条        C．4条            D．5条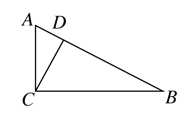

4. 下列各组图形中，哪一组图形中AD是△ABC 的BC边上的高 (    )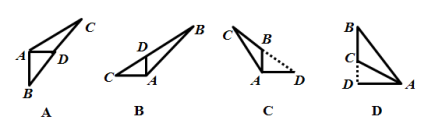

5.填空：
(1)如图①，AD，BE，CF是△ABC的三条中线，则AB= 2＿＿，BD= ＿＿，AE= ＿＿＿.
(2)如图②，AD，BE，CF是△ABC的三条角平分线，则∠1= ＿＿， ∠3=_________， ∠ACB=2______.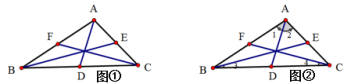

6. 在ΔABC中，CD是中线，已知BC–AC=5cm，ΔDBC的周长为25cm，求ΔADC的周长.

7. 如图，在△ABC中，AD是△ABC的高，AE是  △ABC的角平分线，已知∠BAC=82°，∠C=40°，求∠DAE的大小.

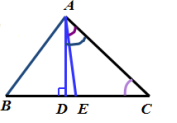
参考答案：

1.B

2.D

3.B

4.D

5.（1）AF  DC  AC   （2）∠2    ∠ABC   ∠4

6. 解：∵CD是△ABC的中线，
         ∴BD＝AD，
         ∴△DBC的周长＝BC＋BD＋CD＝25cm，
        则BD+CD＝25–BC.
         ∴△ADC的周长＝AD＋CD＋AC
                        ＝BD＋CD＋AC
                        ＝25–BC＋AC
                        ＝25–(BC–AC)＝25–5＝20cm.
    7. 解： ∵ AD是△ABC的高，∴∠ADC＝90°.

∵ ∠ADC+∠C+∠DAC=180°，

∴ ∠DAC=180°–(∠ADC+∠C )
=180°–90°–40°=50°.

∵AE是△ABC的角平分线，且∠BAC=82°，

∴∠CAE=41°，

∴∠DAE=∠DAC–∠CAE=50°–41°= 9°.