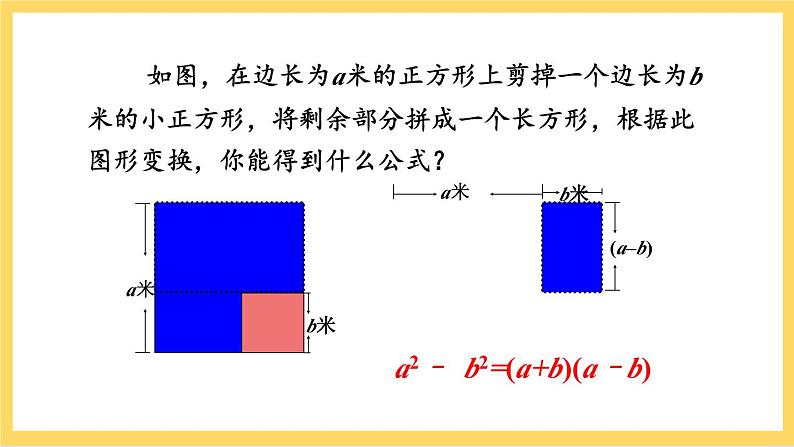
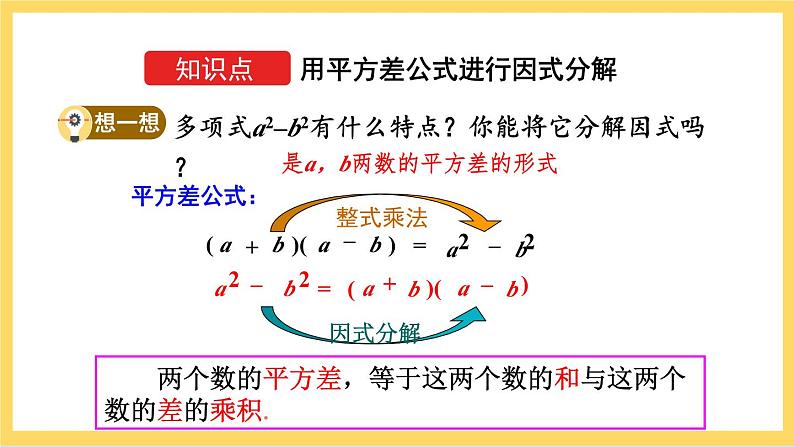
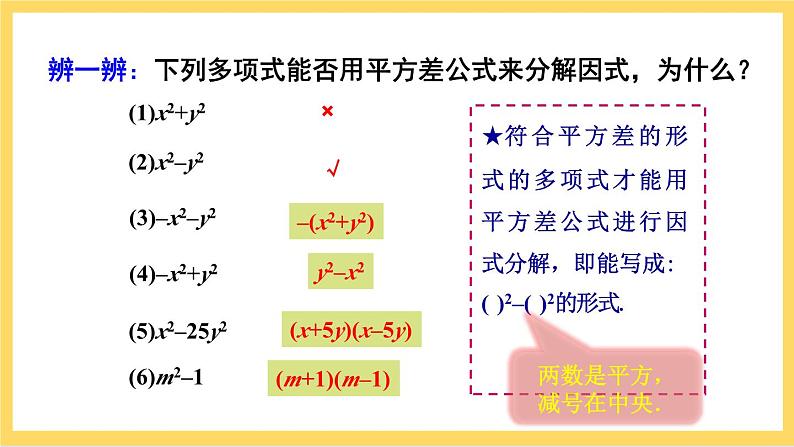
人教版八年级上册14.3.2 公式法获奖ppt课件

第十四章 整式的乘法与因式分解
14.3 因式分解

14.3.2 公式法

第1课时  运用平方差公式分解因式

1.下列多项式中能用平方差公式分解因式的是(　　)

A．a2＋(–b)2                           B．5m2–20mn

C．–x2–y2                                D．–x2＋9

2. 将多项式x–x3因式分解正确的是(　　)

A．x(x2–1)                             B．x(1–x2) 

C．x(x+1)(x–1)                D．x(1+x)(1–x)

3.若a+b=3，a–b=7，则b2–a2的值为(　　)

A．–21      B．21         C．–10             D．10

4.把下列各式分解因式：

(1)16a2–9b2=_________________; 

(2)(a+b)2–(a–b)2=_________________;  

(3) 因式分解：2x2–8=_________________;

(4) –a4+16=_________________.

5.若将(2x)n–81分解成(4x2+9)(2x+3)(2x–3)，则n的值是_____________.

6.已知4m+n=40，2m–3n=5．求(m+2n)2–(3m–n)2的值．

7.如图，在边长为6.8 cm正方形钢板上，挖去4个边长为1.6 cm的小正方形，求剩余部分的面积．

8.(1)992–1能否被100整除吗？

(2)n为整数，(2n+1)2–25能否被4整除？

参考答案：

1.D

2.D

3.A

4.(1)(4a+3b)(4a–3b);(2)4ab;(3)2(x+2)(x–2);(4)(4+a2)(2+a)(2–a)

5.4

6.解：原式=(m+2n+3m – n)(m+2n – 3m+n)

=(4m+n)(3n – 2m)

= –(4m+n)(2m – 3n)，

当4m+n=40，2m–3n=5时，

原式= – 40×5= –200．

7.解：根据题意，得

6.82–4×1.62

＝6.82– (2×1.6)2

＝6.82–3.22

＝(6.8＋3.2)(6.8 – 3.2)

＝10×3.6

＝36 (cm2)

答：剩余部分的面积为36 cm2.

8.解：(1)因为 992–1=(99+1)(99–1)=100×98，

所以992–1能被100整除.

(2)原式=(2n+1+5)(2n+1–5)

=(2n+6)(2n–4)

=2(n+3) ×2(n–2)

=4(n+3)(n–2).

所以，(2n+1)2–25能被4整除.