人教版22.2二次函数与一元二次方程精品课后测评
展开![]()
![]() 第13课 用函数观点看一元二次方程
第13课 用函数观点看一元二次方程

课程标准 |
(1)会用图象法求一元二次方程的近似解;掌握二次函数与一元二次方程的关系; (2)会求抛物线与x轴交点的坐标,掌握二次函数与不等式之间的联系; (3)经历探索验证二次函数 |

知识点01 二次函数与一元二次方程的关系
求二次函数![]() (a≠0)的图象与x轴的交点坐标,就是令y=0,求
(a≠0)的图象与x轴的交点坐标,就是令y=0,求![]() 中x的值的问题.此时二次函数就转化为一元二次方程,因此一元二次方程根的个数决定了抛物线与x轴的交点的个数,它们的关系如下表:
中x的值的问题.此时二次函数就转化为一元二次方程,因此一元二次方程根的个数决定了抛物线与x轴的交点的个数,它们的关系如下表:
判别式
| 二次函数 | 一元二次方程
| ||
图象 | 与x轴的交点坐标 | 根的情况 | ||
△>0 |
|
| 抛物线 此时称抛物线与x轴相交 | 一元二次方程
|
|
| |||
△=0 |
|
| 抛物线 | 一元二次方程
|
|
| |||
△<0 |
|
| 抛物线 | 一元二次方程
|
|
| |||
【注意】二次函数图象与x轴的交点的个数由![]() 的值来确定的.
的值来确定的.
(1) 当二次函数的图象与x轴 ,![]() ,方程有两个不相等的实根;
,方程有两个不相等的实根;
(2)当二次函数的图象与x轴 ,![]() ,方程有两个相等的实根;
,方程有两个相等的实根;
(3)当二次函数的图象与x轴 ,![]() ,方程没有实根.
,方程没有实根.
知识点02 抛物线与直线的交点问题
抛物线与x轴的两个交点的问题实质就是抛物线与直线的交点问题.我们把它延伸到求抛物线![]() (a≠0)与y轴交点和二次函数与一次函数
(a≠0)与y轴交点和二次函数与一次函数![]()
![]() 的交点问题.
的交点问题.
抛物线![]() (a≠0)与y轴的交点是(0,c).
(a≠0)与y轴的交点是(0,c).
抛物线![]() (a≠0)与一次函数
(a≠0)与一次函数![]() (k≠0)的交点个数由方程组
(k≠0)的交点个数由方程组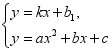 的解的个数决定.
的解的个数决定.
当方程组有两组不同的解时![]() 两函数图象 ;
两函数图象 ;
当方程组有两组相同的解时![]() 两函数图象 ;
两函数图象 ;
当方程组无解时![]() 两函数图象 .
两函数图象 .
总之,探究直线与抛物线的交点的问题,最终是讨论方程(组)的解的问题.
【注意】
求两函数图象交点的问题主要运用转化思想,即将函数的交点问题转化为求方程组解的问题或者将求方程组的解的问题转化为求抛物线与直线的交点问题.
知识点03 利用二次函数图象求一元二次方程的近似解
用图象法解一元二次方程![]() 的步骤:
的步骤:
1.作二次函数![]() 的图象,由图象确定交点个数,即方程解的个数;
的图象,由图象确定交点个数,即方程解的个数;
2. 确定一元二次方程![]() 的根的取值范围.即确定抛物线
的根的取值范围.即确定抛物线![]() 与
与
的大致范围;
3. 在(2)确定的范围内,用计算器进行探索.即在(2)确定的范围内,从大到小或从小到大依次取值,用表格的形式求出相应的y值.
4.确定一元二次方程![]() 的近似根.在(3)中最接近0的y值所对应的x值即是一元二次方
的近似根.在(3)中最接近0的y值所对应的x值即是一元二次方![]() 的近似根.
的近似根.
【注意】
求一元二次方程![]() 的近似解的方法(图象法):
的近似解的方法(图象法):
(1)直接作出函数![]() 的图象,则图象与 就是方程
的图象,则图象与 就是方程![]() 的根;
的根;
(2)先将方程变为![]() 再在同一坐标系中画出抛物线
再在同一坐标系中画出抛物线![]() 和直线
和直线![]() 图象交点的 就是方程的根;
图象交点的 就是方程的根;
(3)将方程化为![]() ,移项后得
,移项后得![]() ,设
,设![]() 和
和![]() ,在同一坐标系中画出抛物线
,在同一坐标系中画出抛物线![]() 和直线
和直线![]() 的图象,图象交点的 即为方程
的图象,图象交点的 即为方程![]() 的根.
的根.
知识点04 抛物线与x轴的两个交点之间的距离公式
当△>0时,设抛物线![]() 与x轴的两个交点为A(
与x轴的两个交点为A(![]() ,0),B(
,0),B(![]() ,0),则
,0),则![]() 、
、![]() 是一元二次方程
是一元二次方程![]() 的两个根.由根与系数的关系得
的两个根.由根与系数的关系得![]() ,
,![]() .
.
∴ ![]()
即 ![]() (△>0).
(△>0).
知识点05 抛物线与不等式的关系
二次函数![]() (a≠0)与一元二次不等式
(a≠0)与一元二次不等式![]() (a≠0)及
(a≠0)及![]() (a≠0)之间的关系如下
(a≠0)之间的关系如下![]() :
:
判别式 |
| ||
抛物线 | 不等式 | 不等式 | |
△>0 |
|
|
|
△=0 |
|
|
|
△<0 |
|
|
|
注:a<0的情况请同学们自己完成.
【注意】
抛物线![]() 在x轴上方的部分点的纵坐标都为正,所对应的x的所有值就是不等式
在x轴上方的部分点的纵坐标都为正,所对应的x的所有值就是不等式![]() 的解集;
的解集;
在x轴下方的部分点的纵坐标都为负,所对应的x的所有值就是不等式![]() 的解集.
的解集.
不等式中如果带有等号,其解集也相应带有等号.

考法01 二次函数图象与坐标轴交点
【典例1】已知二次函数y=x2+6x+c的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是( )
A.(﹣3,0) B.(3,0) C.(﹣5,0) D.(5,0)
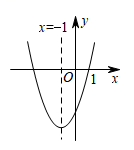
【即学即练】二次函数![]() 的部分图像如图所示,对称轴方程为
的部分图像如图所示,对称轴方程为![]() ,图像与x轴相交于点(1,0),则方程
,图像与x轴相交于点(1,0),则方程![]() 的根为( )
的根为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
【典例2】抛物线y=x2-2x+3与y轴的交点坐标是( )
A.(0,2) B.(0,3) C.(2,0) D.(3,0)
【即学即练】关于二次函数y=2x2+4x﹣1,下列说法正确的是( )
A.图象与y轴的交点坐标为(0,1) B.当x<1时,y的值随x值的增大而减小
C.图象的顶点坐标为(﹣1,﹣3) D.图象的对称轴在y轴的右侧
考法02 利用图象法求一元二次方程的解
【典例3】如图,二次函数y=ax2+bx+c的图象与x轴的右交点A(5,0),对称轴是直线x=2,当ax2+bx+c>16a时,x的取值范围是( )
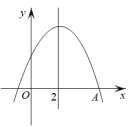
A.x<﹣1或x>5 B.﹣1<x<5 C.﹣3<x<7 D.x<﹣3或x>7
【即学即练】如图.抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集为( )
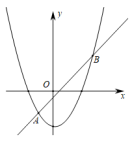
A.x>﹣1 B.x<3 C.x<﹣3或x>1 D.x>﹣1或x<3
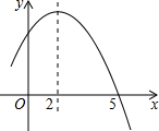
【典例4】如图,抛物线![]() 的对称轴是
的对称轴是![]() ,与x轴的一个交点为
,与x轴的一个交点为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
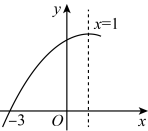
【即学即练】如图是二次函数![]() 的部分图象,由图象可知不等式
的部分图象,由图象可知不等式![]() 的解集是______.
的解集是______.
考法03 二次函数与一元二次方程的综合运用
【典例5】已知二次函数![]() (
(![]() )的图象如图所示,有下列
)的图象如图所示,有下列![]() 个结论:( )
个结论:( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
⑤若方程![]() 有四个根,则这四个根的和为
有四个根,则这四个根的和为![]() .
.
其中正确的结论有( )
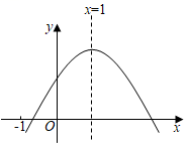
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
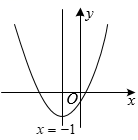
【即学即练】已知二次函数![]() 的部分图象如图所示,对称轴为直线
的部分图象如图所示,对称轴为直线![]() ,有以下结论:①
,有以下结论:①![]() ;②若t为任意实数,则有
;②若t为任意实数,则有![]() ;③当图象经过点
;③当图象经过点![]() 时,方程
时,方程![]() 的两根为
的两根为![]() ,
,![]() (
(![]() ),则
),则![]() ,其中,正确结论的个数是( )
,其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【典例6】已知抛物线y=ax2+bx+c(a,b,c是常数),a+b+c=0.下列四个结论:
①抛物线与x轴一定有两个不同的交点;
②若抛物线经过点(-1,0),则b=0;
③若b=c,则方程ax2+bx+c=0一定有根x=-2;
④点A(x1,y1),B(x1,y1)在抛物线上,若0<a<c,则当x1>x2>1时,y1>y2.
其中正确的是____________(填写序号).
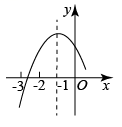
【即学即练】如图,抛物线![]() 的开口向下,对称轴为
的开口向下,对称轴为![]() ,与x轴的一个交点在(-3,0)、(-2,0)之间,其部分图像如图所示,则下列结论:①
,与x轴的一个交点在(-3,0)、(-2,0)之间,其部分图像如图所示,则下列结论:①![]() ;②
;②![]() ;③若点(
;③若点(![]() ,
,![]() )、(-
)、(-![]() ,
,![]() )、(
)、(![]() ,
,![]() )是该抛物线上的点,则
)是该抛物线上的点,则![]() ;④
;④![]() ,其中正确结论为________.
,其中正确结论为________.

题组A 基础过关练
1.抛物线![]() 与y轴的交点坐标为( )
与y轴的交点坐标为( )
A.(7,0) B.(-7,0) C.(0,7) D.(0,-7)
2.已知抛物线y=ax2+bx+c(a≠0)的顶点为(2,4),有以下结论:①当a>0时,b2-4ac>0;②当a>0时,ax2+bx+c≥4;③若点(-2,m),(3,n)在抛物线上,则m<n;④若关于x的一元二次方程ax2+bx+c=0的一根为-1,则另一根为5.其中正确的是( )
A.①② B.①④ C.②③ D.②④
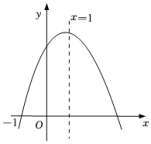
3.如图,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() .若
.若![]() ,则x的取值范围是( )
,则x的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 或
或![]()
4.二次函数y = x2 +(a + 2)x + a的图象与x轴交点的情况是( )
A.没有公共点 B.有一个公共点
C.有两个公共点 D.与a的值有关
5.已知二次函数y=ax2+bx+c的部分图象如图,则关于x的一元二次方程ax2+bx+c=0的解为( )
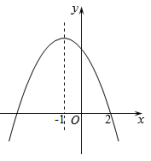
A.x1=﹣4,x2=2 B.x1=﹣3,x2=﹣1
C.x1=﹣4,x2=﹣2 D.x1=﹣2,x2=2
6.已知抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),则代数式m2﹣2m+2021的值为( )
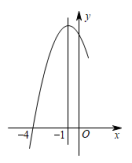
7.已知二次函数y=﹣x2﹣2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2﹣2x+m=0的解为 _____.
8.二次函数![]() (
(![]() 为常数)与
为常数)与![]() 轴的一个交点为(-1,0),则另一个交点为___________.
轴的一个交点为(-1,0),则另一个交点为___________.
9.抛物线![]() 与
与![]() 轴交于点(0,3).
轴交于点(0,3).
(1)求![]() 的值及抛物线与
的值及抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(2)![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴下方?
轴下方?
(3)![]() 取什么值时,
取什么值时,![]() 的值随着
的值随着![]() 的增大而增大?
的增大而增大?
10.已知二次函数的图象经过点![]() 和点
和点![]() ,且有最小值为
,且有最小值为![]() .
.
(1)求这个函数的解析式、函数的开口方向、对称轴;
(2)当![]() 时,x的取值范围.
时,x的取值范围.
题组B 能力提升练
1.已知函数![]() 的图象如图,那么关于x的方程
的图象如图,那么关于x的方程![]() 的根的情况是( )
的根的情况是( )
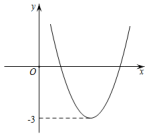
A.无实数根 B.有两个相等实数根
C.有两个同号不等实数根 D.有两个异号实数根
2.如表中列出的是二次函数y=a![]() +bx+c中x与y的几组对应值:
+bx+c中x与y的几组对应值:
x | … | ﹣2 | 0 | 1 | 3 | … |
y | … | 6 | ﹣4 | ﹣6 | ﹣4 | … |
下列各选项中,正确的是( )A.这个函数的图象开口向下
B.这个函数的图象与x轴有两个交点,且都在y轴同侧
C.当x>1时,y的值随x值的增大而增大
D.方程a![]() +(b+2)x+c=﹣4的解为
+(b+2)x+c=﹣4的解为![]() =0,
=0,![]() =1
=1
3.已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是( )
A.k>-![]() 且k≠0 B.k>-
且k≠0 B.k>-![]()
C.k≥-![]() 且k≠0 D.k≥-
且k≠0 D.k≥-![]()
4.若抛物线y=![]() 与x轴交于点A,B,与y轴交于点C,则△ABC的面积为( )
与x轴交于点A,B,与y轴交于点C,则△ABC的面积为( )
A.24 B.36 C.48 D.96
5.如图,若二次函数![]() 图象的对称轴为
图象的对称轴为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,则①二次函数的最大值为
,则①二次函数的最大值为![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() ;其中正确的个数是( )
;其中正确的个数是( )
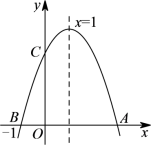
A.1 B.2 C.3 D.4
6.二次函数y=ax2+bx的图像如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
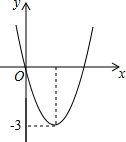
A.﹣3 B.﹣2 C.2 D.3
7.已知抛物线![]() 与x轴的一个交点为
与x轴的一个交点为![]() ,则代数式
,则代数式![]() _____________.
_____________.
8.如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为____.
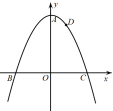
9.已知二次函数y=![]() -(m+2)x+2m-1
-(m+2)x+2m-1
(1)求证:不论m取何值,该函数图象与x轴总有两个公共点;
(2)若该函数的图象与y轴交于点(0,3),求当0<x<5时,求y的取值范围.
10.如图,二次函数![]() 的图象与
的图象与![]() 轴的一个交点为
轴的一个交点为![]() ,另一个交点为
,另一个交点为![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .
.
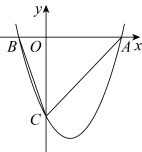
(1)求二次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)该二次函数图象上是否存在点![]() ,使
,使![]() 与
与![]() 的面积相等?若存在,请求出
的面积相等?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
题组C 培优拔尖练
1.若![]() ,
,![]() 是方程
是方程![]() (c为常数)两个不相等的实数根,且满足
(c为常数)两个不相等的实数根,且满足![]() ,则c的取值范围是( )
,则c的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,二次函数y=ax2+bx+c(a为常数,且a≠0)的图象过点(﹣1,0),对称轴为直线x=1,且2<c<3,则下列结论正确的是( )
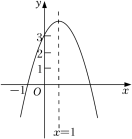
A.abc>0 B.3a+c>0
C.a2m2+abm≤a2+ab(m为任意实数) D.﹣1<a<﹣![]()
3.在平面直角坐标系中,已知函数![]() ,
,![]() ,
,![]() ,其中a=2,b、c都是正实数,且满足b2=ac.设y1,y2,y3的图象与x轴的交点个数分别为M1,M2,M3,则下列结论错误的是( )
,其中a=2,b、c都是正实数,且满足b2=ac.设y1,y2,y3的图象与x轴的交点个数分别为M1,M2,M3,则下列结论错误的是( )
A.若M1=1,M2=1,则M3=2 B.若M1=1,M2=1,则M3=1
C.若M1=1,M2=0,则M3=0或1或2 D.若M1=1,M2=2,则M3=2
4.已知抛物线![]() 与
与![]() 轴的两个交点之间的距离为6,对称轴为
轴的两个交点之间的距离为6,对称轴为![]() ,则抛物线的顶点
,则抛物线的顶点![]() 关于
关于![]() 轴对称的点
轴对称的点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:
①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的为( )
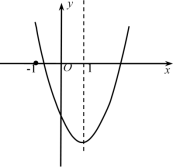
A.①② B.②③④ C.①②④ D.①②③④
6.下表记录了二次函数![]() 中两个变量x与y的6组对应值,其中
中两个变量x与y的6组对应值,其中![]() .
.
x | … |
|
|
| 1 |
| 3 | … |
y | … | m | 0 | 2 | 0 | n | m | … |
根据表中信息,当![]() 时,直线
时,直线![]() 与该二次函数图像有两个公共点,则k的取值范围为( ).
与该二次函数图像有两个公共点,则k的取值范围为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.若函数![]() 的图象与坐标轴有两个不同的交点,则m的值为____.
的图象与坐标轴有两个不同的交点,则m的值为____.
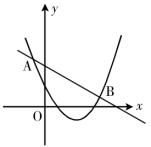
8.已知二次函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() 和
和![]() ,如图所示,则使不等式
,如图所示,则使不等式![]() 成立的
成立的![]() 的取值范围是_____________.
的取值范围是_____________.
9.平面直角坐标系xOy中,已知抛物线y=![]() +bx+c经过(﹣1,
+bx+c经过(﹣1,![]() +2m+1)、(0,
+2m+1)、(0,![]() +2m+2)两点,其中m为常数.
+2m+2)两点,其中m为常数.
(1)求b的值,并用含m的代数式表示c;
(2)若抛物线y=![]() +bx+c与x轴有公共点,求m的值;
+bx+c与x轴有公共点,求m的值;
(3)设(a,![]() )、(a+2,
)、(a+2,![]() )是抛物线y=
)是抛物线y=![]() +bx+c上的两点,请比较
+bx+c上的两点,请比较![]() ﹣
﹣![]() 与0的大小,并说明理由.
与0的大小,并说明理由.
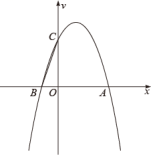
10.如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .已知
.已知![]() ,该抛物线的对称轴为直线
,该抛物线的对称轴为直线![]() .
.
(1)求该抛物线的函数表达式;
(2)求点![]() 、
、![]() 的坐标;
的坐标;
(3)将线段![]() 平移,使得平移后线段的一个端点在这条抛物线上,另一个端点在
平移,使得平移后线段的一个端点在这条抛物线上,另一个端点在![]() 轴上,若将点
轴上,若将点![]() 、
、![]() 平移后的对应点分别记为点
平移后的对应点分别记为点![]() 、
、![]() ,求以
,求以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
初中数学人教版九年级上册21.1 一元二次方程精品精练: 这是一份初中数学人教版九年级上册21.1 一元二次方程精品精练,文件包含人教版九年级数学上册同步精品讲义第13课用函数观点看一元二次方程教师版doc、人教版九年级数学上册同步精品讲义第13课用函数观点看一元二次方程原卷版doc等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
数学22.1 二次函数的图象和性质综合与测试练习: 这是一份数学22.1 二次函数的图象和性质综合与测试练习,共15页。试卷主要包含了二次函数与一元二次方程的关系,抛物线与不等式的关系等内容,欢迎下载使用。
数学九年级上册21.1 一元二次方程达标测试: 这是一份数学九年级上册21.1 一元二次方程达标测试,共25页。