





初中数学人教版九年级上册24.4 弧长及扇形的面积精品同步达标检测题
展开![]()
![]() 第25课 弧长和扇形面积、圆锥的侧面展开图
第25课 弧长和扇形面积、圆锥的侧面展开图
课程标准 |
(1)通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长 (3)能准确计算组合图形的面积. |
知识点01 弧长公式
半径为R的圆中:
360°的圆心角所对的弧长(圆的周长)公式: ![]()
n°的圆心角所对的圆的弧长公式: ![]() (弧是圆的一部分);
(弧是圆的一部分);
【注意】
(1)对于弧长公式,关键是要理解1°的圆心角所对的弧长是圆周长的 ,即![]()
![]() = ;
= ;
(2)公式中的n表示1°圆心角的倍数,故n和180都不带单位,R为弧所在圆的半径;
(3)弧长公式所涉及的三个量:弧长、圆心角度数、弧所在圆的半径,知道其中的两个量就可以求出第三个量.
知识点02 扇形面积公式
1.扇形的定义
由组成 ![]()
![]()
![]() 所围成的图形叫做扇形.
所围成的图形叫做扇形.
2.扇形面积公式
半径为R的圆中:
360°的圆心角所对的扇形面积(圆面积)公式: ![]()
n°的圆心角所对的扇形面积公式:S扇形= ![]()
【注意】
(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的 ,即![]()
![]() ;
;
(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.
(3)扇形面积公式S扇形![]() ,可根据题目条件灵活选择使用,它与三角形面积公式
,可根据题目条件灵活选择使用,它与三角形面积公式![]() 有点类似,可类比记忆;
有点类似,可类比记忆;
(4)扇形两个面积公式之间的联系:S扇形= .
知识点03 圆锥的侧面积和全面积
连接圆锥 和 ![]() 的线段叫做圆锥的母线.
的线段叫做圆锥的母线.
圆锥的母线长为l,底面半径为r,侧面展开图中的扇形圆心角为n°,则
圆锥的侧面积 ,
圆锥的全面积:S全=S侧+S底= ![]() .
.
【注意】
扇形的半径就是圆锥的 ,扇形的弧长就是圆锥底面圆的 .因此,要求圆锥的侧面积就是求展开图扇形面积,全面积是由侧面积和底面圆的面积组成的.
考法01 弧长和扇形的有关计算
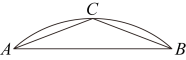
【典例1】如图,点C为![]() 的中点,∠ABC=22.5°,AB
的中点,∠ABC=22.5°,AB![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
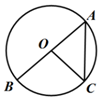
【即学即练】如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则![]() 的长为( )
的长为( )
A.![]() π B.
π B.![]() π C.
π C.![]() π D.
π D.![]() π
π
【典例2】半径为2的圆中,扇形MON的圆心角为150°,则这个扇形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【即学即练】已知圆锥的母线长是5cm,侧面积是20πcm2,则这个圆锥底面圆的半径是( )
A.1.5cm B.3cm C.4cm D.6cm
考法02 圆锥面积的计算
【典例3】一个圆锥的母线长为6,侧面展开图是半圆,则圆锥的侧面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【即学即练】已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )
A.96πcm2 B.48πcm2 C.33πcm2 D.24πcm2
【典例4】如图,圆锥的底面圆半径r为5cm,高h为12cm,则圆锥的侧面积为( )
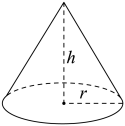
A.![]() cm2 B.
cm2 B.![]() cm2 C.
cm2 C.![]() cm2 D.
cm2 D.![]() cm2
cm2
【即学即练】如图,圆锥的底面半径OB=3cm,高OC=4cm.则这个圆锥的侧面积是( )
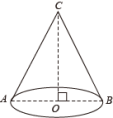
A.15cm2 B.12πcm2 C.15πcm2 D.20πcm2
考法03 组合图形面积的计算
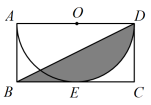
【典例5】如图,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径的半圆
为直径的半圆![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
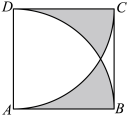
【即学即练】如图,正方形![]() 的边
的边![]() ,
,![]() 和
和![]() 都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
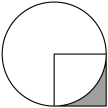
【典例6】正方形的面积是33平方米,则阴影部分面积是( )
A.33﹣![]() π B.33﹣
π B.33﹣![]() π C.
π C.![]() π D.33﹣
π D.33﹣![]() π
π
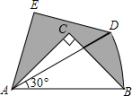
【即学即练】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为![]() ,则图中阴影部分的面积是( )(提示:圆心角为n°的扇形的面积为
,则图中阴影部分的面积是( )(提示:圆心角为n°的扇形的面积为![]() ,R为扇形所在的圆的半径)
,R为扇形所在的圆的半径)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
题组A 基础过关练
1.已知一个扇形的圆心角为120°,半径是6cm,则这个扇形的弧长是( )
A.8π B.6π C.4π D.2π
2.一个圆锥侧面展开图的扇形的弧长为![]() ,则这个圆锥底面圆的半径为( )
,则这个圆锥底面圆的半径为( )
A.6 B.12 C.24 D.2
3.已知,如图,⊙O的半径为6,正六边形ABCDEF与⊙O相切于点C、F,则![]() 的长度是( )
的长度是( )
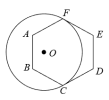
A.2π B.3π C.4π D.5π
4.如图,将线段OA绕点O逆时针旋转45°,得到线段OB.若OA=8,则点A经过的路径长度为( )
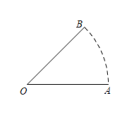
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
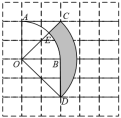
5.如图所示,边长为1的正方形网格中,O,A,B,C,D是网格线交点,若![]() 与
与![]() 所在圆的圆心都为点O,那么阴影部分的面积为( )
所在圆的圆心都为点O,那么阴影部分的面积为( )
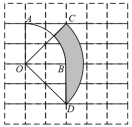
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
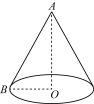
6.如图所示,某盏路灯照射的空间可以看成如图所示的圆锥,它的高![]() 米,底面半径
米,底面半径![]() 米,则圆锥的侧面积是多少平方米(结果保留
米,则圆锥的侧面积是多少平方米(结果保留![]() )( )
)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知扇形的半径为 ![]() 圆心角为
圆心角为 ![]() 则此扇形的面积是_____________.
则此扇形的面积是_____________.
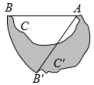
8.如图,将以线段AB和曲线BCA围成的图形ABCA绕点A逆时针旋转45°至图形AB′C′A的位置,若AB=8,则图中阴影部分的面积为______.
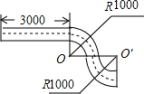
9.如图是一段弯形管道,其中,![]() ,中心线的两条圆弧半径都为
,中心线的两条圆弧半径都为![]() .求图中管道的展直长度.
.求图中管道的展直长度.
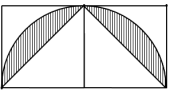
10.下列每个正方形的边长为2,求下图中阴影部分的面积.
题组B 能力提升练
1.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
2.Rt△ABC中,∠C=90°,AC=3,BC=4.把它沿AC所在直线旋转一周,所得几何体的全面积为( )
A.16π B.20π C.36π D.40π
3.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( )

A.![]() B.
B.![]() C.4 D.
C.4 D.![]()
4.如图,六边形ABCDEF是半径为2的圆的内接正六边形,则阴影部分的面积为( )
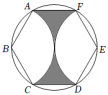
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,以点C为圆心,CA的长为半径画弧,交AB于点D,则弧AD的长为( )
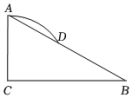
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.2
D.2![]()
6.一个垃圾填埋场,它在地面上的形状为长![]() ,宽
,宽![]() 的矩形,有污水从该矩形的四周边界向外渗透了
的矩形,有污水从该矩形的四周边界向外渗透了![]() ,则该垃圾填埋场外围受污染土地的面积为( )
,则该垃圾填埋场外围受污染土地的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若一个扇形的半径是9cm,且它的弧长是6πcm,则此扇形的圆心角等于 _____.
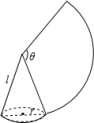
8.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥母线l=6,扇形的圆心角![]() ,则该圆锥的底面圆的半径r长为______.
,则该圆锥的底面圆的半径r长为______.
9.如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?

10.用铁皮制作圆锥形容器盖,其尺寸要求如图所示 .
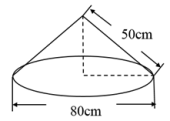
(1)求圆锥的高;
(2)求所需铁皮的面积![]() (结果保留
(结果保留![]() ).
).
题组C 培优拔尖练
1.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是( )
A.120° B.150° C.60° D.100°
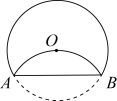
2.如图,将⊙O沿弦AB折叠,![]() 恰好经过圆心O,若⊙O的半径为3,则
恰好经过圆心O,若⊙O的半径为3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
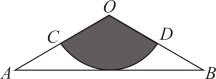
3.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆的半径为( )cm.
A.15 B.30 C.45 D.30π
4.如图,边长为![]() 的正方形
的正方形![]() 内接于
内接于![]() ,
,![]() ,
,![]() 分别与
分别与![]() 相切于点
相切于点![]() 和点
和点![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
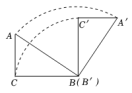
5.如图,在Rt△ABC中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点B顺时针旋转90°得到
绕点B顺时针旋转90°得到![]() .在此旋转过程中
.在此旋转过程中![]() 所扫过的面积为( )
所扫过的面积为( )
A.25π+24 B.5π+24 C.25π D.5π
6.蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
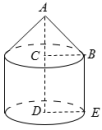
A.圆柱的底面积为4πm2 B.圆柱的侧面积为10πm2
C.圆锥的母线AB长为2.25m D.圆锥的侧面积为5πm2
7.扇形的圆心角是120°,面积是3π cm²,则扇形的弧长是___________cm,将此扇形卷成一个圆锥,则底面圆的半径为_________cm.
8.如图,![]() ,
,![]() ,
,![]() 两两不相交,且半径都等于
两两不相交,且半径都等于![]() ,则图中三个扇形(即阴影部分)的面积之和为______.(结果保留
,则图中三个扇形(即阴影部分)的面积之和为______.(结果保留![]() )
)
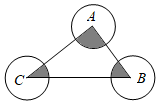
9.将图中的破轮子复原,已知弧上三点A,B,C.
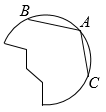
(1)画出该轮的圆心;
(2)若![]() 是等腰三角形,底边
是等腰三角形,底边![]() cm,腰AB=10cm,求弧BC的长.
cm,腰AB=10cm,求弧BC的长.
10.如图,点![]() 都在
都在![]() 上,过点C作AC//BD交
上,过点C作AC//BD交![]() 延长线于点A,连接
延长线于点A,连接![]() ,且
,且![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)求![]() 的半径长.
的半径长.
(3)求由弦![]() 与弧
与弧![]() 所围成的阴影部分的面积(结果保留
所围成的阴影部分的面积(结果保留![]() ).
).













